ztm2 (850176), страница 4

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 4)

е го представляют разделённым на меньших тел (см. рис.6), веса и положения ( ) центров тяжести которых известны; тогда, в соответствии с законом Вариньона:

, где

Рисунок 14.3

- вес исходного тела.

Из 14.13 видно, что положения центров тяжести однородных тел зависят от геометрических форм, но не от разновидностей материалов. В связи с этим, оперируют также понятиями: «центр тяжести объёма», «центр тяжести плоской фигуры», «центр тяжести линии». Чтобы отличать одно от другого в формулах 14.13 вместо можно условиться писать другие буквы: в первом случае - , во втором - , в третьем - . Этот результат легко видится, если веса начать выражать через удельный вес ( ), или через вес единицы площади плоской фигуры, или через вес единицы длины линии. Например, и ясно, что , как величина, не зависящая от номера частицы тела, из уравнения уйдёт – окажется и в числителе, и в знаменателе.

Из 14.13 рекомендуем самостоятельно получить и такой результат:

ц

О центре тяжести треугольника

ентр тяжести однородного тела располо-жен в плоскости симметрии, на оси симметрии, в точке симметрии (если таковые имеются).

Переходим к рассмотрению основных приёмов, применяемых при определении центров тяжести однородных тел простых конфигураций.

Ц ентр тяжести однородного треугольника находится на пересечении его медиан.

Сформулированный результат можно получить следующими рассуждениями.-

Р

Рисунок 14.4

азбиваем треугольник на бесконечно большое число бесконечно узких полосок, параллельных основанию АВ. ЕF – одна из них, -тая (см. рис. 14.4).

54

М

14.17

едиана ДG пересекает -тую полоску посередине (в точке ). В соответствии с 14.14 ордината её центра тяжести ( ) равна нулю. Таким образом, распределённая по поверхности треугольника система сил тяжести сводится к тяжёлой линии - к медиане ДG.

Т

14.18

.к. для любой из расматриваемых элементарных полосок , то на основании 14.13 заключаем: центр тяжести треугольника расположен на медиане ДG.

Аналогично приходим к выводу о том, что центр тяжести треугольника расположен и на медиане АК.

Н

14.19

о тело имеет лишь один центр тяжести. Следовательно, он расположен на пересечении DG и AK.

О

О центре тяжести дуги окружности

14.20

сталось лишь напомнить (из элементарной геометрии): точка пересечения медиан делит каждую из них на два отрезка, один из которых (примыкающий к вершине треугольника) в два раза больше второго.

Ц

14.16

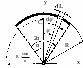ентр тяжести однородной дуги окружности (см. рис.14.5) расположен на её оси симметрии и отстоит от центра этой окружности на расстоянии

где - радиус окружности;

- половина центрального угла, на который дуга опирается.

Р

Рисунок 14.5

езультат 14.16 можно получить следующим образом.-

Ось (см. рис.14.5) направляем так, чтобы она оказалась осью симметрии рассматриваемой дуги. Тогда (в соответствии с 14.14), .

Длина дуги: .

Представим её состоящей из бесконечно большого числа бесконечно малых дуг, одна из которых (длиной ) изображена на рисунке. Тогда:

.

Ниже приведенные результаты 14.17-14.20 получите самостоятельно:

55

ц

О центре тяжести кругового сектора

ентр тяжести однородного кругового сектора отстоит от центра круга на расстоянии

, где

- радиус круга; - половина секторного угла;

у

Рисунок 14.6

однородной полусферы (рис.14.7) центр тяжести отстоит от её основания (от экваториальной окружности) на расстоянии, равном половине радиуса;

у однородного полушара (см. рис.14.8) центр тяжести отстоит от основания-круга на растоянии трёх восьмых радиуса.

ц ентр тяжести однородной пирамиды (и конуса) расположен на отрезке, соединяющем центр тяжести основания с вершиной и отсто-ит от вершины на расстоянии, равном трём четвертям этого отрезка.

О центре тяжести полусферы

О центре тяжести полушара

Рисунок 14.7

Рисунок 14.8

Куб. На нём пирамида

П РИМЕР 14.1.- Вычислить координаты центра тяжести тела по рис.14.9.

м – длина ребра куба. .

Решение.- - Центр тяжести расположен на оси симметрии (на ) - м.

Рисунок 14.9

м.

56

1

15.4

5. Равновесие тел

15.1. Уравнения равновесия

Как уже было определено, для уравновешенной системы и ; причём, главный момент равен нулю независимо от центра, относительно которого он вычислялся.

С другой стороны:

;

Замечание: как здесь, так и в дальнейшем, с целью сокращения записей пределы суммирования будем опускать.

Т
аким образом, для находящегося в равновесии тела:

П
одкоренные выражения состоят из сумм квадратов действительных чисел и поэтому ясно, что равенства а могут иметь место лишь в случаях:

15.1

, , ;

15.2

15.5

, , .

М

15.6

атематические выражения 15.1 называют уравнениями проекций, 15.2– уравнениями моментов.

Совокупность уравнений проекций и уравнений моментов называют уравнениями равновесия (для произвольной системы сил, стандартная форма).

У

15.7

равнения 1 и 2 словами описывать принято примерно так:

у

15.8

равнения проекций - «сумма проекций (на такую-то ось, например на ) всех приложенных (к такому-то телу) сил равна нулю»;

уравнения моментов - «сумма моментов относительно оси (такой-то, например относительно оси ) всех приложенных (к такому-то телу) сил равна нулю».

У

15.9

равнения равновесия обычно составляют с целью определения неизвестных сил. При этом, полезно иметь ввиду:

н

15.3

15.10

еизвестная сила, расположенная перпендикулярно оси, не входит в уравнение проекций на эту ось;

57

н еизвестная сила не входит в уравнение моментов, если линия её действия параллельна, либо пересекает ось, относительно которой момент вычисляется.

Одна тройка взаимно перпендикулярных осей, особенно наугад взятая, чаще всего даёт сложную в решении систему уравнений (даёт нераспадающуюся систему 6 уравнений). Но нет запрета дополнить её уравнениями равновесия, составленными для других систем координат, отличающихся от первой и учитывающих свойства 15.3-15.4.

В расширенной указанным способом системе уравнений обычно обнаруживаются уравнения с одной неизвестной, либо обнаруживаются подсистемы двух уравнений с двумя неизвестными, что существенно облегчает решение конкретных задач.

Возникают интересные, с точки зрения облегчения расчётов, вопросы:

• к акое максимальное количество неизвестных позволяют определить составленные в большом количестве уравнения равновесия?

• к

  а

  акие из них целесообразнее всего использовать для определения неизвестных?

Отвечать на поставленные вопросы можно путём анализа ранга матрицы, составленной по коэффициентам уравнений равновесия. Подробнее с этим вопросом можно ознакомиться в учебном пособии: «Игнатищев Р.М. Теоретическая механика. Статика.- Могилёв: ММИ, 1978.- С.50-56». Здесь же ограничимся приведением лишь основных результатов этого анализа.

При произвольной пространственной системе сил:

ч исло линейно независимых уравнений равновесия, составленных для одного тела, не может быть больше шести и, поэтому, если число входящих в уравнения неизвестных превышает число 6, то все их определить не удасться, сколько бы уравнений вы не составили;

ч исло линейно независимых уравнений проекций для одного тела не может быть больше трёх;

е сли оси, относительно которых записывают уравнения моментов, пересекаются в одной точке, то число линейно независимых уравнений моментов не может быть больше трёх;

в случаях 15.6 и 15.7 перпендикулярность осей не обязательна;

в случае параллельных осей можно составить лишь 3 линейно независимых уравнений моментов; причём, эти оси нельзя располагать в одной плоскости (в противном случае линейно независимых уравнений моментов окажется лишь 2);

в случае двух систем координат с несовпадающими плоскостями, параллельность допустима, линейно независимыми оказываются все шесть уравнений моментов.

58

Д

15.11

ля тел, находящихся под действием системы сил, линии действия которых совпадают, может быть составлено лишь одно уравнение равновесия; проще всего - , где - ось, совпадающая с линией действия названной системы сил.

Другие уравнения в своих первоначальных написаниях окажутся сложнее, но после соответствующих преобразований будут упрощены и доведены до рекомендованных; но зачем эти дополнительно-преобразовательные операции?

Д

15.12

ля тела, находящегося под действием плоской сходящейся систе-мы сил, может быть составлено лишь два линейно независимых уравнений равновесия; проще всего и , где и - любые непараллельные (не обязательно взаимно перпендикулярные) оси, расположенные в плоскости действия сил.

Д

15.13

15.16

ля тела, находящегося под действием пространственной сходя-щейся системы сил, можно составить лишь три линейно независи-мых уравнений равновесия; проще всего , , , где - произвольные оси, которые при параллельном своём переносе в одну точку образуют трёхгранник.

Часто выгодными (по соображениям получения более простых выражений) являются не взаимно перпендикулярные оси.

Д

15.14

15.17

ля тела, находящегося под действием пространственной системы параллельных сил, можно составить не более трёх линейно независимых уравнений равновесия; проще всего , , , где и - непараллельные друг другу оси, расположенные в плоскости, перпендикулярной линиям действия сил; ось параллельна линиям действия сил.

К

15.18

огда рассматривают плоские системы сил (в учебном процессе с ними чаще всего и приходится иметь дело), то пользуются понятием «момент силы относительно точки ». Обозначения: , или (момент -той силы относительно точки А).

П

15.19

од моментом силы относительно точки понимают взятое со знаком «+» или «-» произведение модуля силы на кратчайшее расстояние ( ) от взятой точки А до линии действия силы, т.е.

15.15

.

Характеристики

Список файлов книги