ztm14 (850188)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

, т.е.

.

Иначе: ,

где ,

.

В соответствии с теоремой Пифагора: .

Поэтому:

, т.е.

б

, где

.

Известно, что направляющие косинусы связаны между собою зависимостью

. Откуда:

, ,

.

Приводим к нужному виду :

28.10а

.

237

Н

в

аправляющие углы не зависят от номеров частиц.

По этой причине выносим за знаки интегралов квадраты косинусов и, в соответствии с понятиями осевых моментов инерции (см. 28.1), получаем:

г

.

Теперь, учитывая (в), приводим к нужному виду :

и далее, в соответствии с понятиями центробежных моментов инерции (см. 28.2):

д

.

Справедливость формулы 28.9 доказана – это видно, если в верхнюю строчку выражений (б) подставить (г) и (д).

28.7. Понятие об эллипсоидах инерции, главных и главных центральных осях инерции

С точки зрения машиностроительных технологий несложно ось вращения относительно тела расположить так, как задаст конструктор. Но произвольно задавать эту ось нельзя, ибо вместо спокойного, бесшумного вращения тела, можно получить грохочащее устройство с недопустимыми уровнями шума, вибраций при громадных динамических нагрузках на детали.

В следующем разделе будет показано, что для предупреждения появления описанных негативных механических проявлений нужно, в частности, оси вращения принимать такими, чтобы соответствующие центробежные моменты инерции оказывались равными нулю.

Но достижимо ли это в принципе? И если достижимо, то как делать?

Путь к решению этих вопросов лежит через понятие «эллипсоид инерции».

Вводим семёрку изображений моментов инерции:

где

- осевые и центробежные моменты инерции;

238

п

28.10

ри этом, обозначения соответствуют предыдущему подразделу;

- масштабный коэффициент, обеспечивающий изображениям линейные размеры (например в миллиметрах); - аналог тем масштабным коэффициентам, которые применяют для изображения на бумаге сил, скоростей, ускорений и т.д.

Итак, изображения моментов инерции – это отрезки, по значению длин которых можно судить о значениях самих моментов инерции. Например

и можно сказать: чем больше длина отрезка , тем меньше ; при ; и т.д.

Оперирование моментами инерции не непосредственно, а через их изображения, удобно тем, что позволяет анализ свести к известной математической модели.

И

К понятию

«эллипсоид инерции»

Рисунок 28.9

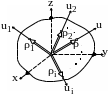зображение момента инерции представляем в виде вектора , где - орт оси , произвольно ориентированной (см. на рис.9 и т.д.) и проходящей через начало системы . Ясно, поэтому, что связанный (начинаю-щийся в точке ) вектор , как и ось , имеет переменную ориентацию, определяемую направляющими углами . Координаты его конца обозначаем .

Выясним, какую поверхность в системе отображает конец вектора ?

С целью ответа на поставленный вопрос в уравнение 28.9 вместо моментов инерции подставляем их изображения (подчинённые условиям 28.10а). При этом учитываем, что:

.

Получается:

239

.

12

И

Эллипсоид инерции

з аналитической геомет-рии известно, что уравнение 28.10 отображает фигуру, называемую эллипсоидом. Применительно к рассматриваемому случаю - «эллипсоидом инерции при точке тела» (см. рис.28.10).

и - полуоси эллипсоида. В общем случае они различны по длине. Частные случаи: сфера ( );

с

Рис.28.10

фероид (одинаковы две полуоси - , или , или ).

- называют осями эллипсоида. Из аналитической геометрии известно: если (ось системы отсчёта совпадает с осью эллипсоида), то уравнение 28.10 имеет вид:

,

т.е. в нём .

По геометрическому смыслу отображают точки поверхности эллипсоида и не могут равняться нулю. Значит равны бесконечности находящиеся в знаменателях и ; поэтому (что видно из 28.10а), равны нулям центробежные моменты инерции и . Итак:

28.11

для тела любой формы, в любой его точке имеется свой эллипсоид инерции; его оси называют главными осями инерции;

28.12

центробежные моменты инерции, включающие в свои обозначения главную ось, равны нулю -

пусть, например, главной осью является ; тогда , где и - оси, дополняющие до декартовой прямоугольной системы координат;

240

28.13

главную ось инерции, проходящую через центр тяжести тела, называют главной центральной осью инерции;

28.14

тело любой формы имеет, как минимум, тройку взаимно перпендикулярных главных центральных осей инерции.

Руководствуясь понятиями «главная ось инерции», «центробежный момент инерции», «ось материальной симметрии», «плоскость материальной симметрии» и «интеграл» самостоятельно докажите справедливость результатов 28.15 и 28.15.

28.15

ось ось материальной симметрии тела, если имеется, одновременно является и его главной центральной осью инерции;

28.16

если тело имеет плоскость материальной симметрии (например, кузов вагона), то любая перпендикулярная ей ось является главной осью инерции этого тела.

К примеру 28.3

П РИМЕР 28.3.- Момент инерции диска относительно оси точечно касающейся цилиндрической его поверхности

Дано. – Сплошной однородный диск, радиуса и массой . Моменты инерции относительно осей (см. рис.28.11) считать известными. Оси и параллельны, .

Т

Рисунок.28.11

ребуется. - Определить момент инерции диска относительно оси -

Решение.- являются осями симметрии диска. Значит и формула 28.9 принимает вид:

, т.е.

.

Теперь используем формулу связи между моментами инерции относительно параллельных осей: .

241

П

К примеру 28.4

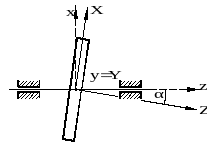РИМЕР 28.4.- Определение центробежных моментов инерции диска, наклонённого к оси вращения

Дано. – Сплошной однородный диск ради-уса и массой . Из-за погрешностей изготовления и монтажа его ось вращения оказалась смещённой на угол относительно центральной, перпендику-лярной торцам, оси (см. рис.28.12).

Т

Рисунок 28.12

ребуется. - Определить центробежные моменты инерции диска, включающие в свои обозначения ось -

Решение.- Связываем с диском две системы координат и , так чтобы оси первой системы оказались главными центральными осями инерции диска, а совпадала с .

Т.к. ось - главная ось инерции, то .

Переходим к определению . Для этого вначале необходимо определить и . Их определим по формуле 28.9. Учитываем отсутствие второй тройки слагаемых (т.к. - трёхгранник главных осей):

;

.

Теперь за базовую систему отсчёта принимаем и, воспользовавшись той же формулой 28.9, определяем искомый центробежный момент инерции :

.

Откуда:

Учитывая уже вычисленные в этом примере , и то, что

(см. подраздел 4), получаем: .

242

29. Закон об изменении кинетического момента

и основы динамики вращательно, плоско

и сферически движущихся тел

29.1. Понятие «кинетический момент» и общие формулы для его вычисления

Н

К понятию «момент количества движения материальной точки»

а рис.1: - траектория, - масса,

- скорость материальной точки относительно системы отсчёта .

В

29.1

еличину , определяемую математическим выражением

,

называют моментом количества движения материальной точки относительно центра .

В

Рисунок 29.1

математическом плане выражение 29.1 идентично изученному в статике

.

По этой причине методы, применявшиеся при использовании формулы , полностью переносятся на . В частности, проекции на оси системы ( ) называют моментами количества движения материальной точки относительно осей , и для их вычисления удобно применять тот же «способ перестановки индексов» -

.

Пусть имеем механическую систему, состоящую из материальных точек.

Величину проще называют кинетическим моментом механической системы относительно центра , или, по аналогии с главным моментом, - главным моментом количеств движений относительно центра .

В

29.3

торое название длинное. Поэтому будем пользоваться, в основном, термином «кинетический момент».

243

Как и у понятия-предшественника ( )

,

где -

кинетические моменты механической системы относительно осей соответственно , .

Ясно, что приёмы вычисления модулей, направляющих косинусов и прочие векторно-преобразовательные процедуры математически идентичны изученным в разделе «статика» и по этой причине здесь опускаются.

При решении конкретных задач чаще дело имеют с поступательным и вращательным движением тел. Это обязывает нас развить рассматриваемый вопрос и в последующих двух подразделах дать конкретные рекомендации по вычислениям кинетических моментов для указанных случаев.

29.2. Правило вычисления кинетического момента поступательно движущегося тела

Н

К правилу вычисления кине-тического момента посту-пательно движущегося тела

а рис.29.2: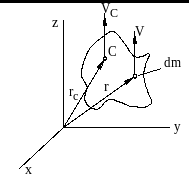 - масса отдельной частицы, - её скорость, - радиус-вектор. - центр тяжести тела, - его скорость, -радиус-вектор, - масса тела.

Напоминаем: - это и сумма дискретных величин, и интеграл, и сумма интегралов.

В связи с этим, из 29.2 получаем:

.

Т.к. для поступательно движущегося тела не зависит от номера частицы, то

29.2

Рисунок 29.2

и приходим к правилу:

к инетический момент поступательно движущегося тела можно вычислять как момент количества движения отдельной материальной точки, масса которой равна массе тела и которая движется вместе с центром его масс.

244

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги