ztm15 (850189)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

нии гантели прижаты к бёдрам и момент инерции системы «человек-гантели-скамья» кг м².

Требуется. – Определить угловую скорость рассматриваемой механической системы во втором её положении.

Решение.- Центр тяжести системы в обоих положениях расположен на оси вращения, реакции подшипников пересекают её. Поэтому и

об/с.

К примеру 29.2

П

29.8

РИМЕР 29.2.- Вывод формулы для вычисления углового ускорения барабана с намотанным на него тросом, к концу которого подвешен груз Дано. – На барабан 1 радиусом намотана невесомая нить, к концу которой подвешен груз 2 массой (см. рис.29.6).

Требуется.- Определить угловое ускорение барабана.

Решение.- Принимаем к рассмотрению систему «барабан-нить-груз». Её кинетический момент имеет две составляющие: .

К

Рисунок 29.6

инетический момент поступательно движущегося груза в соответствии с подразделом 29.2: .

При написании этой формулы целесообразно использовать методы статики - вектор уподобить силе и её модуль умножить на плечо вектора относительно оси - на .

Кинетический момент барабана вычисляем по формуле подраздела 29.3:

.

Итак, .

Теперь вычисляем сумму моментов внешних сил -

(реакции подшипников направлены через ось вращения , поэтому моменты от них равны нулям; единственный ненулевой момент – это момент сил тяжести, приложенных к массе ).

Итак, .

249

П

К примеру 29.3

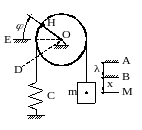РИМЕР 29.3.- Собственные колебания системы «шкив с перекинутым через него невесомым тросом, один конец которого через пружину соединён с неподвижным телом, а ко второму подвешен груз»

Дано. – - радиус шкива; - его момент инерции (относительно оси вращения). - масса подвешенного груза. - жёсткость пружины (см. рис.7).

Т

Рисунок 29.7

ребуется. - Определить период собственных колебаний заданной механической системы.

Решение.- Чтобы иметь меньшее количество математических преобразований, при рассмотрении всех задач на колебания рекомендуем использовать

п равило принятия за начала отсчётов положений статического равновесия механических систем: за начала отсчётов координат (линейных, криволинейных, угловых) при рассмотрении колебательных движений механических систем целесообразно принимать те точки и линии систем отсчёта, с которыми в положении статического равновесия механической системы совпадают её метки.

Поясняем (см. рис. 29.7):

А – горизонталь системы отсчёта, на которой расположен центр тяжести груза при недеформированной пружине;

В – горизонталь системы отсчёта, на которой расположен центр тяжести груза при статическом равновесии рассматриваемой механической системы. Этот уровень и принят за начало отсчёта числовой оси ;

М – текущее (в процессе колебаний) положение центра тяжести груза;

ОD, ОЕ и ОН – положения радиуса-метки на шкиве при, соответственно, недеформированной пружине, в положении статического равновесия и в текущий момент времени.

В положении статического равновесия (это положение, которое занимает механическая система после полного затухания имевших место колебаний) пружина окажется растянутой на некоторую величину ; её называют статической деформацией пружины, определяют по закону Гука - из равенства: ; - это натяжение нити при отсутствии в системе колебаний; из условия равновесия принятой к рассмотрению системы «шкив+охватывающая его нить (без пружины)+груз» следует, что .

В процессе колебаний (в некоторый произвольно взятый момент времени) пружина окажется деформированной на величину . Понятно, что если пренерегать массой пружины и нити (это обычное допущение), то натяжение нити

250

окажется определяемым по формуле (по закону Гука): .

Для решения задачи воспользуемся законом об изменении кинетического момента в форме: .

При этом, из предыдущей задачи видим:

но появляется знак минус (правило прежнее – из статики: если уподобленный силе вектор направлен так, что от одиночного его действия тело будет поворачиваться против хода стрелки часов – плюс; по ходу - минус).

.

Итак, получаем:

Или, с учётом того что , а :

29.9

, где .

Напоминаем, что подобное уже встречалось – см. с.179, 185 и 210. Проверьте себя: «как называется величина »? Выражение для периода колебаний напишите самостоятельно.

П

К примеру 29.4

РИМЕР 29.4.- Определение момента, направленного на опрокидывание орудия набок во время выстрела

Д ано. – Осевой момент инерции снаряда относительно оси (см. рис.29.8) кгм². Время его движения внутри ствола , а угловая скорость на дульном срезе .

Т

Рисунок 29.8

ребуется. - Считая вращение снаряда в стволе равноускоренным, определить момент направленный на опрокидывание орудия набок.

Решение.-

29.12

Нм.

251

29.9. Физический маятник

Схематическое изображение физического маятника

29.9.1. Понятие о физическом маятнике.

Формула для вычисления частоты его колебаний

Ф

13

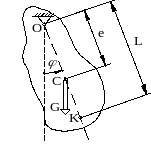изический маятник – это твёрдое тело, совершающее колебательное движение относительно нецентральной горизонтальной оси – см. рис.9, где: - точка подвеса (ось маятника); - центр тяжести, - вес, - момент инерции относительно точки подвеса, - определяющая его положение угловая координата.

З

Рисунок 29.9

аписываем основное уравнение динамики вращательно движущегося тела:

.

Как и для математического маятника, ограничиваемся малыми колебаниями. Получаем:

д ля физического маятника , где .

29.9.2. Об использовании физического маятника для

экспериментального способа определения ускорения свободного падения

29.10

Период его колебаний: .

Для математического же маятника период колебаний определяется формулой 25.11 (с. 180):

29.11

.

Ф изический и математический маятники называют эквивалентными, если они имеют одинаковые периоды колебаний - .

Длину математического маятника, эквивалентного физическому, называют приведённой длиной физического маятника.

После приравнивания правых частей записанных выражений для и , получаем, что

приведённая длина физического маятника определяется по формуле:

, где - масса физического маятника.

252

Точку на физическом маятнике (см. рис.29.9), расположенную на луче на расстоянии от точки подвеса называют центром качаний физического маятника.

С войство взаимности физического маятника:

п

29.13

ериод колебаний физического маятника не изменится, если его центр качаний превратить в точку подвеса; при этом, бывшая точка подвеса превратится в центр качаний нового маятника.

Докажем справедливость результата 29.13 Для этого обозначим: - период колебаний физического маятника, когда точкой его подвеса является ; - период колебаний физического маятника, когда точкой его подвеса является .

Выражаем момент инерции маятника относительно центра качания через приведённую его длину:

.

В написанном алгебраическом преобразовании двоекратно применена математическая связь между моментами инерции относительно параллельных осей (см. подраздел 6.5).

В соответствии с 29.10: .

После подстановки в него выражения для , получаем:

.

Свойство взаимности физического маятника в гравиметрии используют для экспериментально-теоретического определения ускорения свободного падения в различных местах Земного шара и устанавливают, поэтому, различные гравитационные аномалии, что позволяет делать заключения о наличии полостей внутри земной поверхности, оценивать наличие залегающих пород с большими или малыми удельными весами и т.д. В основе метода лежит математическая зависимость, получаемая из последнего выражения:

, где

- экспериментально устанавливаемая величина; её в так называемом оборот-ном маятнике изменяют мельчайшими шажками - пока не добьются равенства и (которое устанавливают с предельно возможным уровнем точности).

253

29.10*. Основные экспериментально-теоретические способы определения моментов инерции тел

Не всегда моменты инерции тел можно установить чисто аналитическим путём. Две основные этому причины: геометрическая сложность форм и неоднородность материала.

К определению момента инерции автомобиля

29.10.1. Нахождение момента инерции тела через превращение его в физический маятник

с экспериментальным определением

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги