ztm21 (850195)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

36.5. Вынужденные колебания линейных систем с одной степенью свободы

В ынужденными колебаниями линейных систем с одной степенью свободы и вязким трением называют движение, описываемое дифференциальным уравнением

36.19

, где

левая часть уравнения взята из 36.11. В правой части:

- возмущающая амплитуда; - возмущающая частота; - возмущающая фаза; - начальная возмущающая фаза.

Если говорить о конкретных примерах, то уравнение 36.19 будет получено для системы, изображённой на рис.2, если вы рядом с силой изобразите и силу . Рекомендуем проделать это самостоятельно.

П

36.20а

о математической классификации 36.19 - это дифференциальное уравне-ние второго порядка, линейное, с постоянными коэффициентами и правой частью (неоднородное, т.е. имеющее функцию времени в явном виде). Поэтому: общее решение уравнения 36.19 можно представлять суммой двух составляющих –

а

, где

- общее решение дифференциального уравнения и

- частное решение неоднородного уравнения.

С

36.20б

оставляющая достаточно подробно рассмотрена в предыдущем подразделе (и малые, и большие сопротивления; изображены графики). Здесь заметим лишь, что по прошествии небольшого промежутка времени после появления возмущающей силы (до минуты - нескольких минут; например, после включения в работу двигателя) составляющая становится пренебрежимо малой по сравнению с . Последняя же, как увидим, во времени сохраняется (поэтому её называют стационарной составляющей вынужденных колебаний); причём она может достигать громадных значений. По этим причинам в вынужденных колебаниях основной интерес представляет .

Если хотят подчеркнуть, что речь идёт о вынужденных колебаниях без учёта затухающей составляющей, то употребляют термин: «чисто вынужденные колебания».

Переходные процессы для механических колебаний имеют относительно небольшую значимость. Поэтому в дальнейшем будут иметься ввиду чисто вынужденные колебания.

345

Частное решение ( ) находим методом неопределённых коэффициентов. При этом, с целью упрощения записей, обозначаем

б

просто .

Т.к. в правой части 36.19 записано , то решение ищем в форме

.

Полученную тройку выражений подставляем в 36.19, причём правую его часть записываем также с учётом обозначения (б). Получаем:

.

Откуда (приравнивая алгебраические выражения при и ) находим

, где

- коэффициент расстройки; - относительный коэф-фициент затухания (безразмерный коэффициент демпфирования);

с учётом 36.20а , т.е.:

, где

-

- уравнение чисто вынужденных колебаний.

является размерной величиной. Для обобщённых же оценок амплитуд вынужденных колебаний более удобны безразмерные величины. Главной из них является коэффициент динамичности ( ). Введём это понятие.

Если частота вынужденных колебаний стремится к нулю (при нагрузки называют статическими), то .

346

К

36.21а

оэффициент динамичности – это отношение амплитуды вынужденных колебаний к амплитуде колебаний той же системы, при тех же действующих силах, с одним лишь отличием – частота возмущающей силы стремится к нулю (если говорить о конечных величинах – то частота возмущающей силы меняется очень медленно, положим за один год на один полный период):

.

Относительный кэффициент затухания различен для различных систем. является непрерывной переменной даже в рамках одной системы (что будет показано в следующем подразделе).

Графики, отображающие уравнения 36.21а и 36.20а, представлены на рис.36.5 и 36.6.

Коэффициент динамичности Сдвиг по фазе

Рис.5 Рис.6

Из них видно:

1. Максимальные значения (при фиксированных , особенно при небольших их значениях) мало отличаются от резонансных ( ) и, поэтому,

в

36.21б

практических расчётах максимальные коэффициенты динамичности можно оценивать резонансными значениями, т.е. вычислять по формуле: .

При малых сопротивлениях (что широко распространено – колебания в воздушной среде, без демпфирующих устройств) они могут принимать очень большие значения. Например, при ;

347

2. Сдвиг по фазе между гармониками, описывающими вынужденные коле-бания и возмущающую силу, может быть различным в интервале от до 180^o:

1. При резонансе равен 90^о;

2. При малых (по отношению к 1,0) сдвиг по фазе близок к 0^о; при больших – близок к 180^о (близок к противофазе).

К примеру о дисбалансных вынужденных колебаниях

ПРИМЕР 36.1. - Дисбалансные вынужден-ные колебания линейной системы с одной степенью свободы

Н

Рисунок 36.7

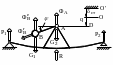а рис.36.7: балка на двух опорах с установленным на нём четырёхполюсным (номинальная угловая скорость ) асинхронным электродвига-телем с короткозамкнутым ротором; - ось вращения ротора; - подвижная горизонталь; мм – величина дисбаланса; - координата, определяю-щая угловое положение ротора; - неподвижная горизонталь, на которой рас-

положен центр вращения при недеформированной балке; - неподвижная горизонталь, на которой расположен центр вращения при неработающем двигателе; - прогиб балки (деформация упругого элемента – пружины) от статической нагрузки (при неработающем двигателе); - текущая деформация балки при работающем двигателе; - модуль суммарной реакции на опорах; Н/м - жёсткость балки; кг - масса ротора; кг - масса статора (неподвижной части электродвигателя и других жёстко связанных с ним деталей). Массой балки пренебречь; - сила инерции от статора; - веса ротора и статора; - модуль переносной силы инерции ротора; - модуль относительной силы инерции ротора; - модуль силы вязкого сопротивления, где Н·с·м^-1.

Для составления дифференциального уравнения рассматриваемого дисбалансного колебания используем метод кинетостатики:

.

348

Проектируем составленное векторное равенство на ось :

, где

;

36.22

;

м/с².

Определяем, по формуле 36.20б, амплитуду вынужденных колебаний, соответствующую работе системы при номинальной угловой скорости ( ) ротора электродвигателя:

мм.

К примеру о дисбалансных вынужденных колебаниях

Видим, что с прочностной точки зрения при номинальном режиме работы амплитуда колебаний незначительна. Но ...

разберёмся с инженерной сутью вопроса.

В

Рисунок 36.8

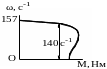зятый к рассмотрению в пример четырёхполюсный асинхронный электро-двигатель с короткозамкнутым ротором чаще всего и применяется для привода различных механизмов. На рис.36.8 представлена обобщённая его механическая характеристика, где жирной линией (от 150 с^-1 до, примерно, 140 с^-1) изображён рабочий её участок. У очень многих рабочих машин нагрузка (М, н·м) является переменно-случайной величиной и, поэтому, возможны режимы работы с различными угловыми скоростями.

349

Асинхронные двигатели применяют не только с 4-мя полюсами, но с 2-мя, 6-ю, 8-ю, иногда и более полюсами. У них левые границы рабочих участков вместо 157 с^-1 равны, соответственно, 235 с^-1, 118 с^-1, 78 с^-1, а правые границы также примерно на 10% меньше левых. У электродвигателей постоянного тока с так называемым параллельным возбуждением рабочие участки механических характеристик подобны рассмотренному на рис.8. У электродвигателей же постоянного тока с последовательным соединением обмоток рабочие участки механических характеристик крутопадающие, т.е. правые границы не на 10% меньше левых, а от в несколько раз до в несколько десятков раз меньше левых. Аналогична картина имеет место и для двигателей внутреннего сгорания. Итак,

п ри рассмотрении вынужденных колебаний анализ всегда надо начинать с предпосылки: частота возмущающей силы ( , или как в рассматриваемом случае, ) - плавающая величина - она может принимать любые значения в определённом интервале (диапазоне).

Но задачи по установлению этих интервалов являются предметом рассмотрения других наук, в частности электропривода.

Заканчиваем рассмотрение примера. Рабочие угловые скорости расположены в диапазоне (140-157) с^-1. Частота собственных колебаний системы ( ) попала в этот диапазон. При из 36.20б получаем:

м мм,

т.е. понятно, что полуметрового размаха ( мм) колебаний рассматри-ваемая механическая система не достигнет - авария произойдёт до этого.

36.6. О необходимости учёта других гармоник при рассмотрении вынужденных колебаний

Возмущающими силами могут быть не только отдельно взятые гармоники (как в рассмотренном примере). Часто инженер имеет дело с разнообразными периодическими функциями времени, отличными от отдельно взятых гармоник.

Два примера периодически изменяющихся во времени сил

Рисунок 36.9

350

На рис.36.9 представлено 2 таких примера: слева – периодическая непрерывная (например в двигателях внутреннего сгорания); справа – периодическая, кусочная, с разрывами 1-го рода. - их периоды.

Из курса высшей математики известна теорема Дирихле, в соответствии с которой всякая периодическая кусочно-непрерывная с разрывами 1-го рода (либо без разрывов) функция может быть представлена рядом Фурье:

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги