ztm3 (850177)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

Закон о трёх силах широко используется при решении задач на равновесие. Покажем переход к нему с помощью ранее описанных методов и опорных фактов.

П

К закону о трёх силах

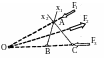усть А (см. рис. 15.14) – произвольная точка на линии действия силы . На линии действия силы возьмём две точки - В и С, такие, чтобы и были непараллельными линии действия силы .

Т

Рисунок 15.14

.к. тело покоится, а силы и пересекают ось , то из получим: .

и не || . Остаётся единственное - сила также пересекает .

Аналогично рассуждая приходим к выводу: сила пересекает и ось .

пересекает и . Значит она, как и , лежит в плоскости АВС.

Но и непараллельны. Пусть О - точка их пересечения.

Рассматриваемая система из трёх сил по условию является уравновешенной. Поэтому для неё . Моменты от сил и относительно точки О равны нулям. Значит нулю равен и момент относительно точки О силы . Но . Остаётся единственное: также проходит через точку О.

Демонстрация приемлемости применяемых методов перехода от заведомо доверительных (не вызывающих сомнений) механических фактов к другим, завершена.

15.4. Рекомендуемая схема подхода к решению задач на определение реакций связей

Первый этап – применяя принцип освобождаемости от связей, в исходной механической системе мысленно выделить и принять к рассмотрению какое-либо тело.

Какое? - Однозначного ответа не существует. Подходящие тела чаще всего «напрашиваются» из постановки задачи. В общем случае вопрос решается методом проб - путём мысленного просмотра различных вариантов – вначале к рассмотрению принимается одно тело, затем второе, третье и т.д., до тех пор, пока не будет найден приемлемый вариант.

65

По результатам мысленно проведенного анализа возможных вариантов, к рассмотрению принимается какое-либо тело и изображается отдельным рисунком.

Изучившие теоретическую механику данной рекомендацией часто не пользуются – представляют этот рисунок мысленно. С целью меньших затрат на качественное усвоение изучаемого материала, студентам от такой «экономии» целесообразно отказываться.

Второй этап – изобразить на рисунке все действующие на тело внешние силы (активные и реакции связей). Чтобы не забыть учесть ту или иную реакцию связи, целесообразно использовать принцип освобождаемости от связей (см. подраздел 13.3).

Изобразите на рисунке необходимые геометрические размеры (расстояния, углы).

Для удобства чтения рисунков тела, активные силы, реакции связей (они обычно неизвестны) и размерные линии изображайте чертёжным инструментом и отличающимися друг от друга линиями. Например, тела изображайте шариковой ручкой синего цвета, активные силы - зелёным цветом, реакции связей – красным. Размерные линии изображайте простым чёрным карандашом.

Третий этап. - Составьте систему уравнений равновесия и решите её.

С целью быстрого воспроизведения в памяти схемы решения задач статики удобно помнить словесную формулу: «тело-силы-уравнения».

1

К условию

примера 15.1

К решению

примера 15.1

5.5. Примеры на определение реакций связей в простейших механических системах

ПРИМЕР 15.1.- На законы о противодействии и о двух силах

Д ано. Механическая система по рис.15.15. ; С – груз, весом .

О

Рисунок 15.15

пределить натяжение нити АВ и усилие в стержне ОВ.

Р

Рисунок 15.16

ешение.- Применяя принцип освобождаемости от связей, принима-ем к рассмотрению и изображаем на рис. 15.16 отдельно груз С, нить ВС и стержень ОВ.

В соответствии с законом о двух силах, для груза С получаем: , причём расположены эти силы на одной прямой, проходящей через точку С.

66

На основании закона о противодействии, записываем: .

Теперь используем закон о двух силах для нити и устанавливаем: .

Вновь применяя закон о противодействии и учитывая предыдущие соотношения, получаем.

a

.

Т.к. силы и сходятся в одной точке, они имеют равнодействующую; мысленно обозначаем её .

Таким образом, стержень ОВ находится в равновесии под действием двух сил - и . На основании закона о двух силах заключаем: сила направлена по стержню ОВ, что и отражено на рис. 15.16.

Теперь для находящегося в равновесии стержня ОВ составляем два уравнения равновесия и решаем их.-

. Откуда , а с учётом а:

кН.

. Откуда

кН.

Замечание.- При написании связи а мы постарались в письменной форме показать все звенья логической цепочки. Это сделано по той причине, что рассматривается 1-й пример на равновесие тел. Но письменное отображение всех звеньев логической цепи требует больших площадей бумаги; кроме того, многократные повторения хорошо понятного вызывает у людей ощущения сходное с оскоминой. По этим причинам, для хорошо понятных из предыдущих изложений логических цепочек обычно на письме показывают лишь начальные и конечные звенья, а промежуточные звенья должны воспроизводиться обучающимися самостоятельно и мысленно. Такой подход наблюдается у авторов всех учебников. Так будем делать и мы. Но не забывать: аксиоматический метод тогда обеспечивает высокую доверительность к получаемым результатам, когда расчётчик может воспроизводить все звенья сооружаемых им логических цепочек.

67

П

К условию

примера 15.2

РИМЕР 15.2.- На закон о трёх силах

Д ано. Механическая система по рис. 15.17. кН, м, м.

Определить реакции опорной поверхности В и в шарнире О.

Р

Рисунок 15.17

ешение.- Применяя принцип освобождаемости от связей, принимаем к рассмотрению тело АОВ (см. рис.15.18). Показываем все внешние, действующие на него силы: - активная сила; - реакция

о

К решению

примера 15.2

порной поверхности; - реакция неподвижного шарнира (направлена через точку С на основании закона о трёх силах).

Составляем для тела АОВ уравнения равновесия и решаем их:

. Откуда:

кН.

Рисунок 15.18

. Откуда:

К условию

примера 15.3

кН.

П РИМЕР 15.3.- На удобство использования приёма разложения сил на составляющие

Д

Рисунок 15.19

ано. У механической системы по рис.15.19 вес подвешенного груза G=10кН; ВО=ОС, , ; стержни АВ, АС и АD невесомы.

Определить усилия в стержнях.

Решение.- Применяя принцип освобождаемости от связей, принимаем к рассмотрению стержень АВ (см. рис.15.20). Показываем все внешние, действующие на него силы:

- сила тяжести (активная сила, передаётся через нить); и - реакции стержней, соответственно, AD и AC. Тройку сил , и представляем, как сходящуюся систему сил, в виде одной – в виде их равнодействующей. Теперь,

68

п

К решению

примера 15.3

рименяя к АВ закон о двух силах, реакцию в шарнире В направляем по стержню.

Составляем уравнения равновесия и решаем их. При этом, с целью облегчения процесса вычислений проекций сил и на оси и , они вначале разложены по осям и .

.

15.25

Рисунок 15.20

.

.

Подставляем в последнее выражение два предыдущих и получаем:

кН.

Теперь находим : кН.

П

К условию примера 15.4

РИМЕР 15.4.- Впервые использован приём отрицательного модуля

Д

15.27

ано. Балка на двух опорах по рис.15.21. кН, м; /м; /м; м, м, м; .

Определить реакции на опорах А и В.

Р

Рисунок 15.21

ешение.- Применяя принцип освобождаемости от связей, принимаем к рассмотрению и изображаем на рис.15.22

балку CABD и все действующие на неё внешние силы.

При этом, модуль равнодействующей от сил, распределённых по закону прямоугольника, кН и проходит она посередине участка АС.

69

М

К решению примера 15.4

одуль же равнодействующей системы сил, распределённых по закону треугольника, определяем как площадь треугольника - кН;

н

Рисунок 15.22

аправлена эта равнодействующая вниз и проходит от точки D на расстоянии, равном одной третьей d.

При изображении реакций

и используем приём отрицательного модуля: безошибочно указать положительные направления (особенно для Y_A и Y_B) пока сложно и, поэтому, вначале эти направления указываются наугад; если в результате последующих вычислений модуль силы окажется отрицательной величиной, это будет означать, что действительное направление реакции противоположно принятому.

С

Приём нахождения неизвестного плеча

оставляем уравнения равновесия и решаем их. При этом, для вычисления момента силы относительно точки А можно использовать

15.26

приём нахождения неизвестного плеча (см. рис.15.23) -

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги