ztm16 (850190)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

П

ба

олученное выражение объединяем с последним равенством из строки (а) и получаем: , а с учётом допущения 29.20 -

.

С другой стороны . Таким образом:

в

.

Учитываем, что , а , где - алгебраическая величина - если расположена выше точки (см. рис.18), то больше нуля, если ниже – меньше нуля). Тогда (в) принимает вид:

.

Итак,

29.21

геометрическая ось гироскопа описывает коническую поверхность вокруг вертикали с угловой скоростью

,

из которой видно:

29.22

чем меньшим будет непопадание центра тяжести гироскопа в центр сферического движения и большим модуль угловой скорости собственного вращения ( ), тем меньшей будет угловая скорость прецессии его оси.

ПРИМЕР 29.8.- Вычисление угловой скорости прецессии гироскопа

Дано. – Момент инерции гироскопа кг^..см², масса кг, непопадание центра масс в центр сферического движения мкм. Модуль угловой скорости собственного вращения гироскопа об/мин.

Требуется. - Вычислить модуль угловой скорости прецессии гироскопа. Решение.- угловых градуса за сутки.

265

29.15*. О гироскопе с двумя степенями свободы, гироскопическом моменте и гироскопических реакциях

П

Рисунок 29.20

Принципиальная схема гироскопа

с двумя степенями свободы

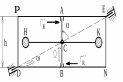ринципиальная схема гироскопа с двумя степенями свободы изображена на рис.29.20: - гироскоп, - его рама. можно представлять в виде маховика-тороида, - его ось вращения; и - подшипники, - центр тяжести гироскопа. Гироскоп относительно рамы вращается с угловой скоростью . В свою очередь, рама принудительно вращается вокруг оси с угловой скоростью ( и - подшипники, в которых расположены цапфы рамы).

Приведенная принципиальная схема гироскопа с двумя степенями свободы является моделью реальных устройств. Например, ротор электродвигателя троллейбуса – это гироскоп, а поворачивающийся на поворотах его корпус – рама гироскопа. Колёсная пара и рама автомобиля – это также гироскоп с двумя степенями свободы. И т.д.

Замечено: если угловая скорость рамы не равна нулю ( ), то гироскоп оказывает сопротивление повороту его оси относительно инерциальной системы отсчёта. И явление это, вновь-таки, не есть что-то необъяснимое – оно также надёжно предсказывается методами теоретической механики. Для показа этого обратимся к рассмотренной в предыдущем разделе формуле (б):

.

Здесь (начало центромассовой системы координат) написано вместо на основании изложенного в подразделе 29.11.

Т.к. , то ясно, что

29.23

величина имеет размерность момента силы; её называют «гироскопическим моментом»; он приложен к раме со стороны гироскопа.

Гироскопический момент является инженерно ощутимой величиной. Например, при , кг^..м², и он равен кН^.м ( Н^.м).

266

Направлен гироскопический момент перпендикулярно и , и ; следовательно направлен перпендикулярно плоскости рамы (что следует из правил векторного произведения).

В условиях схемы, изображённой на рис.29.20, гироскопический момент уравновешивается парой сил , приложенных к оси гироскопа со стороны рамы (со стороны подшипников и ). Эти силы называют «гироскопическими реакциями».

Из рассмотренных равенств видно, что

29.23

гироскопические реакции – это силы, приложенные к оси гироскопа со стороны рамы, расположены в её плоскости и направлены так, что если мысленно приложить их к вектору большой угловой скорости, то он завращается в том направлении, чтобы из двух возможных вариантов (векторы сонаправлены - векторы противоположно направлены) раньше появилась сонаправленность большой и малой угловых скоростей. Модуль каждой из гироскопических реакций определяется формулой:

, где

- угол между векторами и ;

- расстояние между подшипниками гироскопа.

Р

30.1а

ассмотренное явление используют не только для определения гироскопических реакций (с целью их учёта в прочностных и других инженерных расчётах), но, в сочетании с приборами-указателями направлений, используют для решения задач по стабилизации движений. В частности, гироскопические силы используют для обеспечения также точности в направленности орудия движущегося танка на цель; для предотвращения морской качки; для обеспечения вертикального положения двухколёсных автомобилей и вагонов на однорельсовых дорогах; и т.д.

30.2

267

30. Закон об изменении кинетической энергии

Для формулировки закона, а затем его использования, необходимо ввести ряд новых понятий. Им отводятся подразделы 30.1-6.

3

К понятиям о работе и мощности силы

0.1. Понятия о работе и мощности. Общие формулы для их вычисления

В качестве мер механических действия, кроме силы, её момента и импульса, пользуются также понятиями «работа» и «мощность» силы.

Пусть (см. рис.30.1) - траектория материаль-ной точки , - действующая на неё сила (в общем случае переменная – и по модулю, и по направлению). И пусть промежуток времени, за который материальная точка переместилась из положения «1» в положение «2», является беско-нечно малой величиной, т.е. пусть .

Т

Рисунок 30.1

огда вектор перемещения точки также будет бесконечно малой величиной - .

По определению,

30.1

величину называют элементарной работой силы .

Если движение задано естественным способом, то, как уже рассматривалось в кинематике, с точностью до бесконечно малых второго порядка малости и, поэтому, , где - орт подвижной касательной оси. Тогда:

,

где - проекция силы на подвижную касательную ось.

Если же движение задано координатным способом, то

и, учитывая правила скалярного произведения (произведения ортогональных векторов равны нулям), получаем

30.1б

.

В еличину называют работой силы на конечном перемещении точки её приложения (из положения «1» в «2»).

268

Е

30.6а

сли точка приложения силы имеет скорость , то величину называют мгновенной мощностью силы . Слово «мгновенной» обычно опускают.

30.6б

, т.е.:

м

30.3

гновенная мощность силы - это величина, определяемая математическими выражениями .

Наряду с понятием «мгновенная мощность силы» широко оперируют понятием «средняя мощность силы». Что это за понятие?

Пусть - это работа силы за промежуток времени . Тогда:

в

30.4

еличину, определяемую из выражения ,

называют средней мощностью силы .

У

К понятию

«средняя мощность силы»

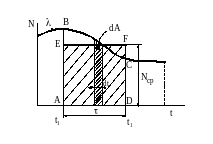добно среднюю мощность силы представлять геометрически. С этой целью приводим рис.30.2, где: линия в системе координат отображает изменение мгновенной мощности во времени. В соответствии с введенными понятиями площадь прямоугольника равновелика площади фигуры .

Д

Рисунок 30.2

о сих пор речь велась об отдельной силе. Но понятия «работа» и «мощность» распространяется и на системы сил.

П

30.7

усть на некоторую принятую к рассмотрению механическую систему дей-ствует сил ( ). По определению:

30.5

- элементарная работа системы сил, действующей на принятую к рассмотрению механическую систему;

269

- мгновенная мощность, развиваемая системой сил, действующих на принятую к рассмотрению механическую систему.

- средняя мощность, развиваемая системой сил, действующих на принятую к рассмотрению механическую систему.

Из введенных понятий с очевидностью следует, что суммарная элементарная работа и суммарная мощность связаны между собою той же зависимостью 30.3, которой связаны элементарная работа и мощность отдельно взятой силы.

3

К выводу формулы для вычисления работы силы тяжести

0.2. Примеры вычисления работ сил для часто встречающихся случаев

30.2.1. Работа силы тяжести на

к онечном перемещении точки её приложения

П

8

усть материальная точка перемещается из положения в положение по произволь-ной траектории - см. рис.3.

.

Рисунок 30.3

9

.

Принято называть: - геодезическая высота начального положения точки; - геодезическая высота конечного положения точки; - разность геодезических высот. Таким образом:

- работа, совершаемая силой тяжести, не зависит от формы траектории точки её приложения и равна произведению модуля силы тяжести на разность геодезических высот начального и конечного положений этой точки.

30.2.2. Работа упругой силы на конечном перемещении точки её приложения

На рис.30.4: - тело, к которому приложена упругая сила ; - положение тела, соответствующее недеформированному состоянию пружины;

270

- координ

К выводу формулы для вычис-ления работы упругой силы

ата, определяющая некоторое текущее положение тела .

В

30.10

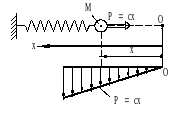соответствии с законом Гука , где - жёсткость пружины, - величина её деформации. Изображённый на рис.30.4 треугольник называют эпюрой упругой силы.

Работу упругой силы при перемещении тела из некоторого деформированного состояния, определяемого координатой , в недеформи-рованное ( ), называют полной работой упругой силы.

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги