ztm2 (850176)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

13. Блок других, наиболее используемых в статике, понятий и опорных фактов

1

Исходная механическая система

3.1. Понятия об исходных механических системах и телах, внешних и внутренних силах, связях и их реакциях

И

Рисунок 13.1

сходная – это та механическая система, с которой начинают её анализ (см. рис.13.1 и 13.3). Абсолютно твёрдое тело (кратко: тело) – это принятая к рассмотрению та или иная совокупность неподвижных друг относительно друга частиц механической системы.

Т

К понятию «тело»

Рисунок 13.2

ело – понятие относительное. Им может быть отдельная деталь (гайка, болт, шестерёнка, доска и т.п.), часть детали, совокупность деталей, несколько целых деталей в совокупности с частями других деталей. Например, для представ-ленной на рис.13.1 конструкции при определении неизвестной силы (при известной ) за тело может быть принята вся совокупность деталей 1-2-3-4-5-6-7.

Если же необходимо определить величину затяжки болта, то за тело может быть принята совокупность конструктивных элементов, представленная на рис.2 (в которую входят полоса 2, шайба 4 и верхняя часть болта 3).

В соответствии с введенным понятием, за абсолютно твёрдые тела могут приниматься не только твёрдые, но и деформируемые физические тела – заведомо натянутые трос, цепь, растянутая или сжатая пружина, газ или жидкость, расположенные в цилиндре с поршнем; и т.д.

А если заведомо неизвестно подвижны или неподвижны одни совокупности частиц относительно других? - Рассмотрение такого типа задач также является предметом теоретической механики, но третьей её части – динамики.

Действующие на тела силы принято делить на внешние и внутренние. Внутренние – это силы, действующие между частицами, принадлежащими принятому к рассмотрению телу. Внешние силы – это силы, приложенные к телу со стороны частиц, не принадлежащих рассматриваемому телу.

Понятия внешних и внутренних сил также относительные. Так, если для тела по рис.13.2 силы - внешние, то для тела по рис.1 эти же силы являются внутренними.

39

По отношению к принятому к рассмотрению телу, другие части исходной механической системы называют связями.

Силы, действующие на принятое к рассмотрению тело со стороны связей, называют реакциями. В отличие от них остальные внешние силы активные.

Поясняем.- Для тела, изображённого на рис.2, механическая система по рис.13.1 является исходной и, поэтому, для него связями являются: полоса 1 и не изображённая (на рис.13.2) часть тела болта (с гайкой и шплинтом). Соответственно реакциями являются силы и ; - это сила, приложенная к рассматриваемой части болта со стороны отброшенной его части. - сила, приложенная к полосе 2 со стороны полосы 1;

Захват подъёмного устройства

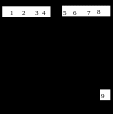- нормальная её составляющая, - касательная (расположенная в плоскости соприкосновения полос – обусловлена силами сцепления, о чём подробнее речь будет вестись в подразделе 15.8).

Понятия связей и их реакций поясняем ещё на одном примере.

Если из исходной механической системы, изображённой на рис.13.3, к рассмотрению принята планка-стяжка 1, то для неё связями будут цилиндрические выступы рычагов 2 и 7 (но нельзя для рассматриваемого случая связями считать стержни 3 и 6, а также серьгу 5 и крюк 4).

Е

Рисунок 13.3

сли же из исходной механической системы по рис.3 к рассмотрению принят рычаг 2, то для него связями будут стер-жень 3, планка 1 и поднимаемый груз 9.

13.2. Аксиома о противодействии. О главных векторе и моменте внутренних сил

Пусть любая одна частица взаимодействует с любой другой частицей. Силу , с которой частица 1 действует на частицу 2, назовём действием. Тогда реакцию 2-й частицы на 1-ю (силу ) называют противодействием.

А

13.1

ксиома о противодействии: действие и противодействие образуют систему противоположных сил, т.е.: = и расположены они на одной прямой.

40

Силы действия и противодействия могут быть контактными (от непосредственного соприкосновения тел) и дальнедействия (передаваемые через поля – гравитационные, магнитные, электрические, электромагнитные и др.).

Иногда говорят: «Аксиома – положение, принимаемое без доказательств».

На примере аксиомы противодействия покажем, что подобные высказывания нельзя считать удачными.

1654-й год. Магдебург. Бургомистр Отто фон Герике демонстрирует свойство вакуума – опыт, обошедший печать всех развитых стран мира: два медных полых полушара соединены между собой по экваториально-кольцевой поверхности; из внутренней полости образовавшейся сферической оболочки выкачан воздух (через краник); оболочки-полусферы растягивают (и не могут разъединить) две восьмёрки лошадей (т.е не 8 против одной, или двух, или четырёх, а 8 против 8-ми).

Ещё и сегодня мы наблюдаем народные состязания по перетягиванию каната. И в этом случае всем, из непосредственных наблюдений, ясна необходимость равенства числа соперников по обоим концам каната.

Справедливость закона-аксиомы противодействия можно наблюдать также на примере одинаковости деформаций буферных пружин двух взаимодействующих вагонов (как при их сцепке, так и при движении поезда).

Законом о противодействии Человечество пользуется не менее 3-х веков. Во всяком случае, уже в «Математических началах натуральной философии» (И.Ньютон, 1687 год) мы находим: «Действию всегда есть равное и противоположное противодействие, иначе: взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. Если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется. Если кто нажимает пальцем на камень (здесь Ньютон повторяет рассуждения Г.Галилея), то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно … она с равным усилием оттягивается к камню … Относительно притяжений дело может быть изложено вкратце следующим образом … Я производил опыты с магнитом и железом: если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии».

Внутренние силы любой принятой к рассмотрению механической системы состоят из совокупности противоположных сил, но для любой двойки таких сил равны нулю и главный вектор, и главный момент. А сколько бы нулей не складывалось результатом также будет нуль. Таким образом:

д

13.2

ля внутренних сил любой механической системы равны нулю и главный вектор, и главный момент, т.е. при вычислениях главных векторов и моментов внутренние силы можно не учитывать.

41

13.3. Аксиома о равновесии, принцип освобождаемости от связей, сопутствующие понятия

Описанные в подразделе 13.1 тела называют несвободными. В подавляющем большинстве случаев с ними и приходится иметь дело в статике, но укоренившийся термин «равновесие» обязывает нас ввести и понятие свободного тела. Это нужно сделать ещё и потому, что статика является лишь частью единой теоретической механики, а объектами рассмотрения кинематики и динамики чаще всего являются свободные тела.

Свободное тело – это тело, перемещение которого другими телами не ограничено. Если использовать приём образности мышления, то свободное тело мысленно можно представлять в виде воздушного шара, птицы в полёте, вертолёта, подводной лодки и т.п.

Понятие «равновесие свободного тела» (кратко: «равновесие тела») в полном своём объёме требует знаний кинематики, но в инженерной практике чаще предстаёт в форме покоя тела. Поэтому, при изучении статики можно считать, что «равновесие тела» - это его покой.

В динамике понятие «равновесие тела» будет расширено (будет: «тело считается находящимся в равновесии, если оно покоится, или движется относительно инерциальной системы отсчёта поступательно, прямолинейно и равномерно»; при этом, за инерциальную систему отсчёта в подавляющем большинстве конкретно встречающихся случаев достаточно принимать систему координат, связанную с Землёй - Геоцентрическую).

Специалисты по истории теоретической механики сообщают, что термин «равновесие», вместо древнегреческого «равномоментность», ввёл Симон Стевин (Бельгия, годы жизни: 1548-1620); первым он начал использовать и правило параллелограмма сил. Этим фрагментом исторического экскурса мы иллюстрируем приводившееся во введении утверждение о международном и многовековом процессе совершенствования излагаемого курса.

А

13.3

ксиома о равновесии: если главные вектор и момент всех приложенных к телу сил равны нулю, то такое тело находится в равновесии. Справедливо и обратное утверждение – если тело находится в равновесии, то главные вектор и момент всех действующих на него сил равны нулю. Уместно вспомнить:

1) результат 12.18 - равенство нулю главного момента не зависит от выбора центра, относительно которого он вычисляется;

2) результат 13.2 - при рассмотрении аксиомы о равновесии достаточно учитывать лишь внешние силы.

Называют:

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги