ztm2 (850176), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

П

Преобразование к равнодействующему винту

ереходим к рассмотрению последнего, шестого возможного случая - случая « не и не ».

С

Рисунок 14.1

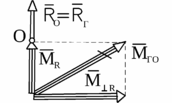целью упрощения исходной системы сил на первом этапе преобразования принимаем систему, состоящую из силы , приложенной в точке О (относительно которой вычислялся главный момент исходной системы) и двух пар сил с моментами , , удовлетворяющих условию: = (см. рис.14.1).

На втором этапе преобразования силу и пару сил с моментом заменяем одной силой , равной (так, как это делалось в подразделе 12).

Таким образом:

47

с

14.5

истема сил с ненулевыми главными вектором и моментом, у которой главный момент и не перпендикулярен, и не параллелен главному вектору, приводится к равнодействующему винту, ось которого не проходит через центр О, относительно которого вычислялся главный момент. Сила этого винта ( ) равна главному вектору исходной системы, а момент ( ) равен той ортогональной составляющей главного момента, которая параллельна главному вектору.

Переходим к определению положения точки А, через которую проходит ось равнодействующего винта.

14.5*. Формулы для определения положений точек пересечения равнодействующей (или оси равнодействующего винта) с координатными плоскостями

Точки пересечения оси равнодействующего винта (или прямой расположе-ния равнодействующей) с координатными плоскостями условимся называть «метками». Их координаты (вначале приведём результат, затем обоснуем его) -

на плоскости :

14.6а

, ;

на плоскости :

14.6б

, ;

на плоскости :

14.6 в

, ,

где

- проекции главных вектора и момента на оси ;

- направляющие углы для главного вектора ;

- проекция главного момента на ось, сонаправленную с главным вектором.

Формулы 14.6а получены следующим образом.-

Зависимость 12.17 позволяет записать тождество:

48

а

Воспользовавшись способом перестановки индексов (см. подраздел 12.11) и учитывая, что , в левой части a получаем:

b

.

Главные моменты представляем тремя составляющими:

с

;

d

.

Подставляем b, c, d в тождество a и получаем формулу 14.6а – путём приравнивания коэффициентов при ортах и .

Замечание: выражение

( ),

получаемое от приравнивания коэффициентов при орте , можно использовать для проверки правильности проведенных вычислений.

Аналогично получаются формулы 14.6б и 14.6в.

14.6. Закон о моменте равнодействующей

Пусть исходная система сил приводится к равнодействующей ( ).

В соответствии с проведенным в подразделах 1 – 4 анализом, это может иметь место лишь в случае: .

Б

14.8

ерём произвольный центр В, не расположенный на линии действия и обозначаем:

- это главный момент относительно центра В исходной системы ( - число её сил, а - момент относительно центра В -той составляющей этой системы);

14.9

- главный момент относительно центра В равнодейст-вующей (т.к. сила одна, то главный момент равен моменту этой силы).

Исходная система сил и её равнодействующая – это эквивалентные системы и, поэтому

49

,

т.е. получаем:

) = -

е

14.7

сли система сил имеет равнодействующую ( ), то её момент относительно произвольного центра В равен сумме моментов (относительно того же центра) всех, входящих в эту систему, сил.

Опорный факт 14.7 часто называют «законом Вариньона» (Пьер Вариньон, Франция, годы жизни: 1654-1722).

14.7. Основные разновидности систем сил

произвольная пространственная;

пространственная сходящаяся (линии действия всех сил пересекаются в одной точке);

пространственная параллельная (в ней могут быть как сонаправленные, так и противоположно направленные силы);

произвольная плоская система сил;

плоская сходящаяся;

плоская параллельная система сил.

Ответьте на вопросы: к какому простейшему виду можно привести сходящуюся систему сил, систему параллельных сил?

14.8. Начальные сведения и отдельные результаты к вопросу о приведении к простейшему виду распределённых систем сил

Если сила распределена по поверхности, то пользуются понятием «удельное давление» ( ) - это частное от деления элементарной силы на бесконечно малую площадку , к которой эта элементарная сила приложена, т.е.

.

Единицы измерения удельного давления: Н/м² =Па = Паскаль; кГс/м²=атмосфера.

Если удельное давление известно, то, в соответствии с введенными понятиями, главный вектор непрерывно распределённой системы сил определяется формулой:

.

50

Э

b

лементы распределённо-параллельных систем сил обычно сонаправлены и действуют нормально к площадкам своего приложения. Рассмотрением этого случая и ограничиваемся.

Если, при этом, , то

,

г

14.10

де - площадь поверхности, на которую действует рассматриваемая система распределённо-параллельных сил.

Для протяжённых тел (когда один размер площади приложения распределённо-параллельной систем сил намного больше второго) эту систему сил считают распределённой по линии и пользуются понятием «интенсивность нагрузки» (которую будем обозначать буквой ). Единицы измерения интенсивности нагрузки: Н/м; кГс/м и т.д.

В

Наиболее часто встречающиеся эпюры параллельно-распределённых нагрузок

14.11

стречаются различные законы распределения сил. Но этот вопрос не является предметом изучения теоретической механики и, поэтому, ограничиваемся рассмотрением наиболее часто встречающихся случаев, представленных на рис.5:

а ) прямоугольный закон, распределения нагрузки; б) треугольный;

в) трапецеидальный;

г

14.12

) параболический.

Для перечисленных 4-х случаев задаёмся целью определить модули равно-действующих и положе-ния линий их действия. Пусть А – точки пересече-ния равнодействующих с осями , а .

В соответствии с введенными понятиями

Рисунок 14.2

а

с

.

Координату определим воспользовавшись законом о моменте равнодействующей:

.

51

Откуда:

.

Беря интегралы a и b получаем:

п ри прямоугольном законе отображения параллельно-распределённой нагрузки равнодействующая делит отрезок , к которому нагрузка приложена, пополам, а модуль равнодействующей определяется путём вычисления площади этого прямоугольника (произведение интенсивности на );

п ри треугольном законе отображения параллельно-распределённой нагрузки равнодействующая проходит через центр тяжести треугольника т.е. , а её модуль равен площади того же, изображающего нагрузку, треугольника (равен половине произведения на );

п ри параболическом законе отображения параллельно-распреде-лённой нагрузки равнодействующая проходит на расстоянии от вершины параболы, а её модуль равен двум третям площади прямоугольника со сторонами и (в который на рис.5а вписана эпюра, изображающая параболическую нагрузку).

При сложных законах отображения параллельно-распределённых сил для определения модуля равнодействующей и расположения линии её действия удобно применять приём разбиения сложной фигуры на простые. Иллюстрируем этот приём на примере трапецеидальной эпюры нагрузки.

Трапецию ОВСЕ (см. рис.5в) разделяем на прямоугольник ОВDЕ (эту фигуру считаем первой) и треугольник ВСD (фигура 2).

Для модуля равнодействующих получаем:

д ля прямоугольной части нагрузки - ;

для треугольной - ;

для трапеции - .

Теперь определяем положение линии действия равнодействующей .

52

В соответствии с законом Вариньона

.

Из 14.10 и 14.11:

.

Из последних трёх равенств и выражений а получаем:

.

14.13

14.9. О центрах тяжести

С пренебрежимо малой погрешностью для подавляющего большинства решаемых задач можно считать, что сила тяжести – это равнодействующая параллельно-распределённой системы сил, приложенных к частицам тела со стороны поля земного тяготения.

Вес тела – это модуль силы тяжести.

Удельный вес – это вес единицы объёма тела.

Центр тяжести тела – это такая его точка, через которую проходит сила тяжести, независимо от положения тела, относительно Земли.

Понятие о центре тяжести тела ввёл Архимед (287-212 до н.э.) – в трактате «О весах» он писал: «Центр тяжести тела – это точка пересечения отвесных линий при подвесе этого тела за различные точки».

Для определения положений центров тяжести тел используют экспериментальные и теоретические способы.

Из экспериментальных наиболее распространены способы подвешивания и взвешивания тел.

С

14.14

пособ подвешивания: тело два раза подвешивают на нити (цепи, тросе, верёвке и т.п.) и находят точку пересечения двух экспериментально установленных направлений. С точки зрения получения минимальной погрешности, угол между определяемыми направлениями надо принимать близким к 90^о.

С

14.15

пособ взвешивания целесообразно использовать для тел протяжённой формы. Рекомендуем студентам «открыть» (разработать и описать) его самостоятельно (после изучения раздела «Равновесие тел»).

Экспериментальные способы удобно использовать в случае тел сложной конфигурации и составленных из деталей, имеющих разные удельные веса материалов, из которых они изготовлены.

Однако, несмотря на простоту, экспериментальные способы не всегда применимы. Например, при отсутствии конструкции (что имеет место на стадии проектирования устройств и сооружений), при больших размерах тел, при отсутствии возможности прикрепить к телу гибкую связь.

53

П

Способ разбиения тела на части

ри теоретическом определении положений центров тяжести тел сложной конфигурации используют приём разбиения исходного тела на части -

Характеристики

Список файлов книги