ztm13 (850187)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

в частности, с книги «Батуев С.Г. и др. Инженерные методы исследования ударных процессов.- М.: Машиностроение, 1969.- 248с.». Но и рассмотренный пример, в котором ударная сила оказалась в 5000 раз большей веса шарика, убедительно поясняет будущему инженеру почему неотъемлемой составляющей оборудования машиностроительных заводов являются различного типа молоты и ковочные машины, объясняет причину присутствия практически в каждом доме обыкновенного молотка. Но ... продолжим иллюстрацию применимости закона об изменении количества движения рассмотрением ещё одного примера, также на ударное явление, но в ином аспекте.

Рассмотрение примера предваряем понятием:

е

27.9

сли шарик, двигаясь по нормали к неподвижной поверхности, ударяется о неё со скоростью , а отскакивает с , то отношение называют коэффициентом восстановления скорости;

экспериментальные данные показывают, что при скоростях удара до 10 м/с коэффициенты восстановления скорости имеют следующие примерные значения:

с

Скорости шариков до

и после соударения

текло о стекло - 0,93; слоновая кость о слоновую кость - 0,88; сталь о сталь - 0,55; дерево о дерево - 0,5. Ясно, что если удар наносится по подвижному телу, то в числителе и знаменателе формулы 27.9 будут фигурировать разности между скоростями до и после удара.

ПРИМЕР 27.5.- Прямой центральный удар двух шаров

Д

Рисунок 27.2

ано. – По одной прямой перемещается два шарика с одинаково направленными скоростями и . 1-й шарик догоняет второй ( м/с). Массы шариков: г; г. После удара скорости шариков изменяются – становятся равными и (ясно, что модуль скорости становится меньшим модуля скорости ).

Требуется. - Считая известным коэффициент восстановления скоростей

а

,

определить модули и скоростей шариков после их соударения.

Решение.- Принимаем к рассмотрению систему, состоящую из обоих шариков.

Для неё

217

б

где - количество движения системы из 2-х шариков после удара и до него; - импульсы сил тяжести и нормальных реакций. Замечание: ударные силы являются внутренними и, поэтому, в уравнении не учитываются.

Спроектировав векторное равенство (б) на направление скоростей, получаем:

в

.

Для определения неизвестных и решаем систему алгебраических уравнений (а) и (в):

Чтобы избавится от неизвестной первое уравнение умножаем на (- ), второе на “1” , полученные уравнения складываем и т.д. ... после алгебраических преобразований получаем:

. .

После подстановки заданных численных значений определяем: м/с; м/с .

2

К постановке вопроса о равновесии оболочки

с текучей средой

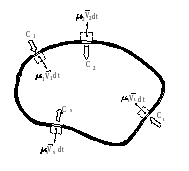
7.6. Условие равновесия оболочки с ответвлениями и установившимся в ней движением текучей среды

Н а рис.27.3 изображена механическая система, оконтуривающую оболочку которой в нескольких местах пронизывают потоки текучей среды (обычно жидкость). По одним частицы втекают внутрь оболочки, по другим вытекают. Потоки характеризуют

с екундные массы

а

т

Рисунок 27..3

.е. это протекающие через поперечные сечения потоков за единицу времени массы

текучей среды;

218

1, 2, ... , i, ... , N - номера потоков текучей среды; - средние по поперечным их сечениям скорости частиц.

Пусть оболочка имеет неизменяемую форму и неподвижна относительно инерциальной системы отсчёта, а - действующий на неё главный вектор внешних сил.

Принимаем к рассмотрению совокупность частиц, которая в момент времени расположена внутри оболочки. Количество её движения - .

Локальная аксиома (о постоянстве содержащегося в оболочке количества движения):

П

27.10

ри установившемся движении текучей среды, протекающей через оболочку с ответвлениями, содержащееся в ней количество движения является постоянной во времени величиной.

У

27.11

становившимся называется такое движение текучей среды, при котором .

П

К выводу условия равновесия оболочки

с текучей средой

ринятая к рассмотрению для момента времени механическая система к моменту изменит свою форму – на рис.4 эти изменения отображены 4-мя прямоугольниками (но мысленно представляется не 4, а прямоугольников - -ый; кроме того, в направлении скоростей размеры таких прямо-угольников – бесконечно малые величины - определяемые произведениями ).

Р

Рисунок 27.4

ис.4 помогает увидеть, что в момент времени количество движения принятой к рассмотрению механической системы определяется выражением:

.

Откуда:

.

Учитывая 27.5, т.е. учитывая, что , из последнего выражения получаем:

219

.

Векторы , которые параллельны соответствующим векторам скоростей , направлены внутрь оболочки и модули которых вычисляются по формулам , называем направленными внутрь оболочки секундными количествами движения потоков текучей среды. Тогда последнее выражение принимает вид:

.

Итак, получено

у словие равновесия оболочки с ответвлениями при уста-

новившемся режиме движения протекающей в ней текучей среды:

- для оболочки с ответвлениями при установившемся движении в ней текучей среды главный вектор всех внешних сил и секундных количеств движения, направленных внутрь объёма, равны нулю.

Замечание.- Определение направления движения потоков не является предметом теоретической механики. Это рассматривается в гидравлике. Но подчёркиваем: секундные количества движения следует направлять внутрь оболочки, независимо от того втекающим или вытекающим является поток.

Результат 27.11 применительно к оболочке с одним входом и одним выходом известен как хорошо проверенное жизнью уравнение Эйлера об изменении секундного количества движения жидкости.

К силе действия струи брандспойта

ПРИМЕР 27.6.- Сила действия струи брандспойта

Д ано. – Из брандспойта (см. рис.27.5) вытекает струя воды со скоростью м/с. Диаметр наконечника мм. К стене струя расположена перпендикулярно и о неё разбивается.

Требуется. - Определить давление струи на стенку.

Р

Рисунок 27.5

ешение.- Принимаем к рассмотрению часть струи, расположенную между плоскостью стены, круговым сечением

220

(диаметром мм) и цилиндрической поверхностью диаметра (безразлично какого диаметра, но такого, чтобы скорости частиц воды, пересекали эту цилиндрическу поверхность перпендикулярно).

Определим внешнюю силу , действующую на принятую к рассмотрению часть струи со стороны поверхности стенки.

Записываем условие равновесия 27.11 применительно к рассматриваемому случаю:

=0, где

- сила тяжести принятой к рассмотрению части струи - направлена вниз;

- секундное количество движения втекающей через сечение жидкости (направлено внутрь рассматриваемого объёма);

- секундное количество движения вытекающей элементарной струйки (с номером ), она по нормали пересекает цилиндрическую поверхность диаметра ; - это символ суммы секундных количеств движения всех элементарных струек, расположенных веером в плоскости стены.

Проектируем составленное векторное уравнение на направление . Получаем:

.

Через входное круглое сечение (диаметром м) за 1 секунду протечёт столбец воды длиной . Масса этого столбца:

, где

кг/м³ - плотность воды.

Тогда секундное количество движения

Итак, давление, производимое на стену рассматриваемой струёй воды равно и направлено слева-направо.

Замечание: если бы скорость струи была не м/с (как в рассмотренном приме-ре), а положим м/с, то давление равнялось бы ! В эксперимен-тах достигаются скорости струй до м/с и более. Большой разрушительной силе струй нашли применение в технике - гидроотбойка угля (существуют так называемые гидрошахты); струями воды режут бумагу, дерево, стекло и пр.

221

27.7. Начальные сведения о ракетодинамике

27.7.1. Введение в подраздел

Вторая половина 20-века ознаменовалась широким вхождением в человеческую практику ракетной техники - и для военных целей, и для исследований космоса. Инженерные достижения в этой области огромны. Пока они, в большинстве своём, относятся к закрытой тематике. Но есть в этих вопросах и много хорошо известного, причём основополагающего. Инженер обязан это знать, ибо путь решения возникающих в практической его деятельности задач может пройти именно через знание основополагающих методов ракетодинамики.

Кроме того, инженер обязан обладать высокой технической культурой, умеющим на основе точного знания отвечать на многие интересующие людей вопросы. Один из них: «Нога человека уже ступила на Луну. Но может ли землянин побывать на планетах Солнечной системы (и непосредственно увидеть что там происходит)? Сможет ли побывать на планетах за пределами Солнечной системы»?

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги