ztm13 (850187), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

Ответить на такие волнующие Человечество вопросы позволяют уравнение Мещерского и вытекающие из него формулы Циолковского.

27.7.2. Уравнение Мещерского

(основное уравнение динамики тела переменной массы)

Н

К выводу уравнения Мещерского

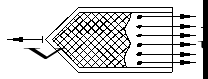а рис.6 изображена оболочка, внутри которой размещено вещество, частицы которого могут из неё извергаться (в результате, например, горения).

Такое устройство называют ракетой.

Задаёмся целью составить уравнение её движения.

Для этого рассматриваем 2 момента времени - и .

П

Рисуно 27.6

усть в момент времени скорость ракеты относительно инерциальной системы отсчёта - , а её масса (рассматриваемая как переменная величина) - .

Тогда, в соответствии с принятыми обозначениями, её количество движения: .

По причине извержения частиц (со скоростью относительно ракеты) к моменту времени абсолютная скорость этой ракеты возрастёт - на беско-

222

нечно малую величину и станет равной , а масса уменьшится, и также на бесконечно малую величину - на . Изменится, поэтому, к моменту времени и количество движения рассматривавшейся в момент времени механической системы; оно станет равным:

,

где - абсолютная скорость отделяющихся частиц (их скорость относительно инерциальной системы). На основании закона сложения скоростей: ( - переносная скорость). Поэтому получаем:

(член опущен как бесконечно малая величина второго порядка малости).

Разделив левую и правую части последнего математического выражения на , получаем:

, где - это ускорение ракеты,

а - знакомая из подраздела 22.6 секундная масса извергающихся из ракеты частиц.

В том же подразделе 22.6 вводилось понятие «секундное количество движения текучей среды». Здесь им является вектор , но, в отличие от предыдущего случая, - относительное, а не абсолютное, секундное количество движения (вычисляемое по скорости извергаемых частиц относительно ракеты, а не по скорости относительно инерциальной системы отсчёта).

Вводя вектор и учитывая, что , окончательно получаем:

.

27.12

Это математическое выражение называют уравнением Мещерского, а вектор - реактивной силой.

223

Реактивная сила – это сила, родственная той, которую ощущает стреляющий человек - при стрельбе из пистолета она ощущается кистью руки; при стрельбе из винтовки воспринимается плечом.

Мещерский Иван Всеволодович (1859-1935) уравнение 27.12 опубликовал в 1897 году. С 1902 г. заведовал кафедрой теоретической механики Петербургского политехнического института. Известен, прежде всего, как талантливый педагог - под его руководством коллективом кафедры в 1914 году издан неувядаемый «Сборник задач по теоретической механике» - переиздавался 36 раз, им пользуются не только у нас, но практически во всех странах мира.

27.7.3. Первая формула Циолковского (для одноступенчатой ракеты)

Для многих современных реактивных двигателей , где - максимально допускаемая конструкцией двигателя реактивная сила (тяга двигателя); - сила тяжести, действующая на двигатель, находящийся на земной поверхности (см., в частности, «Волков Е.Б. Ракетные двигатели.- М.: Воениздат, 1969.-105 с.»).

Тягу, большую чем , создать нельзя. Меньшую, вплоть до нуля, можно - например регулированием количества подаваемого в зону сгорания топлива. Но ясно, что с точки зрения дальности и быстроты полётов необходимо стремиться держать работу двигателя в режиме максимальной тяги.

К сожалению, если ракета предназначена для транспортировки людей, то ускорение не должно превышать 30 м/с² (подробнее с вопросом можно ознакомиться, например, в книге «Уманский С.П. Барьер выносливости лётчика.- М.: Машиностроение, 1964.-171 с.»). Но даже и в этом случае на поверхности Земли . С удалением же от Земли значимость гравитационной силы, по сравнению с тягой двигателя, уменьшается. Например, когда ракета поднимется от поверхности Земли на высоту, равную одному её радиусу, то сила её тяжести окажется уменьшенной в 4 раза; на высоте 2-х Земных радиусов над стартовой площадкой гравитационная сила Земли уменьшится в 9 раз. Задание студентам: из какого закона это следует?

Изложенное позволяет составляющей в уравнении Мещерского пренебречь и к дальнейшему анализу принять это уравнение в форме: ,

или, в проекции на направление вектора ,

224

а

27.13

.

Обозначаем:

- запас топлива (при жидкостных реактивных двигателях – это суммарная масса окислителя и горючего перед включением двигателя в работу);

- сухая масса ракеты (остающаяся её масса после выгорания всего топлива);

- масса отделившихся от ракеты частиц; расматривается как переменая величина, изменяющаяся от до .

Ясно, что масса ракеты (как переменная величина) определяется выражением:

б

Разворачивая (а) с учётом обозначений пункта 27.7.2, получаем:

.

Теперь подключаем связь (б) между дифференциалами и интегрируем:

,

где - характеристическая скорость – это скорость, которую приобретает ракета под действием тяги после извержения из ракеты всех частиц (при жидкостных реактивных двигателях – после выгорания всего топлива).

Вынесенная за знак интеграла (что можно делать на основании известной из высшей математики теоремы о среднем) - это средняя скорость извергаемых из ракеты частиц. Но, как видим, с точки зрения получения наибольшего значения характеристической скорости, должна быть как можно большей величиной. Поэтому на практике - это максимально достижимая скорость извержения частиц из ракеты. К сведению: в наиболее распространённых жидкостных реактивных двигателях (окислитель - жидкий кислород, азотная кислота, перекись водорода и др.; горючее - керосин, спирт, жидкий водород и т.д.) может достигать значений 3-3,5 км/с иногда до 4,5 км/с.

Итак,

225

Математическое выражение 27.13 называют первой формулой Циолковского (или: формулой Циолковского для одноступенчатой ракеты), где - число Циолковского.

Специалисты указывают, что вряд ли когда можно будет достичь .

Таким образом, в настоящее время при использовании одноступенчатых ракет можно лишь мечтать о достижении характеристической скорости км/с. Реально достижимая характеристическая скорость - км/с.

При выводе формулы Циолковского пренебрежено рядом факторов. В действительности получающаяся скорость, которую назовём конечной ( ), меньше характеристической:

27.14

где - гравитационные потери скорости (это компенсация неучёта действующей на ракету силы тяжести Земли);

- аэродинамические потери (трение о частицы воздушной среды); чтобы они были меньшими, ракеты стартуют в вертикальном положении; в этом случае плотные слои атмосферы они проходят по кратчайшему пути и на малых скоростях; аэродинамические потери намного меньше и ;

- потери на управление (нужно затратить горючее, чтобы вертикальное направление движения ракеты перевести на нужную траекторию).

Считается, что в современных ракетах суммарные потери не превышают 20%.

Каких же скоростей надо достигать, чтобы Человечество могло ставку делать на подготовку и осуществление космических полётов?

Чтобы ракета не смогла возвратиться на Землю (стала бы как и Луна спутником Земли, со средним расстоянием от земной поверхности в 200 км), необходимо достигать скоростей не менее 7,9 км/с, т.е. характеристическая скорость должна быть не меньшей км/с.

Как видим, одноступенчатая ракета не способна, по сегодняшнему уровню научно-технических достижений, преодолеть земное притяжение – неотвратимо будет возвращаться на земную поверхность. Но выход из положения есть!

226

2

Схема многоступенчатой ракеты

7.7.4. Вторая формула Циолковского

( для многоступенчатой ракеты)

Идея проста - зачем тратить топливо на разгон той части оболочки ракеты, в которой уже нет топлива? Её надо своевременно отсоединить от полезной части.

Схема многоступенчатой ракеты изображена на рис.27.7.

Ч

Рисунок 27.7

тобы не усложнять суть явления, но дать ему правильную качественную оценку, принимаем, что числа Циолковского одинаковы для всех субракет, одинаковы и относительные скорости изверже-ния частиц. Тогда скорость выводи-мого на космическую орбиту полезного груза:

после сгорания всего топлива в 1-й ступени - ;

после отработки 2-й ступени - ;

после отработки 3-й ступени - ;

и т.д.;

после отработки последней (К-ой) ступени:

27.15

.

Характеристики

Список файлов книги