ztm13 (850187), страница 4
Текст из файла (страница 4)
- записано на основании понятия центра тяжести, где 
- координата центра тяжести тела по оси 
. Но начинается в точке С и, поэтому, 
. Таким образом:
233
м
омент инерции тела относительно произвольной оси больше момента инерции этого же тела относительно параллельной ей центральной оси - на величину, равную произведению массы тела на квадрат расстояния между рассматриваемыми осями, т.е.
.
К моменту инерции стержня относительно перпендикулярной, прохо-дящей через конец, оси
ПРИМЕР 28.1.- Формула для вычисления момента инерции стержня относительно перпендикулярной, проходящей через конец, оси
Д Рисунок 28.6
ано. – Масса стержня 
, его длина 
(см. рис.28.6). Момент инерции стержня относительно перпендикулярной ему оси, проходящей через центр тяжести (относительно оси 
), определяется формулой: 
.
Требуется. - Вывести формулу для определения момента инерции стержня относительно перпендикулярной ему, проходящей через конец, оси.
Решение.- Используя формулу 28.8, получаем:
.
П
К моментам инерции треугольника
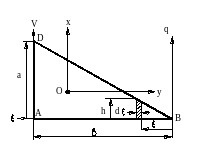РИМЕР 28.2.- Вывод формул для вычисления моментов инерции треугольника относительно различных осей Дано. – У однородного прямоугольного треугольника масса , а длины катетов 
и 
(как известно длина гипотенузы 
). 
- центр тяжести.
Т Рисунок 28.7
ребуется. - Вывести формулы для определения моментов инерции треугольника относительно изображённых на рис.7 осей, где 
- ось, дополняющая
и 
до правой прямоугольной системы координат.
Решение.- Вначале, воспользовавшись общей формулой 28.1, вычисляем момент
234
инерции треугольника относительно оси . Для этого треугольник разбиваем на элементарные полоски, параллельные осям 
. Одна из них изображена на рисунке: длина -
, толщина - 
, расстояние от оси - 
. Тогда:
, где
- толщина треугольника, 
- площадь и 
- объём элемента; 
- плотность материала, из которого выполнен треугольник. Учтём в преобразованиях, что (из подобия треугольников) 
. Таким образом:
, где
в круглых скобках – площадь треугольника; в квадратных скобках – его объём; в фигурных скобках – масса треугольника. Итак:
.
В
28.9
оспользовавшись двоекратно формулой, связывающей моменты инерции относительно параллельных осей, находим
и 
:
; 
.
В выражение для входит катет, перпендикулярный оси . Очевидно, поэтому, что 
.
.
Поясните: почему 
?
235
28.6. Формула для вычисления момента инерции относительно произвольно ориентированной оси
Н
Рисунок 28.8
К выводу формулы для момента инерции относительно произ-вольно ориентированной оси произ треугольника
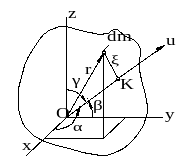а рис.28.8.- 
- произвольно связанная с телом М прямоугольная система координат; осевые и центробежные моменты инерции этого тела относительно осей (
; 
) известны. 
- проходящая через точку произвольно ориентированная ось (её орт 
), направляющие для неё углы (
) известны. 
- произвольная частица тела, 
- её радиус-вектор, - кратчайшее расстояние до оси .Сформулированную в заглавии раздела задачу решил ещё Эйлер – через углы, носящие его имя. Через направляющие косинусы, как рассматривается здесь, задачу впервые решил Коши (1827 г.). Вот эта зависимость:
.
С целью облегчения запоминания формулы, обращаем внимание на то, что она состоит из двух пар скобок; в первых скобках содержатся все произведения осевых моментов инерции на квадраты косинусов «своих» углов (
). Во вторых скобках содержится также сумма всех произведений центробежных моментов на косинусы своих углов (если 
, то косинусы углов 
и 
).
Докажем* справедливость формулы 28.9
а
.
Проектируем (а) на ось . Получаем:
236
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
