ztm11 (850185)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

П

К условию примеров 25.4 и 5

з

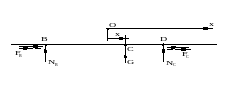
роанализировать её движение.

Р ешение.- Силы трения скольжения в точках В и D, как известно из статики, определяются по формулам:

а

(применительно к рассматриваемому случаю на рис. 5 они изображены сплошными стрелками).

П

Рисунок 25.4

К решению примеров 25.4 и 5

ренебрегая толщиной доски, из уравнений

и

п

25.12

олучаем (допустимость использова-ния записанных уравнений будет ясна после изучения принципа Даламбера):

б

;

в

Рисунок 25.5

Векторное уравнение, отображающее закон движения центра доски:

г

.

Проектируя его на ось , получаем:

д

.

Из (а), (б), (в) и (д):

е

, где

это уже встречавшаяся (см. 25.9) каноническая форма дифференциального уравнения свободных колебаний. Его решение:

ж

, где

постоянные определяем из начальных условий. Для этого учитываем, что

185

.

Откуда: и т.д.

Теперь используем (ж): .

Итак, получаем: , т.е. .

Замечание: из (е) видно, что механическую систему по рис. 4 можно использовать в качестве установки для определения коэффициента трения скольжения экспериментально-теоретическим способом – т.к. круговая частота с периодом колебаний связана соотношением , то получается

ф ормула для экспериментально-теоретического способа определе-ния коэффициентов трения скольжения

, где

м/с² – ускорение свободного падения, - конструктивный параметр; - экспериментально определяемый период колебания.

ПРИМЕР 25.5.- Доска на противоположно вращающихся барабанах. Силами трения растягивается - это пример на определение движения центра масс при силах, являющихся функцией координаты; характер движения неустойчивый. Вспомогательная значимость примера – показ на конкретном примере, что «подобия» и «похожести» по одним параметрам сопоставляемых систем (явлений, процессов и т.п.) далеко не всегда являются основаниями к утверждениям типа «да это тоже самое».

Дано. - Механическая система, рассматривавшаяся в примере 25.4 (изображена на рис.25.4 и 5) – та же конструкция ( м; вес доски - и прочие одинаковости); тот же коэффициент трения ( ), те же начальные условия (при м); причём, барабаны вращаются как и в примере 25.4 в противоположных направлениях, но произведен реверс электродвигателей - направления вращения для примера 25.5 указаны прерывистыми линиями.

Требуется проанализировать движение доски - возможность схода её с барабанов. И, если анализ предскажет такое событие, то вычислить момент времени , в который центр тяжести С доски будет проходить через точку D (или В) её соприкосновения с барабаном.

186

Решение.- Ясно, что решение примера 25.5 повторяет решение примера 25.4 до (г). Различия начинаются с (д) - получается

,

т.е. получается дифференциальное уравнение

е

, где .

Находим 1-й интеграл дифференциального уравнения (е).

Т.к.

,

то (е) принимает вид:

ж

.

И в левой, и правой частях видны табличные интегралы. Берём их -

з

Т.к. , то из (з): .

Вновь видим табличные интегралы. Интегрируем:

.

Из полученного уравнения движения видно монотонное возрастание с увеличением времени . Вывод: доска через определённый промежуток времени сойдёт с барабанов.

Вычисляем время , по истечении которого координата центра доски окажется равной половине (после чего она под действием собственного веса безвозвратно потеряет горизонтальное положение и свалится с барабанов):

187

.

Откуда с.

ПРИМЕР 25.6.- Вывод формулы для вычисления максимально возможной скорости катера. Это пример на определение движения центра масс в случае, когда главный вектор внешних сил является функцией квадрата модуля скорости

Дано. - Движущая катер сила (приложена к винту со стороны воды - рис.25.6) - .

К условию и решению

примера 25.6

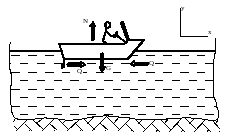- вес катера с людьми и прочим находящимся в нём грузом ( , где - масса, - ускорение свобод-ного падения тел). - выталкива-ющая сила. - сопротив-ление движению (со стороны воды); ; - модуль скорости катера. При .

О

Рисунок 25.6

пределить зависимость модуля скорости катера от времени –

Установить также максимально возможное значение этой скорости.

Решение.- Основное уравнение динамики материальной точки применительно к рассматриваемому случаю

.

Проектируем составленное векторное равенство на ось и получаем:

, где

.

В левой и правой частях получившегося дифференциального уравнения содержатся табличные интегралы. Интегрируя получаем:

188

Используя начальные условия находим постоянную и получаем:

Откуда, после алгебраических преобразований:

.

Из последнего выражения видно, что модуль скорости имеет максимальное значение при , т.е.

.

Решения примеров 25.3-6 требовало составления одного дифференциального уравнения второго порядка. Переходим к иллюстрации более сложных случаев - когда материальная точка имеет две степени свободы и приходится составлять систему двух дифференциальных уравнений 2-го порядка.

Ограничиваемся рассмотрением трёх близких друг к другу по инженерно-физической сущности случаев пассивного (без наличия движущей силы) полёта тела: пример 25.7 – без учёта сопротивления воздуха и два примера (25.8 и 25.9) - с учётом сопротивления.

189

ПРИМЕР 25.7.- Прыжок воднолыжника - это пример на определение движения центра масс в случае, когда главный вектор внешних сил является постоянной во времени величиной, движение криволинейное (в исторически значимых примерах, изложенных в поразделе 3.4, рассматривался более простой случай – прямолинейное движение).

Дано: начальная скорость ( ; м/с, ); высота ( м) расположения в начале полётной фазы центра масс механической системы «спортсмен-лыжи» над горизонтальной плоскостью, в которой этот центр масс окажется в момент касания лыж с водной поверхностью (см. рис.25.7).

Определить дальность ( ) и максимальную высоту полёта ( ) воднолыжника.

К условию и решению примера 25.7

Рисунок 25.7

Решение.- Записываем основное уравнение динамики материальной точки (центра масс системы «спортсмен-лыжи») применительно к рассматриваемому случаю

а

.

Проектируя (а) на ось получаем:

б

Откуда: .

Взяв второй интеграл от (б), получаем:

в

(постоянная интегрирования равнялась нулю по той причине, что время принято отсчитывать от момента, когда центр масс воднолыжника находится на оси ).

Теперь проектируем векторное равенство (а) на ось . Получаем:

190

г

.

При . Поэтому и:

д

.

Теперь интегрируем дифуравнение (д). Получаем:

.

Т.к. при то и, поэтому:

е

.

Момент времени, соответствующий обозначаем . В этот момент времени (потому, что вектор скорости на вершине траектории горизонтален).

Из математического анализа известно: чтобы установить максимум функции (а речь идёт о траектории) необходимо взять от неё производную и приравнять нулю. Такая производная уже имеется - см. (д), откуда и получаем:

ж

Теперь (ж) подставляем в (е) и получаем:

з

или, после числовой подстановки, м.

Момент касания лыжами водной поверхности ( ) устанавливаем из (е) -

т.к. при то получаем: .

Откуда (решая квадратное уравнение):

и

.

Теперь, после подстановки (и) в (в), получаем:

191

к

.

И, наконец, из (и) и (к) после численных подстановок находим:

м.

ПРИМЕР 25.8*.- Полёт тела (снаряда), брошенного под углом к горизонту с учётом сопротивления воздуха - это пример на определение движения центра масс в случае, когда главный вектор внешних сил является функцией вектора скорости

Дано. - Начальная скорость бросания ( - модуль, - угол её расположения относительно горизонта – см. рис. 25.8). Сила сопротивления , где - вес тела, - скорость его центра тяжести, - постоянная во времени величина (коэффициент).

Т

К условию и решению примера 25.8

ребуется Аналитически описать уравнение траектории центра тяжести тела – в форме .

Р ешение.- Основное уравнение динамики материальной точки применительно к рассматриваемому случаю:

.

Проектируем записанное вектор-ное уравнение на оси и :

а

б

И

Рисунок 25.8

з (а) : .

В левой и правой частях последнего выражения видим табличные интегралы. Интегрируя и используя начальные условия, получаем -

192

.

Интегрируем последнее выражение и используем начальные условия:

.

Откуда

и, поэтому:

в

.

Из (в) :

г

.

Из (г), после алгебраических преобразований:

д

.

Теперь интегрируем дифуравнение (б) :

.

После подстановки :

.

После переноса в правую часть, вновь видим табличные интегралы. После интегрирования получаем:

.

193

Используя начальные условия находим:

.

Поэтому

.

Подставляя в последнее выражение (г) и (д), окончательно получаем:

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги