ztm8 (850182)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

способа определения МЦС, устанавливаем, что мгновенным центром скоростей звена 2 является точка (МЦС₂ = ) и в соответствии с результатом 20.2 записываем:

б

.

Из (а) и (б):

в

,

причём, отображающая вектор круговая стрелка (см. рис20.7) совпадает с направлением, показывающим на циферблате часов ход стрелок (это направление видно из положения вектора относительно точки ).

Как и для : просто , т.е. просто .

см. (в) .

Для тела 4 известна траектория не только точки , но и (см. рис.7). Поэтому, используя 2-й способ определения положения МЦС, устанавливаем: МЦС₄ = . Откуда:

.

г

Направление круговой стрелки, отображающей вектор , устанавливаем по описанному (применительно к ) методу - см. рис.20.7.

Скорость точки записываем подходя с двух сторон (аналогично тому, как это было сделано для точки ):

см. (г)

.

145

П

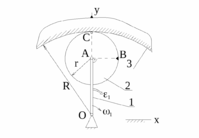
К условию и решению примера 20.2

РИМЕР 20.2.- Кинематического исследвание зубчато-рычажного механизма методом МЦС

Даны схема, геометрия и положение механизма - см. рис.20.8, где: 1 – рычаг (водило, стержень), шарнирно соединён-ный в точке с неподвижным телом, а в - с зубчатым колесом 2, имеющим внешнее расположение зубцов и подвижную ось вращения; 3 – неподвижное зубчатое колесо с внут-ренним расположением зубцов, с которым

с

Рисунок 20.8

цепляется зубчатое колесо 2 и центром которого является точка . см; см; ; .

Определить скорость и ускорение точки .

Решение.- В соответствии с 4-м способом МЦС₂ =

.

а

При разложении плоского движения тела 2 за полюс принимаем точку .

Учитывая закон о единой угловой скорости, делаем вывод: угловая скорость тела 2 относительно полюса определяется выражением (а) с той лишь корректировкой, что круговая стрелка, изображающая вектор , противоположна круговой стрелке, изображающей вектор , т.е.

,

б

Из (а) и (б), после подстановки числовых значений, получаем:

; .

Для определения скорости и ускорения точки применяем законы сложения (подобно тому, как делалось в примере 2 предыдущего раздела). Рекомендуем проделать это самостоятельно. Будет получено:

м/с; м/с².

146

20.7. Мгновенный центр ускорений. Пример использования этого понятия в кинематических исследованиях

Мгновенный центр ускорений (МЦУ) – это точка плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю.

Используя уже изложенные методы предлагаем самостоятельно доказать:

в любой момент времени, при одновременно не равных нулю угловых скорости и ускорения, плоско движущаяся фигура имеет один МЦУ, положение которого определяется формулами:

,

г

20.8

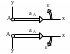
К определению положения МЦУ

де - модуль ускорения произволь-ной точки А этой фигуры; и - модули угловых скорости и ускорения;

о

Рисунок 20.9

сь начинается в точке А и сона-правлена с ; ось получается путём поворота, в плоскости фигуры (см. рис.20.9), на угол 90^о оси в направлении, указываемом круговой стрелкой, изображающей вектор ;

у

20.9

скорения точек плоской фигуры относительно МЦУ распределены таким образом, будто бы она в заданный момент времени вращается вокруг перпендикулярной ей, проходящей через МЦУ, оси, т.е. ускорения точек могут определяться по формулам 18.15.

Иллюстрация пред-остережения 20.10 МЦУ

Предостережение от распространённой ошибки:

М

20.10

Рисунок 20.10

ЦУ МЦС, т.е. мгновенный центр ускорений и мгновенный центр скоростей в общем случае не одна и та же точка на плоской фигуре. Так, для равномерно катящегося без проскальзываний по плоскости колеса мгновенным центром скоростей является точка его сопри-касания с плоскостью (см. рис. 20.10); мгновенным же центром ускорений является центр колеса – точка .

147

П

К условию примера 20.3

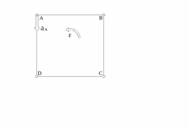РИМЕР 20.3.- На использование понятия МЦУ для определения ускорений вершин квадрата

Д

Рисунок 20.11

аны: ускорение точки квадрата (см. рис.20.8) - направлено от к и его модуль м/с²; угловое ускорение – направление указано на рисунке, модуль - ; модуль угловой скорости ; сторона квадрата - м.

Определить ускорения точек .

Р

К решению примера 20.3

ешение.- Вычисляем координаты МЦУ

м;

м.

Изображаем в масштабе заданный квадрат, на нём МЦУ (точку - см. рис.20.12) и непосредственными замерами из чертежа определяем:

.

В

Рисунок 20.12

соответствии с 20.9: ускорения всех точек квадрата ( ) отклонены от соответствующих радиус-векторов ( ) на одинако-

вые углы, в одном направлении (указываемом круговой стрелкой ) и определяемые из выражения . Модули ускорений рассматриваемых точек пропорциональны расстояниям от МЦУ ( ), т.е. получаем: м/с²;

м/с²; м/с².

148

21. Основные методы, используемые в кинематических исследованиях наиболее распространённых механизмов

21.1. Метод подчёркивания букв в векторных уравнениях

В сложных механических системах встречаются совпадающие друг с другом точки, принадлежащие различным телам и имеющие, поэтому, различающуюся кинематику. Для одной и той же точки скорости могут быть абсолютными, относительными и переносными, а ускорения ещё и нормальными, касательными, кориолисовыми. При применении опорных фактов кинематики весь комплекс этих величин даёт много различных, по форме близких, алгебраических комбинаций, из которых исследователю необходимо выбрать те, которые приводят к решению рассматриваемой им задачи. Отсутствие систематизированного, упорядоченного подхода приводит к умственным перенапряжениям и головным болям даже у опытных расчётчиков. Составление алгоритмов решения задач и пользование ими существенно облегчается, если использовать метод подчёркивания букв, отображающих векторные величины:

п

21.1

од изображающей вектор буквой пишется в два уровня по вертикали два символа - верхний и нижний; верхний содержит информацию об известности направления вектора; нижний - об известности модуля этого вектора; известность – горизонтальная чёрточка, неизвестность – косой крест. Если под буквой нет символов, это означает, что изображаемый ею вектор неизвестен ни по модулю, ни по направлению.

В дальнейшем вместо «прямая расположения вектора» в том же смысле будет употребляться более короткая фраза - «направление вектора».

П римеры: - скорость точки известна и по направлению, и по модулю;

- в отведенном месте есть запись о направлении ускорения точки, его же модуль неизвестен;

- модуль угловой скорости известен, направление - нет.

Применение метода рассмотрим на двух примерах.-

П

Механизм с качающейся направляющей для стержня

РИМЕР 21.1.- Кинематическое иссле-дование механизма с качающейся направляющей для стержня

Д

Рисунок 21.1

ано (см. рис.21.1): ; ; м; м; м;

; .

149

Пояснения к рис.21.1: сочленения тел 1 и 3 с корпусом механизма (с неподвижной системой отсчёта) таково, что эти тела могут совершать лишь вращательные движения; так же сочленены между собою тела 1 и 2; при этом, «вращательное движение» не следует понимать так, что одно тело относительно второго обязательно должно делать полный оборот (движение может быть и вращательно-колебательным); тела 2 и 3 сочленены иначе - так, что одно относительно второго может совершать лишь поступательное движение (говорят: «тела сочленены в поступательную пару»; при этом, тело 2 можно представлять в форме прямолинейного стержня, проходящего через сквозное отверстие в теле 3).

Определить угловые скорость и ускорение тела 3, а также скорость и ускорение точки относительно неподвижной системы.

Решение.- Абсоютной траекторией точки А является окружность радиуса АО с центром в точке О; следовательно АО (скорость касательна к траектории) и, судя по заданному , направлена влево-вверх, а её модуль:

=АО =0,05·100=5 м/с.

Итак,

а

АО , =5 м/с.

Задаёмся целью определить скорость точки В₂.

Для этого за подвижную принимаем поступательно перемещающуюся систему координат (см. рисунок), с началом совпадающим в функции времени с точкой А и, на основании закона сложения скоростей, записываем:

б

, где

(«4» - это номер тела, с которым связана неподвижная система отсчёта), т.е. - это абсолютная скорость точки В₂; обычно второй символ (в рассматриваемом случае «4») опускают, ибо для отличия абсолютной скорости (ускорения) от переносной и относительной односимвольный индекс оказывается более удобным;

- абсолютная скорость точки А;

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов книги