ztm8 (850182), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

- скорость точки В₂ относительно полюса А.

Траекторией точки В₂ относительно полюса А является дуга окружности радиуса ВА с центром в точке А. Следовательно:

150

в

ВА.

Используя 1 записываем:

;

г

Векторное уравнение (г) пока не решается (говорят: содержит 3 неизвестных - неизвестен ни по направлению, ни по модулю; неизвестен и модуль вектора ; решить уравнение можно лишь при 2-х неизвестных).

Временно оставляем его и переходим к поиску других уравнений.

Теперь за подвижную систему принимаем (связана с качающейся направляющей 3) и на основании того же закона сложения скоростей записываем:

, где

- абсолютная скорость точки В, принадлежащей телу 3. Эта точка неподвижна. Значит и последнее векторное равенство принимает вид:

.

Траекторией точки В₂ относительно тела 3 является отрезок прямой, параллельный оси (во времени расположенный на стержне АС). Следовательно:

д

АС

и уравнение (г) принимает вид:

.

е

Используя приём отрицательного модуля считаем, что , и, после проектирования (е) на оси и , получаем:

м/с;

м/с, т.е.

151

ж

м/с;

м/с;

з

и

; причём, поворот тела 2 виден происхо-

дящим в рассматриваемый момент времени по ходу стрелки часов.

Без дополнительных пояснений видно, что

к

; причём .

Скорость точки С находим вновь применяя закон сложения скоростей -

.

Скорость известна и по модулю, и по направлению - см. (а).

Теперь о .- Траекторией точки А относительно системы является дуга окружности радиуса АС с центром в точке А, т.е. АС; её модуль определяется по формуле вращательного движения - м/с. Итак,

л

м/с.

Получено векторное уравнение , имеющее две неизвестные.

С целью закрепления знаний решите его самостоятельно. Будет получено:

м/с, м/с.

Переходим к определению ускорений.

Тело 1 относительно неподвижной системы совершает вращательное движение. Поэтому:

и, в соответствии с формулами вращательного движения:

м/с²;

м

АО и направлен влево-вверх, м/с².

Т.е. имеем: .

152

На основании закона сложения ускорений:

; кориолисова ( ) составляющая ускорения равна нулю (т.к. подвижная система перемещается поступательно, что видно по символу «А»).

Т.к. траекторией точки В₂ относительно системы «А» является окружность радиуса ВА с центром в точке А, то:

н

; м/с²;

.

Пока полученное уравнение решить нельзя. Вновь используем закон сложения ускорений, но за подвижную теперь принимаем систему «3» - :

. О траектории точки В₂ относительно системы «3» уже писалось - отрезок прямой, параллельный оси (во времени расположенный на стержне АС). Поэтому

о

АС. (на основании изложенного в подразделе 19.3 правила Жуковского);

модуль же этого вектора:

м/с². Т.е.

.

Замечание:

д

21.2

ля ускорений кориолиса рекомендуем писать не просто , или и т.п., а ещё и указывать системы отсчёта - и т.д.

Необходимость делать это видна из рассматриваемого примера. В нём .

Возвращаемся к решению конкретной задачи. Видим: отдельно взятое векторное уравнение (о) как и (н) имеет 3 неизвестные и не может быть решено. Но решение появляется, если их объединить:

153

.

Метод проектирования векторного уравнения на оси встречался неоднократно. Проверьте его усвоенность самостоятельно, проведя соответствующие вычислительные операции. Будет получено: м/с².

После этого определяем угловое ускорение :

.

При этом получается, что круговая стрелка, изображающая векторы на плоскости, показывает направление противоположное ходу стрелок часов.

Ускорение точки С рекомендуем определить самостоятельно (как это делалось ранее). Будет получено:

( м/с²; м/с²).

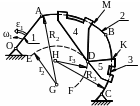
ПРИМЕР 21.2*.- На составление алгоритма кинематического исследования механизма с дугообразными направляющими

Дано: схема, геометрия и положение механизма, изображённого на рис.21.2. В момент времени, соответствующий заданному положению, известны угловые скорость ( ) и ускорение ( ) вращательно-колебательного движения тела 1.

Найти последовательность расчёта, целью которого является определение ускорений и . При этом, мы приведен лишь остов алгоритма. Студентам же рекомендуем дополнить его самостоятельным описанием направлений и модулей соответствующих векторов (подобно тому, как это делалось в примере 21.1), а полученные результаты обсудить, вскрывая свои, или товарищей-сокурсников, некорректности и, таким образом, установить истину.

Пояснения.- О, А, В, С и D - вращательные пары; кривая АВ - это дуга окружности с центром в точке G и радиусом R₂; кривая ВС - это дуга окружности с центром в точке H и радиусом R₃. Тела 2 и 4, 3 и 5 имеют скользящие соединения,- такие, что: траекторией точки D относительно тела 2 является дуга DE окружности с центром в точке G и радиусом ; траекторией точки D относительно тела 3 является дуга DF окружности с центром в точке H и радиусом .

154

Р

21.3

Схема механизма с дугообразными направляющими

екомендация: в состав-ляемых векторных урав-нениях удобно в правой части первой записы-вать относительную скорость (ускорение); это позволяет сразу видеть систему отсчёта, принятую за подвиж-ную, что и позволяет быстро записывать последующие векторы.

Р

Рисунок 21.2

ешение.- Для нахождения и вначале опреде-лим нужные скорости точек и тел.

.

; .

.

.

.

155

Переходим к ускорениям.-

.

.

; .

.

; .

.

.

156

21.2. Метод введения в рассмотрение систем отсчёта, превращающих подвижные оси вращения в неподвижные

Может использоваться для различных механизмов, но наибольшую значимость имеет для зубчато-рычажных. При этом, будущему инженеру, желающему видеть практицизм изучаемых им теорий, важно знать, что рабочие машины, в которых отсутствуют зубчатые передачи, встречаются редко.

С точки зрения кинематического анализа зубчатые передачи можно разделить на 2 класса.

Первый – оси вращения всех зубчатых колёс неподвижны; это так называемые рядовые их соединения, в кинематических исследованиях никаких трудностей не вызывающие – см. примеры 21.3 и 21.4.

Второй класс – зубчато-рычажные механизмы (планетарные, дифференциальные и др.); широко используются в общем редукторостроении, имеются практически в любом автомобиле и тракторе, во многих обрабатывающих станках, подъёмных и других машинах; их особенностью является наличие зубчатых колёс, оси вращения которых подвижны относительно корпусов механизмов.

Подробное ознакомление с зубчато-рычажными механизмами может быть начато с книги «Вулгаков Э.Б. Соосные зубчатые передачи. Справочник.- М.: Машиностроение, 1987.- 256 с.».

Кинематическое исследование зубчато-рычажных механизмов также оказывается несложным, если в рассмотрение введена осенесущая система отсчёта (такая, относительно которой оси вращения зубчатых колёс оказываются неподвижными).

С

21.4

уть метода.- Анализ движения начинают рассматривать с позиций наблюдателя, находящегося в осенесущей системе отсчёта. Это позволяет зубчато-рычажные механизмы (которыми они являются с позиций исследователя, находящегося в неподвижной системе отсчёта) превратить в рядовое соединение зубчатых колёс; их кинематическое исследование элементарно. Переход же от относительного движения к абсолютному осуществляется с помощью закона сложения угловых скоростей.

Приложение метода рассмотрим на двух примерах.

ПРИМЕР 21.3.- На пару вращений

Дано.- Схема зубчато-рычажного механизма (см. рис.21.3): слева - главный вид, посередине – вид сбоку; 1 – неподвижное, 2 и 3 подвижные зубчатые колёса; 4 – рычаг (иначе: водило), имеющий 3 оси вращения (О, А, В) для зубчатых колёс.

157

. Справа на рис.21.3 изображён рассматриваемый механизм с позиций исследователя, мысленно поместившего себя в системе отсчёта, связанной с водилом ОАВ.

Зубчато-рычажный механизм, иллюстрирующий пару вращений

Рисунок 21.3

Установить зависит ли угловая скорость зубчатого колеса 3 от угловой скорости водила 4. И если зависит, вывести соответствующую формулу.

Решение.- - угловые скорости 1-го, 2-го и 3-го зубчатых колёс относительно водила (относительно системы отсчёта, в которой оси вращения оказываются неподвижными). Из примеров 18.3 и 18.4 с очевидностью следует:

.

Т.к. , то

Теперь, 2 раза задействовав закон сложения угловых скоростей, получаем:

,

т.е. 3-е зубчатое колесо относительно неподвижной системы отсчёта совершает поступательное движение - для него .

С

21.5

ложное движение тела, складывающееся из 2-х вращений, таких, что относительная угловая скорость противоположна переносной и равна ей по модулю, называют парой вращений. У пары вращений абсолютным движением является поступательное.

158

П

Принципиальная

схема привода ведущих колёс автомобиля

РИМЕР 21.4.- Кинематическое исследование конического дифференциала автомобиля

Н а рис.21.4: 1 – рама автомобиля; 2 – двига-тель с коробкой передач, приводящий во вращение карданный вал 3 (который имеет 2 шарнира Гука); 5 – конический дифференциал, приводящий во вращение правое (4) и левое (6) ведущие колёса.

Н

Рисунок 21.4

а рис.21.5, являющимся кинематической детализацией рис.21.4, изображено: 1 – корпус диффе-ренциала (неподвижен относительно рамы автомобиля); 3 – коническая шестерня, приводимая во вращение карданным валом; 4 – правое и 6 – левое ведущие колёса (приводятся в движение одинаковыми коническими колёсами, которым присвоены те же номера - 4 и 6); 7 и 8 – сателлиты

Кинематические связи конического дифференциала

Характеристики

Список файлов книги