ztm7 (850181)
Текст из файла
ж
.Подставляя (ж) в (е) и учитывая первое равенство из (б), получаем:

з

и
Взяв от последнего равенства производную по времени с позиций наблюда-теля, находящегося в неподвижной системе, и учитывая (г), (д), (з), (и), получаем:
19.2
- формула, связываю-щая между собою абсолютную и относительную скорости точки. Математическое выражение 19.2 рассматривается как функция времени. Однако в расчётную практику в большей степени вошёл подход, в соответствии с которым каждому моменту времени соответствует своя точка Е – такая, с которой совпадает точка М. В этих случаях ![]() и 19.2 принимает вид:
и 19.2 принимает вид:
19.3
; (иначе -19.3. Закон сложения ускорений
С позиций наблюдателя, находящегося в неподвижной системе отсчёта, берём производную по времени от математического выражения 2. Получаем:
к
л
.129
Вспомогательная система относительно неподвижной перемещается поступательно. Следовательно

м
относительно вспомогательной.
Теперь, учитывая (з) и (и), преобразуем последнее слагаемое выражения (к):
19.4
связывающая абсолютное и относительное ускорения точки.
Подобно скоростям в расчётную практику вошёл подход, в соответствии с которым каждому моменту времени соответствует своя точка Е – такая, с которой совпадает точка М. В этих случаях ![]() и 19.4 принимает вид:
и 19.4 принимает вид:
и
19.5
наче:формула, выражающая закон сложения ускорений;
![]() называют кориолисовой (или поворотной) составляющей абсолютного ускорения. Густав Кориолис (1792-1843) –
называют кориолисовой (или поворотной) составляющей абсолютного ускорения. Густав Кориолис (1792-1843) –
французский математик и механик; опубликовал результат 19.5 в 1831 году.
Замечание.- При исследовании динамических процессов иногда используют третьи производные от радиус-векторов, называя их «рывками» («пульсами», «ускорениями 2-го порядка»). В частности, специалисты пишут: «При исследовании колебаний в механизмах нередко существенную роль играет интенсивность изменения ускорений».
Взяв производную по времени от 19.4, получаем теорему сложения пульсов:
Главные цели её приведения: демонстрация преимуществ изложенного теоретического метода над аналогичными другими известными и, главное, в пояснении различия между понятиями «закон» (сложения ![]() ) и «теоремой» - результат назван теоремой потому, что сегодня он лишь предсказание, почти с достоверностью правильное, но пока новое и не общепризнанное.
) и «теоремой» - результат назван теоремой потому, что сегодня он лишь предсказание, почти с достоверностью правильное, но пока новое и не общепризнанное.
130
П
К переплыванию реки

абсолютная
траектория
пловца
финиш
пассивно
плывущий
предмет
старт
B
V
a
A
r
V
e
V



































































































































































































































































 РИМЕР 19.1.- На закон сложения скоростей – переплывание реки
РИМЕР 19.1.- На закон сложения скоростей – переплывание реки Д
Рисунок 19.3
ано.- Туристической группе необходимо вплавь перебраться на выбранную на противоположном берегу реки площадку (на рис.19.3 точка В), но при этом недопустим выход из воды ниже этой точки (например, по той причине, что ниже запримеченной площадки в реку впадает её приток). При этом известно, что наименее подготовленный представитель туристической группы в бассейне (или озере) может плыть со скоростью 30 м/мин.Определить точку А вхождения туристов в воду (через угол ![]() , под которым траектория АВ плывущих туристов пересекает среднюю линию русла реки).
, под которым траектория АВ плывущих туристов пересекает среднюю линию русла реки).
Решение.- Отмеряют на береговой линии отрезок, параллельный средней линии русла реки. Длиной, например, 50 м и устанавливают время, в течение которого пассивно плывущие по реке предметы преодолевают этот путь. Положим скорость течения реки (среды, переносящей вместе с собой тело пловца) оказалась равной 20 м/мин.
Берега реки принимаются за неподвижную систему отсчёта, а водная среда, вместе с находящимися в ней ветками, щепой и палками, за подвижную систему.
Т
К решению примера 19.1
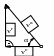 огда 20 м/мин и 30 м/мин – это модули соответственно переносной
огда 20 м/мин и 30 м/мин – это модули соответственно переносной На основании закона сложения строим треугольник
скоростей (рис.4) и устанавливаем: ![]() .
.
И
Рисунок 19.4
з подручных материалов (например из ивовых прутьев) изготавливают прямоугольный треугольник, длины катетов которого относятся между собою как 3 к 2-м. При установлении положения точки А его держатгоризонтально, причём так, чтобы меньший катет был параллелен средней линии русла реки, а второй перпендикулярен ей и, идя вдоль берега, наблюдают за положением гипотенузы – место, в котором находится треугольник, когда точка В оказывается на содержащей гипотенузу прямой и есть искомая точка А.
131
П
Движущийся вагон с вращающимся в нём стержнем
РИМЕР 19.2.- На закон сложения ускорений; подвижная система перемещается поступательноД ано.- В изображённом на рис.5 положении (
ано.- В изображённом на рис.5 положении (![]() ):
): ![]() ;
; ![]() м/с;
м/с; ![]() м/с2; АО=1 м.
м/с2; АО=1 м.
Определить абсолютное (относительно системы ![]() ускорение точки А.
ускорение точки А.
Решение.- Воспользуемся законом сложения ускорений:
Рисунок 19.5
,За подвижную систему координат принима-
ем ![]() , которая, как видно из рисунка (из условия), перемещается поступательно относительно неподвижной
, которая, как видно из рисунка (из условия), перемещается поступательно относительно неподвижной ![]() .
.
Т.к. подвижная система координат перемещается поступательно, то ускорения всех её точек одинаковы и, поэтому, переносная составляющая (![]() ) ускорения точки А равна указанному на рисунке
) ускорения точки А равна указанному на рисунке ![]() .
.
Относительно подвижной системы точка А движется по окружности радиуса АО с центром в точке О. Поэтому относительную составляющую ускорения целесообразно представить двумя векторами -
![]() , которые определяются как при простом вращательном движении:
, которые определяются как при простом вращательном движении:
К решению примера 19.2
м/с2a
e





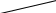












 м/с2;
м/с2; Г




 рафически решая (см. рис. 6) полу-
рафически решая (см. рис. 6) полу-
Рисунок 19.6

 м/с2; направлен же вектор абсолютного ускорения точки А влево-вниз под углом 11о к горизонтали.
м/с2; направлен же вектор абсолютного ускорения точки А влево-вниз под углом 11о к горизонтали. 132
П
Ускорение точки,
движущейся по вращающемуся кольцу
РИМЕР 19.3.- На закон сложения ускорений – с кориолисовой составляющейД ано.- Четверть кольца радиуса
ано.- Четверть кольца радиуса ![]() м скреплена со стержнем, вращающимся вокруг оси
м скреплена со стержнем, вращающимся вокруг оси ![]() (см. рис.19.7, где выше расположен главный вид, под ним – вид сверху). В интересующий момент времени:
(см. рис.19.7, где выше расположен главный вид, под ним – вид сверху). В интересующий момент времени: ![]() ,
, ![]() м;
м; ![]() м/с;
м/с; ![]() м/с2;
м/с2; ![]() ;
; ![]() . Направления векторов
. Направления векторов ![]() ,
, ![]() ,
, ![]() и
и ![]() указаны на рисунке.
указаны на рисунке.
Определить для заданного момента времени проекции абсолютного ускорения точки М на оси неподвижной системы отсчёта.
Р
Рисунок 19.7
ешение. – За подвижную принимаем систему отсчёта, связанную с вращающимся телом и применяем теорему сложения ускорений –Т.к. относительной траекторией точки М является дуга окружности (радиуса ![]() м с центром в точке В), то
м с центром в точке В), то ![]() представляем в виде нормальной и касательной составляющих -
представляем в виде нормальной и касательной составляющих - ![]() и
и ![]() ; первая направлена от В к М; вторая – по касательной в точке М к указанной относительной траектории. Их модули:
; первая направлена от В к М; вторая – по касательной в точке М к указанной относительной траектории. Их модули:
Переносной траекторией точки М (абсолютной траекторией той точки подвижной системы, с которой в рассматриваемый момент времени совпадает точка М) является окружность с центром в точке А и радиусом ![]() м.
м.
Переносное ускорение также представляем в виде двух составляющих - ![]() и
и ![]() ; первая направлена от М к А (по главной нормали к переносной траектории), вторая - по касательной к ней в сторону зрачка читателя (что видно по круговой стрелке, изображающей вектор углового ускорения
; первая направлена от М к А (по главной нормали к переносной траектории), вторая - по касательной к ней в сторону зрачка читателя (что видно по круговой стрелке, изображающей вектор углового ускорения ![]() ). Их модули:
). Их модули:
Переходим к определению кориолисова ускорения - ![]() .
.
133
Направление вектора ![]() можно определять по известным из курса математики правилам векторного произведения, но более удачным считается
можно определять по известным из курса математики правилам векторного произведения, но более удачным считается
п
19.6
равило Жуковского: чтобы определить направление кориолисовой составляющей ускорения, нужно вектор относительной скорости (Жуковский Н.Е. (1847-1921) – выдающийся отечественный учёный, известен основополагающими работами в области аэродинамики; его «Теоретическая механика» являлась базовым курсом первую половину 20-го века.
В рассматриваемом примере вектор кориолисова ускорения оказался противоположно направленным оси ![]() (см. рисунок). Его модуль:
(см. рисунок). Его модуль:
Итак, в рассматриваемой задаче полное ускорение оказалось представленным в виде 5-ти составляющих:
Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.




 ;
;
















