ztm7 (850181), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

.

Решаем его аналитическим способом - путём проектирования на оси :

м/с²;

510 м/с²;

.

Итак, абсолютное ускорение точки М в заданный момент времени (в заданном положении механической системы) перпендикулярно оси и его проекции на оси и равны: м/с²; 510 м/с².

19.4. О главном подходе к кинематическому исследованию сложно движущихся тел

Главный подход к кинематическому исследованию сложно движущихся тел заключается в разложении сложного движения на простые и применение законов сложения скоростей, ускорений. Обратной задачей является синтез сложных движений из простых. Комбинаций в разложениях и сложениях движений можно

134

придумать много; особенно если пойти по методу «матрёшка в матрёшке» – с введением в рассмотрение понятия «подвижная система -го уровня» (подвижная система 1-го уровня – это система, движение которой определено относительно неподвижной системы отсчёта; подвижная система 2-го уровня – это система, движение которой определено относительно подвижной системы 1-го уровня; подвижная система 3-го уровня – это система, движение которой определено относительно подвижной системы отсчёта 2-го уровня; и т.д.; пример этому см. в разделе 22). Но такой подход имеет больше теоретическую, нежели практическую значимость.

Из описанного множества возможных вариантов инженерный интерес представляют: сложение поступательных движений; винтовое, плоскопараллель-ное и свободное движения; сложение вращений. Рассмотрению этого круга вопросов, с акцентом на ещё не излагавшихся методах и значимых фактах кинематики и уделим дальнейшее внимание.

При этом, будем иметь ввиду, что сложение поступательных движений и винтовое движение оригинальности и сложностей не содержат – для их исследования достаточно уже изученных кинематических фактов и методов. Поэтому ограничиваемся лишь краткой о них информацией:

если складываются поступательные движения, то результирующим будет также поступательное движение;

винтовое движение - это движение, получающееся в результате сложения поступательного (со скоростью ) движения с вращательным, ось которого содержит вектор ; при - движение называют правовинтовым; при - левовинтовым; обычно , называют ходом винта.

Инженер часто встречается с необходимостью разлагать на простые свободное и плоское движения тел. Рассмотрим этот вопрос подробнее.

Свободное движение представляется суммой поступательного и сферического, плоскопараллельное – суммой поступательного и вращательного.

Термин «свободное (произвольное) движение» понятен без дополнительных пояснений. О втором этого сказать нельзя. Поэтому: плоскопараллельное (синоним: плоское) - это такое движение тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Примеры плоскопараллельных движений: колёса транспортных средств (поездов, автомобилей и т.д.) на прямолинейных участках дорог; движение вагона в метро (с учётом поворотов).

Применяя метод, использованный для показа равенства скоростей и ускорений точек поступательно движущегося тела, видим:

135

е

19.7

сли тело совершает плоскопараллельное движение, то у любого его отрезка, расположенного перпендикулярно неподвижной плоскости, скорости (и ускорения) точек равны между собой, т.е. кинематика плоскопараллельного движения тела сводится к кинематике плоской фигуры, скользящей по неподвижной плоскости.

Рассмотрим вопрос о числе степеней свободы плоской фигуры.-

Н

О числе степеней

свободы плоской фигуры

Рисунок 19.8

z

y

x

y

C

x

y



а рис.19.8: - система отсчёта, поступательно перемещающаяся относительно неподвижных осей и начало которой во времени совпадает с какой-либо точкой плоской фигуры (обычно за точку , особенно в динамике, принимают центр тяжести). Как видим, число степеней свободы плоской фигуры (число независимых переменных, однозначно определяющих её положение относительно системы ) равно трём - абсцисса и ордината точки , а также угловая координа-

та (определяющая положение плоской фигуры во вращательном её движении относительно подвижной системы ).

П

К свободному

движению тела

z

y

x

x

z

y

M

O



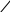
лоское движение является частным случаем свободного. По этой причине вводимые в этом подразделе кинематические факты будем формулировать применительно к свободному движению тела. Что же касает-ся иллюстрирующих примеров, то больше внимания будет уделено чаще встречающе-муся плоскому движению.

П

Рисунок 19.9

усть тело относительно непод-вижной системы (см. рис.19.9) совершает произвольное движение. Берём систему , поступательно перемещающуюся относительно и совмещаем её начало во времени с какой-либо точкой О этого тела.

О называют полюсом. Очевидно, что:

136

п

19.8

оложение произвольно движущегося тела определяется двумя тройками координат - абсциссой, ординатой, аппликатой полюса и углами Эйлера, определяющими сферическое движение тела отно-сительно подвижной системы, поступательно перемещающейся относительно неподвижной и начало которой совмещено с какой-либо точкой этого тела. Говорят - «произвольно движущееся тело имеет 6 степеней свободы».

Вместо длинного «сферическое движение тела относительно системы отсчёта, перемещающейся поступательно относительно неподвижной и начало которой совмещено с какой-либо точкой этого тела» обычно говорят - «сферическое движение относительно полюса», но следует помнить: «полюс» - понятие большее, чем «точка»; это точка тела с привязанной к ней своим началом поступательно перемещающейся системой отсчёта.

На основании законов сложения, с учётом принимавшихся условностей в обозначениях,

с

19.9

корость и ускорение любой точки М произвольно движущегося тела могут определяться по формулам:

,

где при свободном движении определяются формулами сферического, а при плоском – формулами вращательного движения (кориолисово ускорение отсутствует по причине поступательного перемещения подвижной системы отсчёта).

Инженеры в исследованиях широко используют законы о проекциях скорос-тей точек тела на проходящую через них прямую, о единой угловой скорости тела (о независимости угловой скорости от точки тела, принимаемой за полюс) и сложения угловых скоростей. Их рассмотрением и завершим 19-й раздел.

19.5. Закон о проекциях скоростей точек тела на проходящую через них прямую:

п

19.10

роекции скоростей любых двух точек тела на проходящую через них прямую равны.

Теоретический переход от предыдущего материала к закону 19.10 позволяет сделать метод проектирования векторного уравнения на ось. И действительно, пусть и - две произвольные точки свободно движущегося тела.

Приняв за полюс получаем (см. 19.9): , где , как скорость в сферическом движении тела относительно системы , определяется по формуле .

137

Т.к. , то, после проектирования на направление векторного равенства , получаем 19.10.

19.6. Закон о независимости угловой скорости тела от выбора полюса

(закон о единой для тела угловой скорости):

у

19.11

гловая скорость сферической составляющей свободно движущегося тела не зависит от принятой за полюс точки.

И

К закону о единой для тела

угловой скорости

зложим метод, позволяющий теоретическим путём прийти к закону 19.11.

П усть , и - три произволь-ные точки тела . и поочерёдно принимаем за полюса (с системами отсчёта соответственно и - рис.19.10). В соответствии с 19.9 записываем:

а

;

Рисунок 19.10

б

;

.

в

Из (а) и (б): .

Из (в): .

Из последних двух равенств:

.

г

При рассмотрении сферического движения угловая скорость вводилась как количественная характеристика, не зависящая от частиц тела, т.е. и - это одинаковые для всех номеров частиц векторы.

же - это переменный вектор, отражающий в себе множество векторов различных направлений (ввиду произвольности выбора точек в теле).

Таким образом, равенство нулю (г) имеет место не по причине параллельности векторов и , а потому, что .

138

19.7. Закон сложения угловых скоростей

Н

К закону сложения

угловых скоростей.

Постановка вопроса

угловой скорости

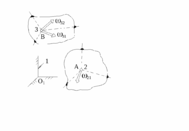а рис.19.11: 1, 2 и 3 - неподвижное и произвольно движущиеся тела. Рассматри-ваем их как 3 разные системы отсчёта - как совокупности точек, не препятствующих взаимным перемещениям; - угловая скорость тела 2 в сферическом его движении относительно системы отсчёта, поступательно перемещающейся по отношению к системе 1, начало которой во времени совпадает с точкой тела 2;

Рисунок 19.11

- угловая скорость тела 3 в сфери-ческом его движении относительно системы отсчёта, поступательно перемещающейся по

отношению к системе 2, начало которой во времени совпадает с точкой тела 3;

- угловая скорость тела 3 в сферическом его движении относительно системы отсчёта, поступательно перемещающейся по отношению к системе 1, начало которой во времени совпадает с точкой тела 3.

Характеристики

Список файлов книги