ztm7 (850181), страница 3
Текст из файла (страница 3)
Называют: 
, 
, 
- абсолютной, относительной и переносной угловыми скоростями тела 3. Как они связаны между собою?
На этот вопрос отвечает закон сложения угловых скоростей:
19.12
; иначе -
- абсолютная угловая скорость тела равна геометрической сумме относительной и переносной её составляющих.
Замечание: математическая запись закона 19.12 идентична той, которая в подразделе 19.2 отображала закон сложения линейных скоростей - 
. Но чтобы была видна разница в механической сущности применены различные буквы - 
и 
.
Теоретический переход от предыдущего материала к закону 19.12 можно основать на законах 19.11 и 19.3, используя ранее рассматривавшиеся методы. Покажем это.-
З
К закону сложения угловых скоростей. Картина после преобразований
акон о единой для тела угловой скорости позволяет перейти к другим принимаемым за полюса точкам тел 2 и 3:
заменяем полюсом 
( - точка тела 2, совпадающая в принятый к рассмотрению момент времени с нача-139
л
К закону сложения угловых скоростей. Картина после преобразований
ом
неподвижной системы отсчёта), а два полюса 
заменяем двумя полюсами 
( - точка тела 3, совпадающая в принятый к рассмотрению момент времени с началом 
неподвижной системы отсчёта; одна система с началом в точке перемещается поступательно относительно первой системы отсчёта; вторая система с началом в точке перемещается поступательно относительно системы отсчёта 2).В
результате проведенных преобразований получаем картину, представленную на рис.19.12, где буквой 
отображены 2 совпадающие в принятый к рассмотрению момент времени точки, одна принадлежит телу 2 (
), вторая - телу 3 (
).
По формулам сферического движения записываем:
,
Рисунок 19.12
,
.
Теперь используем закон сложения линейных скоростей -
.
Подставляя в последнее выражение 3 предыдущих, получаем:
.
- произвольная точка. Это значит, что 
может иметь любое направление. Поэтому равенство нулю обеспечивается не параллельностью векторов 
и , а тем, что 
.
Откуда и следует результат 19.12.
Закон сложения угловых скоростей широко применяется в инженерной практике – для кинематического исследования зубчато-рычажных механизмов (планетарных, дифференциальных и пр.) - см. подраздел 21.2.
140
20. О кинематических исследованиях
плоско движущихся тел и их соединений
методами мгновенных центров скоростей и ускорений
20.1. О существовании мгновенного центра скоростей
Мгновенный центр скоростей (МЦС) - это точка плоской фигуры, скорость которой равна нулю.
Из ранее рассмотренных методов (в числе которых проектирование векторного равенства на ось) вытекает следующий кинематический факт:
в
20.1
любой момент времени при не равной нулю угловой скорости плоско движущаяся фигура имеет один мгновенный центр скоростей.И
О существовании МЦС
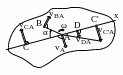действительно, пусть (см. рис.20.1) - одна из точек плоской фигуры; такая, что в рассматриваемый момент времени её скорость (
) не равна нулю. Из , перпендикулярно , проводим ось 
. Пусть, далее, - другая, не расположенная на оси , точка этой же плоской фигуры.З
Рисунок 20.1
а полюс принимаем точку . Тогда 
, где 
(т.к. 
), причём 
и, следовательно, проекция этого вектора на ось не равна нулю.
Спроектировав составленное векторное равенство на ось , получаем: 
, т.е. 
и если МЦС есть, то он может находиться лишь на оси .
Пусть теперь 
является произвольной, не совпадающей с , точкой оси . Тогда: 
, где 
, причём вектор 
и, следовательно, 
(сонаправлен, либо противоположно направлен 
: по одну сторону от точки - 
, по другую - 
).
Ясно, что если и есть МЦС, то надо смотреть те точки оси , для которых 
(на рис.1 этим множеством точек является полуось, начинающаяся в и сонаправленная с вектором 
).
141
может иметь любую величину (от нуля до бесконечности). И в этом множестве нет повторяющихся значений, но по причине непрерывности, будет присутствовать значение, для которого 
и, поэтому, 
. Т.е. МЦС есть; и он один.
Итак, применяемые методы приводили ранее к правильным, хорошо проверенным результатам, привели к этому и в рассмотренном случае.
2
Картина распределения скоростей точек плоской фигуры
0.2. О распределении скоростей относительно МЦСС
20.2
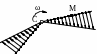корости точек плоской фигуры относительно МЦС распределены таким образом (см. рис.2), будто бы она в заданный момент времени вращается вокруг перпендикуляр-ной ей, проходящей через МЦС, оси, т.е. скорости точек могут определяться по формуле 18.13 - 
.Р
Рисунок 20.2
езультат 20.2 прямо следует из подраздела 20.1.20.3. Основные способы определения положений МЦС
К 1-му способу опреде-ления положения МЦС
Первый способ (см. рис.20.3):
е
Рисунок 20.3
20.3
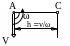сли известны угловая скорость (
) плоской фигуры и скорость (
) одной из её точек ( ), то для определения положения МЦС можно воспользоваться следующей последовательностью действий: изобразить на фигуре заданную точку с приложенной к ней скоростью ; затем вектор повернуть на 90о вокруг его начала в сторону вращения фигуры и вполученном направлении от заданной точки отложить отрезок 
; его концом и окажется МЦС
(как и 20.2 результат 20.3 виден из рассуждений, проведенных в подразделе
20.1).
142
В
Ко 2-му способу опреде-ления положения МЦС
торой способ (см. рис.20.4):е
20.4
сли у плоской фигуры известны прямые расположения скоростей двух точек, то их надо повернуть в плоскости фигуры вокруг заданных точек на 90о; пересечение 
и является искомым МЦС; в
Рисунок 20.4
К 3-му способу опреде-ления положения МЦС
торой способ прямо следует из тех уже установленных фактов, что скорость точки перпендикулярна радиус-вектору и плоская фигура имеет лишь один МЦС.Третий способ (см. рис.20.5):
е
20.5
сли скорости точек плоской фигуры параллельны и не равны, то её МЦС находится на пересечении ( ) прямых, одна из которых проходит через начала, вторая через концы заданных скоростей.Р
Рисунок 20.5
езультат 20.5 прямо следует из 20.2. Причём, если всё делается корректно, то ясно, что проходящая через заданные точки прямая перпендикулярна скоростям.Ч
К 4-му способу опреде-ления положения МЦС
етвёртый способ (см. рис.20.6):М
20.6
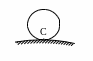ЦС катящегося без проскальзы-вания колеса находится в точке его соприкосновения ( ) с неподвижной поверхностью.20.4. Начальные сведения о центроидах
М
Рисунок 20.6
гновенный центр скоростей потому и «мгновенный», что с течением времени изменяет своё положение.Геометрическое место МЦС на плоской фигуре называют подвижной центроидой.
Ту точку неподвижной плоскости, в которой в рассматриваемый момент времени расположен МЦС, называют мгновенным центром вращения.
Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой.
143
Понятия подвижной и неподвижной центроид широко используют в теории зубчатых зацеплений, где, в частности, доказывается, что «подвижная центроида обкатывается по неподвижной без скольжения».
20.5. О мгновенном поступательном движении плоской фигуры
Из аксиомы о гладкости траекторий (с.95) и из связи между линейными и угловыми скоростями с очевидностью следует: угловые скорости являются плавно изменяющимися во времени величинами, т.е. при изменении направления вращения плоской фигуры её угловая скорость обязательно проходит через нуль.
Ту бесконечно малую во времени часть плоского движения, когда угловая скорость фигуры бесконечно мало отличается от нуля, называют мгновенным поступательным движением. Из рассмотренного в подразделах 20.1 и 20.2 с очевидностью следует:
п
20.7
ри мгновенном поступательном движении все точки плоской фигуры имеют одинаковые скорости, а её МЦС расположен в бесконечности.20.6. Примеры кинематического исследования простых плоских механизмов с использованием понятия МЦС
П
К условию и решению примера 20.1
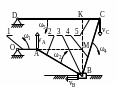РИМЕР 20.1.- На использование понятия МЦС для определения угловой скорости ведомого звена простого пятизвенного стержневого механизма Даны схема, геометрия и положение механизма (см. рис.20.7): 
; 
см; 
см; 
см; 
см; 
см; 
см.
Определить угловую скорость тела 5.
Р
Рисунок 20.7
ешение.- Будем иметь ввиду, что
просто , причём 
в функ-ции времени, т.е. 
просто . Модуль скорости точки : 
а
. Находим мгновенный центр скоростей для звена 2. Для этого, используя очевидность траекторий точек и , устанавливаем их скорости: 
направлена вертикально вверх, 
горизонтально. Тогда, на основании 2-го
144
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
