ztm13 (850187), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

Это и есть вторая формула Циолковского (для многоступенчатой

ракеты),

из которой, в частности, видно: при км/с.

Этой скорости уже достаточно не только для того, чтобы космическому аппарату уйти из сферы притяжения Земли и стать планетой Солнца; достаточно и для того, чтобы землянин смог улететь за пределы Солнечной системы (о трёх космических скоростях речь будет вестись в подразделе 33.7).

227

28. Массо-геометрические характеристики твёрдых тел

28.1. Введение в раздел

Здесь вводятся, взаимосвязываются и исследуются механические величины, через которые в последующем выражаются очередные опорные факты теоретической механики, т.е. с точки зрения формулируемых механических результатов излагаемый материал является вспомогательным. Но большой объём и востребованность для различных опорных фактов теоретической механики делает целесообразным его выделение в отдельный раздел.

Подробно ознакомиться с массо-геометрическими характеристиками можно в книгах: «Фаворин М.И. Моменты инерции тел: Справочник.- М., 1970.- 312 с.» и «Гернет М.М., Ратобыльский В.Ф. Определение моментов инерции.- М.: Машиностроение, 1969.- 247 с.». Здесь же (в «Курсе») ограничиваемся введением в вопрос, ознакомлением с основными применяемыми методами и чаще других встречающимися результатами.

2

1

8.2. Об инженерно-физической сущности рассматриваемых вопросов

Н

К вопросу о влиянии геомет-рии масс на кинематику механических систем

с текучей средой

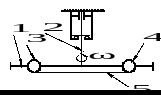а рис.28.1 изображена схема устрой-ства, доступная для изготовления студентами:

1 - стержень, вращающийся с угловой скоростью вокруг вертикальной оси 2; 3 и 4 –свободно надетые на него шары с отверстиями; 5 – зажигающаяся от пламени нить (например, хлопчатобумажная).

Е

Рисунок 28.1

сли к нити поднести пламя зажжённой спички, она перегорит, шары удалятся от оси вращения (до упоров) и явно («на глазок») будет видно, что угловая скорость стержня заметно уменьшилась.

Подобное механическое явление можно наблюдать и на экране телевизора: а) на ледовой площадке спортсмен-фигурист, чтобы достичь высокой угловой скорости соединяет ноги, выпрямляет туловище и вытягивает вверх руки, с целью же гашения скорости (в конце выступления) руки разбрасывает по сторонам; б) чтобы успеть сделать двойное, а часто и тройное сальто, спортсмен сжимается в комочек.

Из приведенных примеров видно, что на кинематику механической системы оказывают влияние не только массы, но и взаимное их расположение.

228

28.3. Основные массо-геометрические характеристики твёрдых тел

и общие формулы для их вычисления

Н

К понятиям о моментах инерции тел

а рис.28.2: - произвольная, связанная с твёрдым телом декартова прямоугольная система координат;

- масса произвольной частицы этого тела, - её абсцисса, - ордината, - аппликата; - кратчайшие расстояния от до осей соответственно .

По определению:

28.1

Рисунок 28.2

-

- осевые моменты инерции тела относительно осей соответственно ;

28.2

-

- центробежные моменты инерции тела относительно осей соответственно ; обращаем внимание на принятую условность в терминологии - «относительно» той оси (из числа 3-х - ), которая оказывается отсутствующей в обозначении центробежного момента; например - это центробежный момент инерции тела относительно оси .

Пусть - масса тела ; и - расстояния до оси ближайшей и наиболее удалённой частиц этого тела. Тогда, в соответствии с известной из курса высшей математики теоремой о среднем, можно записать:

28.3

где

величину называют радиусом инерции тела относительно оси .

229

Аналогичны понятия радиусов инерции тела относительно осей и -

, .

Замечания: 1. Осевые моменты инерции – арифметические величины, центробежные - алгебраические; 2. Больше приходится иметь дело с осевыми моментами инерции и для сокращения речи слово «осевой» часто опускают; во избежание путаницы, когда речь идёт о центробежных моментах инерции, сокращение в термине недопустимо.

28.4. Примеры на использование общих формул

для определения моментов инерции тел

Стержень - это прямолинейно-протяжённое однородное твёрдое тело постоянного поперечного сечения. Как математическая модель стержень – это отрезок прямой, у которого одинаковые элементы длины имеют одинаковые веса.

28.4

Ось, проходящую через центр тяжести тела, называют центральной.

Считая известными массу ( ) и длину ( ) вывести формулу для вычисления момента инерции стержня относительно перпендикулярной ему центральной оси.

П

К выводу формулы для вычисления момента инерции стержня

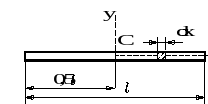редставляем стержень в виде бесконечно большого числа бесконечно тонких дисков, нанизанных на ось . Один из них, толщиной , изображаем (см. рис.3).

Если руководствоваться обозначениями, использованными на рис.3, то необходимо определить .

О

Рисунок 28.3

сновное значение имеют удалённые от оси частицы, но для них . Поэтому общая формула 1 в рассматриваемом случае принимает вид:

.

Т.к. , где - площадь поперечного сечения стержня; - объём выделенного элемента, а - плотность материала, то:

230

- это объём стержня; - его масса. Поэтому:

28.5

28.6б

- формула для вычисления момента инерции однородного прямолинейного стержня относительно центральной, перпендикулярной ему оси.

Цилиндр (однородный полый – как общий случай; сплошной однородный– как частный случай от общего, но в подавляющем большинстве встречающийся в расчётной практике; диск - сплошной однородный цилиндр малой длины).

З ная массу , внутренний и наружный радиусы однородного полого цилиндра, определить его момент инерции относительно продольной оси симметрии. Если руководствоваться изображениями на рис.4, то определить момент инерции относительно оси -

П

К выводу формулы для вычисления момента инерции цилиндра

Рисунок 28.4

28.7

редставляем цилиндр состоящим из бесконечно большого числа бесконечно тонких (толщиной ), вставленных друг в друга полых цилиндров. - радиус произвольного из них. Тогда, начиная с 28.1, получаем:

.

Выражение, заключённое в квадратных скобках, - это площадь поперечного сечения полого цилиндра. Она умножается на длину цилиндра; поэтому в фигурных скобках записана формула для вычисления объёма полого цилиндра. Т.к. объём полого цилиндра умножается ещё и на плотность материала, то окончательно получаем:

28.6а

- формула для вычисления момента инерции однородного полого цилиндра относительно его продольной оси симметрии.

231

Для диска и сплошного цилиндра и, поэтому:

- формула для вычисления момента инерции однородного диска (и сплошного цилиндра) относительно централь-ной оси, расположенной перпендикулярно торцам.

Задание студентам.- Если разделить 28.6а на 28.6б, то получится

.

Можно ли из этого сделать вывод, что при одинаковых длинах и наружных радиусах сплошного и полого цилиндров момент инерции относительно продольной оси будет большим у полого цилиндра? Подискутируйте с коллегами и установите истину.

Шар, конус. Двух рассмотренных примеров достаточно было для уяснения применявшегося «прямого метода» получения формул для вычисления осевых моментов инерции тел. Поэтому сообщаем лишь результаты:

м омент инерции однородного шара относительно центральной его оси - ; момент инерции однородного конуса относительно его оси симметрии - .

Замечание: с целью облегчения запоминания обращаем внимание, что выражения для и отличаются лишь коэффициентами, которые соотносятся как числа Пифагора - .

Диск, центральная ось параллельна торцам

Обозначения осей сохраняем прежними (см. рис.4): центральная ось, перпендикулярная торцам диска; и - центральные взаимно перпендикулярные оси, расположенные в средней плоскости между торцами диска.

В соответствии с общими формулами 28.1

.

Применительно к диску в записанных интегралах (суммах) подавляющее значение имеют удалённые частицы, а для них , , т.е. в рассматриваемых интегралах доля инженерно ничтожна и поэтому

232

28.8

.

Учитывая очевидное равенство и результат 28.6б получаем:

.

28.5. Формула, связывающая моменты инерции тел относительно параллельных осей

Н

К выводу формулы, связыва-ющей моменты инерции отно-сительно параллельных осей

Рисунок 28.5

а рис.28.5: С – центр тяжести тела массой ; - центральная ось с известным моментом инерции . - ось, параллельная и проходящая от неё на расстоянии . Вывести формулу для вычисления момента инерции относительно оси . - масса элементарной частицы рассматриваемого тела (точка М). - начинающаяся в центре тяжести С ось, расположенная перпендикулярно и пересекающая (в точке А) ось . Из М опускаем перпендикуляры на

(точка D) и (точка В). Обозначаем MD , MB .

В соответствии с дававшимся понятием . По теореме косинусов: . Но - равно координате точки М по оси . Таким образом:

Характеристики

Список файлов книги