ztm15 (850189), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

периода колебаний

Расчёты на устойчивость движения автомобилей по дорогам требуют знания их моментов инерции. Один из возможных путей такого определения представлен на рис.10:

Рисунок 29.10

.

З

К определению момента инерции шатуна

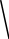
a

C

аписанные формулы являются прямыми следствиями результата 29.10. К моментам инерции относительно центральных осей автомобиля можно перейти с помощью математической связи между моментами инерции относительно параллельных осей, что рассмотрено в подразделе 28.5. Вопросы же определения положений центров тяжести рассматривались в статике.

П

Рисунок 29.11

ервая из записанных двух формул может быть использована и для определения момента инерции шатуна (см. рис.29.11) – деталь двигателя внутреннего сгорания (имеются практически в любом автомобиле, тракторе, тягаче и мотоцикле).

29.10.2. Нахождение моментов инерции тел cпособом маятника сравнения

Тело, момент инерции которого необходимо определить, превращают (см. рис.10 и 11) в физический маятник. Через ось подвеса перебрасывают нить с грузиком (например гайкой) на конце – это математический маятник в реальном исполнении. Длина математического маятника экспериментально подбирается такой, чтобы его колебания оказались синхронными колебаниям физического маятника. Тогда момент инерции тела относительно точки подвеса можно определять по формуле 29.12 - .

254

2

К определению моментов инерции тел способом крутильных колебаний

9.10.3. Нахождение моментов инерции тел cпособом крутильных колебаний

С хема устройства для нахождения моментов инерции тел способом крутильных колебаний изображена на рис.29.12: главный вид и под ним - вид сверху; - длина стальной проволоки, верхний её конец неподвижен, ось проходит через центр тяжести диска, нижний конец жёстко соединён с центром диска. - радиальная метка на диске; - неподвижная горизонталь, с которой совпадает метка в положении статического равновесия системы «проволока-диск»; - текущий угол закрученности проволоки; - момент, приложенный к диску со стороны проволоки.

При небольших углах закручивания (15-30^о, что практически всегда достижимо и зависит от длины )

,

где .

К

Рисунок 29.12

рутильная жёсткость проволоки определяется экспериментально, либо подсчитывается по известной из курса сопротивления материалов формуле.

На основании 29.7 записываем дифференциальное уравнение вращательного движения диска:

, где - экспериментально определяемый период колебаний системы «проволока-диск».

Практически более приемлема конструкция, в которой к нижнему концу проволоки жёстко прикреплён патрон от токарного станка, а уже в него закрепляется деталь с искомым моментом инерции.

Задание: вывести формулу, по которой можно определять момент инерции детали, закрепляемой в патрон от токарного станка.

255

29.11. Закон об изменении кинетического момента в центромассовой системе отсчёта

Центромассовая система отсчёта – это система отсчёта, поступательно перемещающаяся относительно инерциальной системы и начало которой во времени совпадает с центром масс механической системы.

В

29.14

центромассовой системе отсчёта закон об изменении кинетического момента имеет ту же математическую форму, что и в инерциальной системе - , где

- центр масс любой, конкретно рассматриваемой механической системы;

15

- главный момент внешних сил относительно центра (который в общем случае перемещается относительно инерциальной системы с переменным ускорением);

- кинетический момент, определяемый по скоростям частиц относительно центромассовой системы отсчёта;

Результат 29.14 теоретически предсказывается теми же, многократно применявшимися, методами векторной алгебры. Вот этот преобразовательный процесс.-

.

В получившемся выражении первая сумма равна нулю - векторно перемножаются сонаправленные векторы. Во второй сумме добавляются, в отличие от преобразовательного процесса рассмотренного в подразделе 7.4, переносная и кориолисова силы инерции (т.к. центромассовая система не является инерциальной) -

.

Но т.к. центромассовая система – это система перемещающаяся поступательно относительно инерциальной, то кориолисовы силы инерции для всех точек системы равны нулю. Равным нулю оказывается и главный момент от переносных сил инерции. И действительно:

.

Результат 29.14 распространить на произвольные системы отсчёта

нельзя. Объясните - почему?

256

29.12. Дифференциальные уравнения плоского движения твёрдого тела и примеры их применения

Н

К динамике плоского движения

а рис.29.13 изображена плоская фигура, - центр её тяжести, - масса, - метка для отсчёта угловой координаты ; - инерциальная, - центромассовая системы отсчёта.

Объединяя опорные факты подразделов 25.1 и 29.7, получаем:

29.15

,

,

Рисунок 29.13

.

- дифференциальные уравнения плоско движущегося тела.

П

К качению кольца по наклонной плоскости

РИМЕР 29.5.- Качение кольца по наклоной плоскости

Д ано. – Кольцо массой и радиусом скатывается по наклонной плоскости, характеризуемой углом (см. рис.29.14). Коэффициент трения скольжения кольца по наклонной плоскости - .

Требуется. - Область возможных значений угла (от 0 до 90^о) разбить на две – область чистого качения и область качения с проскальзыванием.

Р

Рисунок 29.14

ешение.- Принимаем к рассмотрению кольцо. Внешними для него силами являются: сила тяжести , нормальная

и касательная составляющие реакции плоскости ( - сила сцепления – при отсутствии проскальзывания, либо - при наличии проскальзывания).

Рассматриваем случай отсутствия проскальзывания. Тогда точка соприкосновения кольца с плоскостью является мгновенным центром скоростей и, как известно из кинематики, имеет место равенство:

а

.

257

Теперь (а) дополняем тремя дифференциальными уравнениями 29.15 и, после совместного их решения, отвечаем на поставленный в задаче вопрос.-

ба

ва

г

.

Из (а) и (г):

д

.

Из (в) и (д):

еа

.

Условие отсутствия проскальзывания (из статики) имеет вид: , т.е. учитывая (е) получаем: . Откуда

условие отсутствия проскальзывания кольца по наклонной плоскости принимает вид: . Для кольца: . Поэтому в данной задаче условие отсутствия проскальзывания принимает вид:

.

Задание для самостоятельной работы: измените в условиях решённой задачи лишь одно – катится не кольцо, а сплошной однородный диск. До какого значения угла будет отсутствовать проскальзывание диска по наклонной плоскости?

258

П

Стержень за концы подвешен на двух нитях

РИМЕР 29.6.- Стержень подвешен за два конца. Одна нить перерезается

Д ано. – Однородный стержень за концы А и В подвешен к потолку на двух нитях (см. рис.29.15). Одна из них (правая) перерезается.

Т

Рисунок 29.15

ребуется. - Найти натяжение левой нити на бесконечно малом промежутке времени, следующим сразу же за моментом перерезания правой нити.

Решение.- Принимаем к рассмотрению стержень. Внешними, действующими на

него силами, являются натяжение левой нити и сила тяжести стержня.

Из получаем: .

Из .

Из геометрии: . При малых : .

В

29.16

связи с этим, второе из составленных дифференциальных уравнений принимает вид: . Подставляем полученное в первое уравнение:

29.17

. Учитываем, что и получаем: .

П

Падение диска с разматыванием нити

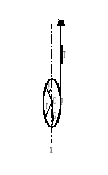РИМЕР 29.7.- Падение диска с разматыванием навёрнутой на него нити, свободный конец которой прикреплён к потолку

Дано. – На рис.29.16 изображён сплошной однородный диск с намотанной на него нитью, свободный конец которой прикреплён к потолку. - вес диска, - радиус; - натяжение нити.

Требуется. - Определить натяжение нити.

Р

29.18

ешение.- Принимаем к рассмотрению диск с прилегающим к его жолобу небольшим вертикальным участком нити (см. рисунок).

Т

Рисунок 29.16

раекторией центра тяжести диска является вертикальная прямая - это видно из .

259

- мгновенный центр скоростей для диска .

Из : . Подставляем это в последнее выражение предыдущей строки и получаем: .

Характеристики

Список файлов книги