ztm15 (850189), страница 3
Текст из файла (страница 3)
Из 
: 
.
Объединяем уравнения двух последних строк, учитываем, что 
и находим: 
.
29.13. Начальные сведения о динамике произвольно и сферически движущихся тел
29.13.1. Уравнения, исторические сведения
Для математического описания произвольно движущегося тела относительно инерциальной системы отсчёта по аналогии с предыдущим подразделом можно ввести центромассовую систему отсчёта. Тогда:
-
уравнения, описывающие движение центра тяжести тела относительно инерциальной системы отсчёта 
;
-
уравнения, описывающие сферическое движение тела в центромассовой системе отсчёта.
Но ... в отличие от динамики плоского движения, здесь имеются серьёзные трудности – проблемы возникают при разворачивании 
(
).
Далее будем иметь ввиду сферического движение. Для него можно получить уравнения (см. следующий пункт – 29.13.2):
.
260
Их называют приведенными к форме Коши «динамическими уравнениями Эйлера» (или «уравнениями Эйлера-Пуассона», или «уравнениями Даламбера-Эйлера»). В них 
связаны с телом, причём являются главными его осями инерции.
У читателя должен возникнуть естественный вопрос: «Но где в уравнениях 29.18 координаты, которыми определяется положение тела относительно базовой системы отсчёта (инерциальной, или центромассовой»)?
Полная система дифференциальных уравнений сферического движения твёрдого тела получится тогда, когда к тройке уравнений 29.18 добавить ещё и
к
инематические уравнения Эйлера в форме Коши: 
29.19
(см., например, «Лунц Я.Л. Введение в теорию гироскопов.- М.: Наука, 1972.- 296с.»). При этом, напоминаем: 
- углы Эйлера (
- собственного вращения, 
- прецессии, 
- нутации).
Естественно желание систему дифференциальных уравнений 29.18-19 решить чисто аналитически, да ещё для общего случая.
Этого до сих пор не удалось сделать. Аналитические решения известны лишь для частных случаев: Леонард Эйлер (в 1759 г. - 
); Жозеф Луи Лагранж (1815 г. - 
): Софья Ковалевская (1888 г. - 
, а центр тяжести расположен в экваториальной плоскости эллипсоида инерции) и некоторые другие.
Насколько важны и трудны были аналитические решения свидетельствует исторический факт с С.Ковалевской (1850-1891).- Французская академия наук трижды объявляла конкурс на лучшую работу по динамике сферического движения. Лишь на третий раз поступила стоящая работа (без фамилий – под девизами). Настолько стоящая работа, что жюри решило премию с 3000 франков увеличить до 5000.
В настоящее время уравнения 29.18-19 и компьютерная техника позволяют любой конкретно-числовой случай сферического движения решать и анализировать численным методом. Принципиальный подход к этому был дан в подразделе 3.6.
261
29.13.2*. Вывод дифференциальных уравнений 29.18
Н
К выводу уравнений 18
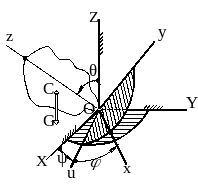а рис.29.17: 
- инерциальная система отсчёта; 
- главные оси инерции твёрдого тела; 
- его центр тяжести, 
- вес. 
- линия узлов; - углы Эйлера ( - собствен-ного вращения, 
- прецессии, - нутации).Как и для вращательно движущегося тела (см. подраздел 7.3) получаем:
а
.Н
Рисунок 29.17
а этом аналогия с вращательно движущимся телом заканчивается, ибо следует учитывать переменность вектораугловой скорости и равенства нулю центробежных моментов инерции относительно осей .
Т.к. 
, 
,
т
б
о второй интеграл выражения (а) принимает вид:
.
В полученном выражении отсутствуют центробежные моменты по той причине, что оси главные.
Подставляем (б) в (а) и учитываем, что 
. Получаем:
в
.Переходим к взятию производной по времени от последнего выражения. При этом, учитываем переменность не только 3-х проекций угловой скорости, но и ортов 
. Используем также известные из кинематики формулы:
.
Поскольку дальше идёт недлительная процедура с повторением неоднократно ранее встречавшихся методов, предоставляем обучающемуся возможность самостоятельно провести соответствующие алгебраические преобразования и получить дифференциальные уравнения 29.18.
262
2 Волчок
9.14*. О гироскопе с тремя степенями свободы, прецессионном движении и условии неподвижности его оси вращения
Г
Рисунок 29.18
29.20
ироскоп – это тело, быстро вращающееся относительно своей оси симметрии. С древних времён привлекал к себе внимание устойчивостью оси вращения гироскоп в форме волчка (юлы) – см. рис.18, где 
– маховик, 
– физическая ось волчка, 
– его керн (наконечник), 
– опора; 
- математическая ось волчка, 
- изображение наконечника в большом масштабе; 
– центр сферического движения (точка соприкосновения опоры с керном); 
– конец (торец) оси ; 
- наклон оси к вертикали; 
- центр тяжести волчка, 
- его вес; 
- отклонение центра тяжести от центра сферического движения; 
- угло- вая скорость волчка вокруг оси (большая угловая скорость); 
- угловая скорость математической оси волчка в её сферическом движении относительно опоры (малая угловая скорость волчка).
В
Гироскоп в двойном кардановом подвесе
Рисунок 29.19
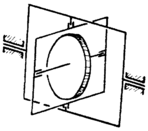15-19 веках мировое сообщество крайне интересовало открытие и освоение новых земель. Это, и вопросы безопасности мореплавания, настоятельно требовали приборов для ориентирования. По этим причинам и было обращено внимание на свойство волчка неизменным сохранять положение математической оси относительно звёзд. Вначале пытались использовать для создания навигационных приборов непосредственно волчки (англичанин Серсон и др.), но в практику вошла другая конструкция - гироскоп в двойном кардановом подвесе – см. рис.29.19. Основное свойство гироскопа с 3-мя степенями свободы (неизменным сохранять положение математической оси в инерциальной системе отсчёта) позволило ему получить широкое практическое использование в качестве приборов–указателей направления (гирокомпасы, гирогоризонтали, гировертикали и т.п.), что используется в авиации и на кораблях, в торпедах и ракетах, в шахтных геодезических приборах и для обеспечения заданных траекторий скважин (которые бурят на глубины до десятка километров).
263
Но есть «враг» основному свойству гироскопа - это прецессия его математической оси – изменение со временем положения оси в инерциальной системе отсчёта: французскому физику Фуко (а термин «гироскоп» считается ввёл он - в 1852 г.) удавалось добиваться угловой скорости прецессии (
) из расчёта 1 оборот за сутки. К 70-м годам 20 столетия эту угловую скорость удалось понизить до 2-3-х угловых секунд за 24 часа.
Описанные свойства гироскопа с тремя степенями свободы не есть нечто необъяснимое – они вытекают из методов и опорных фактов теоретической механики.
О
ва
сложности точного анализа гироскопических явлений уже сказано - в предыдущем подразделе - и при появлении у будущего инженера необходимости изучить тонкости этого важнейшего научно-технического достижения мы рекомендуем обратиться к уже упомянутой книге Я.Л. Лунца.Здесь же обучающегося ознакомим c менее точным, но зато с существенно более простым подходом к количественному анализу гироскопических явлений.
Д
опущение: если у гироскопа большая угловая скорость ( ) на пару и более порядков превышает малую ( ), то его кинетический момент можно определять по формуле:
(как для тела вращающегося вокруг неподвижной оси, совпадающей с главной осью инерции этого тела).
Исходя из принятого допущения выведем формулу для вычисления малой угловой скорости гироскопа. При этом, будем руководствоваться изображениями на рис.29.18.
С
22
целью удобства геометрического представления вектор
через масштабный коэффициент 
представляем в виде направленного отрезка 
(подобное уже делалось - в подразделе 22.7 - при рассмотрении эллипсоида инерции). Причём, масштабный коэффициент подбираем таким, чтобы начинался в точке 
и заканчивался в 
, т.е. вводим соотношение 
а
.
Скорость конца вектора (точки ), как известно из сферического движения, 
, или, с учётом (а), 
.
264
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
