ztm14 (850188), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

29.3. Формула для вычисления кинетического момента вращательно движущегося тела

Н

К выводу формулы для вычисления кинетического момента вращающегося тела

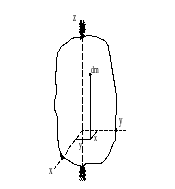а рис.29.3: - угловая скорость тела; - её проекции на оси связанной с телом системы . - масса отдельной частицы; - её радиус-вектор, , - координаты.

Т.к. , , то, пользуясь правилом представления двойного векторного произведения разностью

д

29.5

вух векторов,

,

получаем:

Рисунок 29.3

.

Т.к.

, ,

то

.

Итак, с учётом понятий о моментах инерции, получаем:

к

29.4

инетический момент вращательно движущегося тела определяется выражением

.

29.4. Закон об изменении кинетического момента

Берём производную по времени от кинетического момента произвольной механической системы. При этом, применяем правило «производная от суммы равна сумме производных» и другие, ранее уже встречавшиеся:

.

245

В получившемся выражении первая сумма равна нулю (т.к. векторно перемножаются сонаправленные векторы - ).

Движение рассматривается в инерциальной системе отсчёта. Поэтому:

, где

и - равнодействующие внешних и внутренних сил, действующих на - тую частицу.

С учётом свойства внутренних сил , получаем:

-

производная по времени от кинетического момента относительно произвольного центра инерциальной системы отсчёта для любой механической системы равна главному моменту относительно того же центра всех внешних, действующих на систему сил.

29.5. Закон сохранения кинетического момента

В проекциях на оси координат математическое выражение закона об изменении кинетического момента приобретает вид:

; ; .

Если , или , либо , либо ),

то , либо ( - это , или , или ).

Приводим пример на закон сохранения кинетического момента. По причине большой исторической значимости отводим ему подраздел.

29.6. Закон площадей Кеплера

Н

Рисунок 29.4

К закону площадей Кеплера

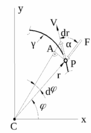а рис.4: – центр масс планеты (как материальная точка), - его траектория, - скорость, - радиус-вектор; - угол между векторами и ; - действующая на планету со стороны притягивающего центра (Солнца) гравитационная сила; Гелиоцентрическая система отсчёта, взятая так, чтобы в начальный момент

246

времени векторы и располагались в плоскости ; - полярный угол (определяет положение радиус-вектора относительно полярной оси ).

Понятно, что траектория точки расположена в плоскости ( ).

Т.к. - центральная сила (всё время проходит через точку ), то:

. Откуда:

анетический момент вращательно движущегося тела определяется

.

За время радиус-вектор получит приращение и ометёт площадь , равную площади треугольника :

.

Подставляем полученное выражение в (а) и получаем:

29.6

- за равные промежутки времени радиус-вектор ометает равные площади. Это и есть 2-й закон Кеплера (закон о площадях).

Два других закона Иоганна Кеплера (1571-1630):

первый – планеты движутся по эллипсам и в одном из фокусов каждого такого эллипса находится Солнце (уравнения траекторий планет и космических аппаратов см. в подразделе 11.7);

третий - времена обращений планет относятся между собою как полуторные степени средних их расстояний до Солнца.

З

29.7

аконы Кеплера явились солидным экспериментальным фундаментом к теории ещё для Ньютона - при написании им «Математических начал», т.е. рассмотренный пример в очередной раз подтвердил целесообразность обучающемуся воспитать в себе высокое доверие к механическим явлениям, которые он в своей инженерно-практической деятельности будет предсказывать, используя методы и опорные факты теоретической механики.

29.7. Математическое выражение производной по времени от кинетического момента вращательно движущегося тела. Основное уравнение динамики вращательного движения

В подразделе 29.3 показано, что кинетический момент вращательно движущегося тела определяется формулой:

.

Используя известное из математики правило взятия производной от произ-

ведения двух переменных, получаем:

247

.

В рассматриваемом случае .

- правая декартова система координат. Это значит:

.

Тогда, учитывая известные из кинематики связи и ,

получаем:

.

Таким образом:

.

После приведения подобных членов получаем

м атематическое выражение производной по времени от кинетического момента вращательно движущегося тела:

.

К первым двум составляющим математического выражения 6 возврат будет при рассмотрении динамических нагрузок на опоры вращательно движущегося тела (в разделе «Метод кинетостатики»).

В данном же разделе внимание уделим лишь проекции математического выражения 29.6 на ось , которую, по причине сходства с , называют

о сновное уравнение динамики вращательно движущегося тела –

.

2

Скамья Жуковского

9.8. Рядовые примеры на применение закона об изменении кинетического момента

П РИМЕР 29.1.- Скамья Жуковского

Д

Рисунок 29.5

ано. – На рис.29.5 изображён человек с гантелями в руках в двух положениях: в первом - руки широко расставлены и момент инерции системы относительно оси вращения кгм², угловая скорость об/с; во втором положе-

248

Характеристики

Список файлов книги