ztm1 (850175), страница 7
Текст из файла (страница 7)
В соответствии с 12.8, 12.12 и правилами векторного произведения имеем:
Откуда:
12.13а
На первый взгляд кажется, что формулы 12.13а сложны для запоминания.
Процесс написания любой из трёх формул 12.13а оказывается простым, если его раскладывать на 3 этапа:
1. По исходной векторной формуле 
(которую надо, конечно, помнить) пишется скалярная формула 
;
33
2
К способу перестановки индексов
. К буквам последней записанной формулы приписываются индексы в представленной на рис.9 последовательности их появления при движении вдоль круга (x-y-z, либо y-z-x, либо z-x-y);3. Вторые произведения в правых частях (стоящие после минусов) получаются из первых - путём написания тех же букв и индексов, но индексы при их привязке к буквам меняют местами.
С
Рисунок 12.9
пособ перестановки индексов используется также в кинематике (
),многократно в динамике и поэтому им целесообразно владеть свободно. Что значит «свободно»? Это значит любую из трёх формул 13а по команде товарища следует успевать записывать за 10 секунд.
Обычно стремятся к более простым записям. По этой причине вместо двухбуквенных обозначений 
; 
пишут однобуквенные -
и 
. В этом случае формулы 13а принимают вид:
12.13б
12.12. Понятие о главном моменте. Аналитический способ его вычисления
С математической точки зрения рассматриваемое понятие тождественно изложенному в подразделе 8 (где рассматривалось понятие «главный вектор»).
Пусть имеем систему из 
сил - 
. и пусть 
- радиус-векторы, определяющие положение точек приложения этих сил в произвольной правой системе координат.
Величину 
, определяемую из выражения
1
2.14 
называют «главным моментом заданной системы сил относительно центра О».
Величины 
, подчинённые условию
1
2.15 
,
34
называют «главными моментами заданной системы сил относительно осей соответственно ».
Из 12.8, 12.12, 12.14 и 12.15 видим, что
1 2.16 
, где
- моменты сил заданной системы (
) относительно осей соответственно 
.
ПРИМЕР 12.2. - На вычисление главного момента (аналитическим методом)
Дано: проекции сил 
и координаты точек их приложения определяются из приводимой таблицы
| X, н | Y, н | Z, н | x, м | y, м | z, м |
| 0 | 100 | -60 | 1,0 | 0,0 | 0,0 |
| 100 | 80 | 0 | 0,8 | -0,5 | 0,0 |
| 50 | 0 | 80 | 0,5 | 0,6 | 1,0 |
| -40 | 0 | 0 | 0,4 | 0,0 | -0,8 |
Требуется: определить главный момент заданной системы сил относительно начала координат (который обозначим точкой О).
Решение.
Нм.
Аналогично
35
Нм.
Нм.
Итак, главный момент заданной системы сил:
Его модуль:
Нм.
Направляющие косинусы главного момента:
.
1
К выводу зависимости 12.17
2.13. Зависимость между главными моментами относительно различных центров Э
та зависимость определяется правилами векторной алгебры. На рис.10: О – некий базовый центр (например – начало системы 
); А – произвольно взятый другой (новый) центр.
В
Рисунок 12.10
соответствии с правилами векторной алгебры и ранее принятыми понятиями для произвольной системы сил
получаем:
Итак:
36
-
г
12.17
лавный момент произвольной системы сил относительно любого центра А больше главного момента этой же системы относительно ранее взятого центра О на величину, равную векторному произведению радиус-вектора, проведенного из нового центра в старый, на главный вектор. Следствие: у
12.18
системы сил с нулевым главным вектором главный момент не зависит от положения центра (относительно которого он вычисляется).В
Рисунок 12.12
Рисунок 12.13
математических записях рассмотренного подраздела пределы суммирования (от
=1 до =n) при символах 
опускались. С целью сокращения записей это часто при изложении курса будет делаться и в дальнейшем.12.14. Понятия о противоположных силах, паре сил и её моменте, о силовом винте
Д
12.19
ве силы называют противоположными, если они расположены на одной прямой (говорят – «на одной линии действия»), направлены в разные стороны и равны по модулям. П
12.20
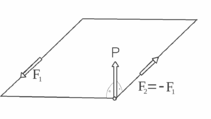
ара сил (кратко: пара) – это совокупность двух противоположно направленных сил, линии действия которых не совпадают (см. рис.11).
К понятиям «пара» и «вектор-момент пары»
Плечо пары (h) – это кратчайшее расстояние между линиями действия сил.
В
Рисунок 12.11
ектор-момент пары сил (кратко: момент пары) - это свободный вектор с модулем равным произведению модуля силы на плечо пары (
) и который перпендикулярен плоскости действия пары, причём направлен так, чтобы глядя ему навстречу можно было видеть пару сил стремящейся повернуть тело (к которому она приложена) против хода часовой стрелки. С
12.21
иловой винт (кратко –«винт»; иногда называют «динамическим винтом») - это совокупность трёх сил (рис.12.12 и 12.13), две из которых образуют пару, а третья перпендикулярна плоскости её действия.37
К понятию «силовой винт»
Представление силового винта двумя векторами
Называют:
момент винта - это момент, создаваемый парой сил винта;
сила винта - это сила, расположенная перпендикулярно плоскости действия пары силового винта;
ось силового винта - это линия действия силы винта –
(кратко: ось винта).
38
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
