ztm6 (850180), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

зываний, т.е. обеспечивая равенство нулю скоростей точек ; - центр поворота – точка пространства, оказывающаяся (при движении автомобиля по рассматриваемому закруглению) центром сферического движения и 1-го, и 3-го колёс; и - их мгновенные оси вращения, и - угловые скорости.

Если бы колёса 1 и 3 были закреплены на одной оси, то покрышки на поворотах катились бы по дороге с проскальзываниями и быстро изнашивались.

119

Формула 18.19 и проведенный её анализ позволяют дать следующую рекомендацию по определению скоростей точек сферически движущегося тела:

с

18.21

корости точек сферически движущегося тела в любой момент времени распределены как при вращательном движении, осью которого является мгновенная ось, а угловая скорость равна угловой скорости сферического движения;

пример применения результата 18.21 см. в примере 18.6.

18.3.3. Ускорения точек сферически движущегося тела

. Итак, получена

в

18.22

екторная формула, выражающая ускорения точек сферически движущегося тела через угловые скорость и ускорение ( ):

.

Несмотря на то, что получена точно такая же формула, как и для вращательного движения, отличия имеются. И существенные. Рассмотрим их.

При вращательном движении тела вокруг оси вектор всё время расположен на оси вращения (если условиться его начинать из какой-либо точки этой оси), т.е. его годограф, и поэтому угловое ускорение, также расположены на

о

При сферическом движенеии не

си вращения ( ). При сферическом же движении вектор угловой скорости переменен, прежде всего по направлению. Поэтому

в

18.23а

ектор углового ускорения (как касательная к годографу ) при сферическом движении расположен, как фунция времени, под углом по отношению к вектору угловой скорости - см.рис.18.18.

С

Рисунок 18.18

математической точки зрения связи и идентичны, а стремление новые знания сводить к известным, приводят к формулировке:

в

18.23б

ектор углового ускорения равен скорости конца вектора угловой скорости, при условии, что его начало (на рис.18.18 - полюс) неподвижно.

Часто вектор угловой скорости сферически движущегося тела постоянен по модулю и вращается вокруг неподвижной оси (описывает поверхность прямого

120

к

Вычисление . Случай 18. 23в

ругового конуса – см. ниже пример 6). В этом случае вектор можно уподобить стержню (см. рис.18.19), вращающемуся вокруг неподвижной оси с угловой скоростью и тогда, пользуясь аналогией , можно записать:

18.23в

.

М

Рисунок 18.19

Составляющие ускорения сферически движущегося тела

атематическая одинаковость формул для вычис-ления ускорений при вращательных движениях вокруг оси и точки (формулы 18.15 и 18.22), с учётом их отли-чия по содержанию, рассмотренного в 18.23 (а-б-в), поз-воляют рекомендовать трёхшаговую процедуру вычис-ления ускорения точек сферически движущегося тела:

1 . Тело предполагается в рассматриваемый момент времени вращающимся вокруг неподвижной оси, совпадающей с мгновенной осью вращения (см. рис.18.20); при таком предположении определяется нормальная составляющая ускорения – по формуле ; направлена она перпендикулярно и пересекает её; называют осестремительной составляющей ускорения;

2

18.24

. Тело предполагается вращающим-ся вокруг неподвижной оси, проходящей через центр сферического движения па-раллельно ; при таком предположении определяется касательная составляющая ускорения - модуль по формуле ; направлена же эта состав-ляющая так, чтобы глядя навстречу век-тору видеть, что уподобленный силе вектор действует в направлении поворота тела против хода стрелки часов; называют вращательной составляющей ускорения.

3

Рисунок 18.20

. Полное ускорение точки равно сумме осестремительной и вращатель-ной составляющих - .

121

П

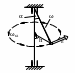
Кинематика конической шестерни, обегающей непод-вижное зубчатое колесо

РИМЕР 18.6.- На кинематику сферического движения тела

Д ано.- Водило 1 вращается (рис.18.21) вокруг неподвижной вертикальной оси с постоянной угловой скоростью ; 2 – подвижное и 3 – неподвижное конические зубчатые колёса; м; .

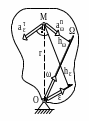
Определ. скорость и ускорение точки .

Р

Рисунок 18.21

ешение.- Тело 2 (шестерня) совершает сферическое движение вокруг центра , без скольжения обкатываясь по неподвижому зубчатому колесу 3. Следовательно , т.е. -

мгновенная ось вращения тела 2. В рассматриваемый момент времени точка движется в направлении зрачка читателя. Поэтому (в соответствии с 18.19) вектор направляем от к .

Модуль скорости точки , принадлежащей вращательно движущемуся телу 1:

.

Модуль скорости точки , принадлежащей сферически движущемуся телу 2:

.

Точки и совпадают во времени. Поэтому

.

Исходя из тех же результатов 18.19 и 18.21 находим скорость точки :

м/с

и направлена она перпендикулярно плоскости чертежа в сторону зрачка читателя.

Мгновенная ось вращения тела 2 и водило расположены (в функции времени) в одной вертикальной плоскости , что позволяет заключить:

122

исходящий из точки , постоянный по модулю вектор , вращается вокруг оси с постоянной угловой скоростью и, поэтому, траекторией его конца является окружность.

Применяя результат 18.23в, находим модуль углового ускорения:

.

Направлен вектор углового ускорения (в соответствии с результатом 18.23б) перпендикулярно плоскости чертежа в сторону зрачка читателя, что на рисунке отображено значком .

Используя результат 18.24, определяем:

1. Модуль осестремительного ускорения точки

м/с² ;

направлен этот вектор по кратчайшему расстоянию от точки к мгновенной оси вращения ;

2. Модуль вращательного ускорения точки

м/с² ;

расположен вектор в плоскости чертежа (перпендикулярно и , и ) и, в соответствии с правилом пункта 2 результата 18.24, направлен влево-вверх;

3. Полное ускорение равно геометрической сумме осестремительной и вращательной составляющих – оказалось направленным от к и по модулю равным 3000 м/с².

123

19. Сложные движения точки и тела

19.1. Понятия об абсолютном, относительном и переносном движениях, скоростях и ускорениях. Обозначения

В общем случае траектория, скорость и ускорение точки относительно различных систем отсчёта различны.

Так, для наблюдателя, находящегося на перроне железнодорожного вокзала, траекторией точки обода колеса отходящего вагона является циклоида; для пассажира траектория этой же точки оказывается окружностью.

Находящийся на эскалаторе человек покоится относительно ступенек, относительно же стен и площадок метро скорость его движения отлична от нуля.

У

К понятиям об абсо-лютном, относительном и переносном движениях

скорение стартующего космонавта относительно корабля практически равно нулю, относительно Земли в несколько раз превосходит ускорение свободного падения тела.

П усть (см. рис.19.1) - как угодно движущаяся точка относительно двух систем отсчёта. Любую из них назовём «неподвиж-ной». Определяемся конкретно – неподвижной называем первую ( ) систему; синонимы - «основная», или «базовая» система отсчёта. Как здесь, так и в дальнейшем, уславливаемся на рисунках оси неподвижной системы отсчёта выделять примыкаемыми к ним под углами 45^о короткими отрезками (штриховкой).

Т

Рисунок 19.1

огда вторую систему отсчёта ( ), произвольно движущуюся относительно системы ( ) принято называть подвижной.

Систему , начало которой совпадает с началом ( ) и которая перемещается поступательно относительно назовём «вспомогательной» системой.

Движение точки относительно неподвижной системы называют абсолютным движением, относительно подвижной – относительным.

Аналогично: «абсолютная скорость точки » (либо ускорение) – это её скорость (либо ускорение) относительно неподвижной системы отсчёта; «относительная скорость точки » (либо ускорение) – это её скорость (либо ускорение) относительно подвижной системы отсчёта.

124

Движение подвижной системы относительно неподвижной называют переносным движением. Говорят, например: «переносным движением является поступательное» (или – вращательное; или – сферическое).

Наиболее простыми получаются математические связи между абсолютными и относительными скоростями (а также ускорениями), если оперировать ещё и понятиями «переносная скорость», «переносное ускорение».

Переносная скорость точки – это абсолютная скорость той точки подвижной системы, с которой в рассматриваемый момент времени совпадает точка , т.е. если руководствоваться рис.1, то переносная скорость точки – это абсолютная скорость точки . Аналогично понятие переносного ускорения (в приведенном определении слово «скорость» надо заменить на «ускорение»).

К сведению: идея относительности движения была чужда и астрономии, и физике древних. Первым развил её Николай Коперник (1473-1543).

Рекомендуем к использованию две системы обозначений – полную (основную) и упрощённую (применяемую в простых случаях).

Полная система обозначений

При буквах, отображающих кинематические величины ( ), пишут двухсимвольные индексы - , и т.д. Первый символ - в виде буквы или буквы с цифровым индексом (М, М₂ , А, В и т.п.) - отображает точку, о скорости (или ускорении) которой ведётся речь; цифровой индекс при букве (М₂ и т.п.) удобно применять при необходимости различать между собою совпадающие точки, но принадлежащие различным телам (цифра – это номер тела). Второй символ (1, 2, 3, Р, С и т.д.) является именем системы отсчёта, относительно которой рассматривается движение (это номер тела, с которым связана система отсчёта). Если вторым символом является буква, то это означает, что система отсчёта перемещается поступательно (относительно неподвижной), а разновидность буквы (Р, С, А₄ и т.д.) является именем точки, с которой во времени совпадает начало этой поступательно перемещающейся системы отсчёта.

Характеристики

Список файлов книги