ztm12 (850186), страница 2
Текст из файла (страница 2)
Сажина Н.Б. Гравитационная разведка.- М.: Недра, 1988.- 364 с.». В ней, в частности, решаются задачи по предсказанию мест залегания полезных ископаемых и обнаружению пустот на земной поверхности. Этот вошедший в практику метод научного предсказания основан на учёте весьма малых (порядка
204
м/с2 ) отклонений в действительности имеющего место ускорения свободного падения (
) от предсказываемого теоретически (в предположении, что Гелиоцентрическая система является инерциальной).
На Земном шаре военными успешно решаются задачи по теме «стрельба по цели». К сожалению, не только на учебных полигонах, но и в боевой обстановке. В основе теорий стрельб лежит предпосылка о том, что Гелиоцентрическая система является инерциальной, а Земля вращается (вокруг оси «Северный полюс - Южный полюс») с равномерной угловой скоростью, соответствующей 1 обороту за 24 часа. Так называемая «поправка на вращение Земли» даже в артиллерии (не говоря о ракетной технике) при стрельбе из дальнобойных систем даёт величины, достигающие 150-200 метров.
Итак:
д
26.4
ля подавляющего большинства инженерных расчётов за инерциальную достаточно принимать Геоцентрическую систему. При необходимости проведения более точных расчётов, за инерциальную следует принимать Гелиоцентрическую систему. Причём, по состоянию на сегодняшний день её можно считать инерциальной системой отсчёта с любой степенью точности.26.5. Условие относительного покоя
Если центр масс механической системы покоится относительно произвольной системы отсчёта, то 
и 
(потому, что 
и ). Поэтому 1 принимает вид:
26.5
.
Если решаемая задача позволяет оперировать понятием «материальная точка», то используют более простую запись –
26.5а
26.6
,
которую называют «условием относительного покоя материальной точки».
С точки зрения изучаемых методов, условие относительного покоя – это изучавшаяся в статике векторная запись условий равновесия твёрдого тела, находящегося под действием сходящейся системы сил, с той лишь небольшой корректировкой, что ко всем внешним силам следует добавлять переносную силу инерции (оперируя с нею как с обычными силами). Скалярные эквиваленты для условия относительного покоя условимся записывать, как и в статике
205
н
К понятиям
«ускорение свободного падения»
и «сила тяжести»
о с приданием им пары индексов: «Е» - это, как и ранее, символ внешних сил; «е» - символ переносного движения.26.6. Понятия о силе тяжести и об
ускорении свободного падения
На рис.26.2 изображено:
1
– Земная ось (
- Северный и 
- Южный полюса); 2 – Земная поверхность;
3 – Экватор (Экваториальный круг, Экваториальная плоскость); 
- геомет-рический центр Земли (как шара);
4 – неподвижная нить с подвешенной на конце массой 
.
З
Рисунок 26.2
6
амечания: изобразить в одном масштабе длину нити 4 и
(расстояние между материальной точкой и центром Земли) невозможно. Как будет видно ниже очень мал и угол 
, где 
- геоцентрическая, а 
- географическая широта. Поэтому рис.26.2 - это не масштабный рисунок, а рисунок к математическому анализу.
- гравитационная сила (сила земного притяжения). По общепризнанному среди специалистов закону тяготения (в данном изложении это имеющий локальное значение закон-аксиома):
8
, где
- гравитационный параметр; 
, 
- гравитационная постоянная, 
- масса Земли; 
- расстояние от массы до центра Земли.
К сведению: гравитационный параметр 
м3/ с2 ;
если тело расположено на полюсе, то 
м; если на экваторе, то 
м*; эти числовые значения
206
рекомендованы решением 12-й Генеральной ассамблеи Международного Астрономического Союза (Гамбург, 1964 г.).
- натяжение нити.
- переносная сила инерции, приложенная к массе -
.
Т.к. угловая скорость Земли (
) во вращательном своём движении относительно Гелиоцентрической системы величина постоянная, то 
. Нормальное же ускорение
, где
- кратчайшее расстояние от массы до оси вращения (
) Земли.
Итак, расположена в одной плоскости с осью вращения , перпендикулярна к ней и направлена в сторону удаления от этой оси, а её модуль определяется формулой:
.
Условием относительного покоя тела является:
а
26.11
.В
ектор 
, определяемый из соотношения
26.7
принято называть силой тяжести тела .
26.8
Модуль 
силы тяжести 
тела называют весом этого тела.
Из 26.6 и условия относительного покоя (а) следует:
с
26.9
ила тяжести и натяжение нити образуют совокупность противоположных сил.В
26.10
еличину , определяемую из соотношения 
, называют ускорением свободного падения тела.До сих пор, говоря об ускорении свободного падения тела, мы принимали его равным примерно 9,81 м/с2. Настало время уточнить это понятие.
Проектируем векторное равенство (а) на ось, перпендикулярную натяжению нити. Получаем:
207
.
Разница между и заведомо мала. Поэтому:
, т.е.
.
Чтобы получить выражение для , проектируем векторное равенство 7 на ось 
и получаем:
.
Раскладываем 
в степенной ряд - 
Т.к. - малая величина, то 
и, поэтому:
, т.е.
.
Итак, ускорение свободного падения тела зависит от расстояния, на котором оно расположено от Центра Земли (от 
) и от географической широты .
В зависимости от всех возможных значений двух этих переменных ускорение свободного падения тел расположено в диапазоне 
м/с2.
Рекомендуем студентам самостоятельно проанализировать результат 11 и аргументировано ответить на вопрос: «почему при торгово-обменных операциях, связанных с транспортировкой дорогостоящих материалов, недопустимо количество вещества оценивать пружинными весами»?
Рекомендуем также прокомментировать утверждение (правильно оно или нет; если правильно, то почему):
26.12
«По своему существу почти в каждой решаемой задаче по статике используется условие относительного покоя 5 ».
208
26.7. Рядовые примеры, иллюстрирующие применение закона о движении центра масс в произвольной системе отсчёта
П
К условию примера 26.1
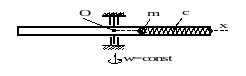РИМЕР 26.1.- Определение частоты колебаний шарика, подпружиненного внутри вращающейся трубки Д
Рисунок 26.3
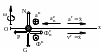
К решению примера 26. 1
Рисунок 26.4
ано. - Горизонтально расположенная трубка равномерно вращается вокруг вертикальной оси с постоянной угловой скоростью (см. рис.26.3). Внутри трубки размещена пружина, жёсткостью 
. Один конец пружины прикреплён к внутреннему торцу трубки, а к свободному её концу присоединён шарик, массой . При недеформированной пружине центр шарика расположен на оси вращения (совпадает с точкой ). Определить частоту колебаний шарика относительно трубки. Трением пренебречь.
Решение.- С продольной осью трубки связываем ось , начиная её в точке . Для шарика на рис. 4 изображаем кинематическую и силовую картину, где:
- вес шарика; 
и 
- действующие на него упругая (
) сила и реакция стенок трубки. 
и 
- скорость и ускорение центра шарика относительно трубки.
- модуль нормальной составляющей переносного ускорения центра шарика (материальной точки массой ).
- нормальная составляющая переносной силы инерции.
Касательная составляющая переносной силы инерции равна нулю - по той причине, что трубка вращается с постоянной угловой скоростью.
- кориолисово ускорение. 
- кориолисова сила инерции.
В соответствии с законом о движении центра масс относительно неинерциальной системы отсчёта (в рассматриваемом примере связана с трубкой) записываем:
.
Проектируем составленное векторное равенство на ось и получаем:
.
209
Откуда: 
, где
а
.
Итак, при 
частота колебаний шарика относительно трубки определяется зависимостью (а): при 
шарик относительно трубки, как ясно из примеров 4 и 5 предыдущего раздела, будет неподвижным - сжавшим пружину до предела, или растянув её и упёршись в противоположный внутренний торец трубки.
П
К условию примера 26.2
г
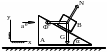РИМЕР 26.2.- Кинематическое условие, обеспечивающее неподвижность гладкого бруска относительно треугольной призмы Дано. - На треугольной призме 
расположен гладкий брусок 
(см. рис.26. 5).
О
Рисунок 26.5
пределить ускорение
, с которым необходимо перемещать треугольную призму, чтобы находящийся на ней брусок покоился.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
