l7 (1111270)
Текст из файла
Лекция 7
Формула Гаусса-Остроградского
Формула Гаусса-Остроградского является одной из наиболее важных формул в векторном анализе. Она связывает поток векторного поля через замкнутую поверхность с напряженностью векторного поля внутри замкнутой поверхности. Для векотрного поля 
:
,
причем поверхностный интеграл потока векторного поля берется по поверхности через внешнюю сторону (вектор нормали к поверхности направлен «наружу»). Правую часть формулы можно переписать в виде:
, где 
– дивергенция векторного поля 
, 
– оператор Гамильтона (набла).
Формула Гаусса-Остроградского справедлива, если выполняются два условия. Во-первых, поверхность S должна быть кусочно-гладкой, т.е. такой, что в любой ее точке можно провести касательную плоскость (поверхность задается дифференцируемыми функциями) и двусторонней (направление нормали при движении вдоль поверхности сохраняется. Во-вторых, векторное поле должно быть таким, что функции 
и их частные производные по x, y и z непрерывны в области V.
Другие варианты формулы Гаусса-Остроградского.
З
, где 
– углы, |
x y z α β γ  | которые вектор нормали составляет с осями координат. |
Кроме того, имеет место следующая формула: 
Доказательство формулы (1 вариант):
Представим векторное поле в виде суммы векторных полей: 
, где 
, найдем потоки этих векторных полей по отдельности, а затем сложим их.
Рассмотрим сначала случай поля 
. Замкнутая поверхность является цилиндроидом, ограниченным сверху и снизу поверхностями, заданными в явном виде: 
(снизу) и
| y x z D  S2 S1 z=z1(x,y)  S3 z=z2(x,y) | Координаты вектора нормали: |
| |
Так как вектор нормали направлен вниз (координата по z отрицательна), то в формуле для 
нужно выбрать знак «+». 
.
Д
D
ифференциал поверхности равен: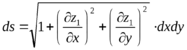
Отсюда 
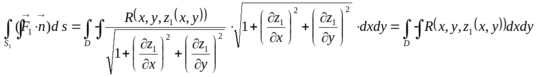Интеграл по боковой поверхности S2. Вектор нормали 
, так как нормаль параллельна плоскости xy. 
. Какая бы ни была боковая поверхность, интеграл по ней равен нулю: 
И
нтеграл по поверхности S3Рассматривается аналогично интегралу по поверхности S1 с той разницей, что вектор нормали направлен в противоположную сторону – вверх:
. Скалярное произведение 
на вектор нормали: 
, дифференциал поверхности: 
Сложим интегралы по поверхностям S1, S2 и S3:
Рассмотрим тройной интеграл по объему V:
Таким образом, для векторного поля 
формула Гаусса-Остроградского 
доказана.
Аналогично доказывается формула, если взять поле 
, и в качестве замкнутой поверхности взять цилиндроид, ось которого направлена вдоль оси y. 
(доказывается аналогично)
Аналогично и для поля 
:
Если взять поле , то – формула Гаусса-Остроградского в общем виде верна.
П
ри доказательстве мы использовали замкнутую поверхность, которая может быть представлена как цилиндроид с осью, направленной вдоль осей x, y или z. Такой поверхностью является прямоугольный параллелепипед. Если рассмотреть произвольную поверхность, то справедливость формулы не очевидна.
Разобьем произвольную поверхность на две – S1 и S2. 
Проинтегрируем векторное поле по каждой поверхности и сложим. Получатся интегралы по S1, S2 и два интеграла по сечению. Интегралы по сечению отличаются только знаком (так как векторы нормалей направлены в разные стороны), они уничтожаются при сложении. Поэтому поверхность можно разбивать на части, интегрировать по ним, результаты складывать.
П
роизведем сечение замкнутой поверхности большим числом перпендикулярных плоскостей. Формула Гаусса-Остроградского будет верна всюду, кроме границ поверхности, на границах становится справедливой при устремлении диаметра разбиения к нулю. Отсюда следует, что формула Гаусса-Остроградского справедлива для любой кусочно-гладкой поверхности.
Пример.
В качестве поля возьмем радиус-вектор: 
, S – сфера радиуса R с центром в начале координат.
Для нахождения потока вектора воспользуемся формулой Гаусса-Остроградского:
Формула Ньютона-Лейбница представляет интеграл по отрезку по значениям первообразной на границах отрезка. Формула Гаусса-Остроградского представляет собой, по существу, то же самое (вместо отрезка – объем, вместо границ отрезка – замкнутая поверхность). Эту формулу, как и формулу Грина, можно считать обобщением формулы Ньютона-Лейбница.
Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
