03_glava (1055385), страница 3
Текст из файла (страница 3)



Примеры







![]()





![]()



3.11 Домашнее задание по комбинационным устройствам.
Спроектировать комбинационное устройство цифровой электронной техники для автомата управления технологической операцией.
На вход комбинационного устройства поступают сигналы от трех датчиков. На выходе формируется выходной сигнал P=1 при десятичных кодах входных величин 0,2,3,7. При остальных кодах P=0.

Рис. 3.24
Составляем таблицу истинности.
22 21 20
| X3 | X2 | X1 | P | |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 2 |
| 0 | 1 | 1 | 1 | 3 |
| 1 | 0 | 0 | 0 | 4 |
| 1 | 0 | 1 | 0 | 5 |
| 1 | 1 | 0 | 0 | 6 |
| 1 | 1 | 1 | 1 | 7 |
Записываем логическое уравнение, связывающее входные и выходные параметры в ДНФ:








Минимизация логического уравнения с использованием карты Карно.
Проверочная таблица истинности

| X3 | X2 | X1 | P |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
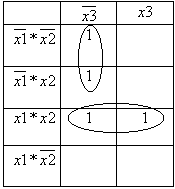


.


Построение логической схемы.
Рис. 3.25
Преобразуем уравнение по теореме Де Моргана.
(для перехода в одну логическую систему И-НЕ)
(DD1,DD2 – KI55ЛА3, И-НЕ – 2-е микросхемы). Рис. 3.26
Расчет задержки выходного сигнала P.
Входной сигнал проходит по линии, включающей в себя три последовательно соединенных логических элемента KI55ЛА3.
Проектирование печатной платы.
3.12![]() Семинар №1
Семинар №1
Задача 1.1.
Вычислить значения логических переменных Р по уравнениям для значений х1=1 и х2=0
Задача 1.2.
Изобразить логические схемы , соответствующие заданным в задаче 1.1 логическим уравнениям.

Рис. 3.28
Задача 1.3.
Для графиков функционирования автомата управления технологическим процессом, задающих логическую связь В=f(х1,х0) рис.1.3 составить таблицу истинности, записать логическое уравнение и составить логическую схему ,реализующую эту связь.
Р
ис.3.29
Задача 1.4.
Определить значение Р при значениях аргументов х1=1,х2=0,х3=1,х4=0,х5=1.
х1=1,х2=0,х3=1,х4=0,х5=1
Задача 1.5.
По графикам входных сигналов х1,х2,х3 построить графики выходных сигналов Р1 иР2.
Рис. 3.31
| Х1 | Х2 | Р1 |
| 0 1 0 1 | 0 0 1 1 | 1 1 0 1 |
Задача 1.6
Построить схемы, реализующие операции ИЛИ, И, НЕ применением элементов И-НЕ, ИЛИ-НЕ.
Рис. 3.33 Рис. 3.34 Рис 3.35
3.13 Семинар№2.Проектирование комбинационных устройств.
Задача 2.1
По заданной таблице истинности комбинационного устройства записать уравнение ДНФ, минимизировать его. По минимизированному уравнению рассчитать значения Р для всех сочетаний входных сигналов. Построить логическую схему, реализующую это комбинационное устройство.
| Х3 | Х2 | Х1 | Р |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 1 0 1 0 0 1 1 |
Неминимизированное уравнение:
Карта Карно.
Логическая схема
Задача 2.2
По заданной таблице истинности получить минимальную ДНФ. Составить логическую схему, реализующую заданную логическую связь.
| Х3 | Х2 | Х1 | Р |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 1 0 0 0 1 0 0 1 |
- неминимизированное уравнение

Рис. 3.37
Логическая схема
Задача 2.3
Минимизировать логическое уравнение:
Задача 2.4
Минимизировать логическое уравнение, представленное в карте Карно.
2.5 Комбинационное устройство имеет три входных и два выходных сигнала. Логическая связь входных и выходных сигналов задана таблицей истинности. Получить систему уравнений и минимизовать ДНФ для выходных сигналов. Построить логическую схему.
Задача 2.5
Логическую схему задачи 2.1 выполнить в базисе И-НЕ.

Рис. 3.38
Задача 2 .6
Комбинационное устройство имеет три входных и два выходных вывода. Логическая связь входных и выходных сигналов задана таблицей истинности. Получить систему уравнений в минимизированной ДНФ для выходных сигналов. Построить логическую схему применив декомпозицию.
| Х3 | Х2 | Х1 | Р1 | Р2 |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 0 1 0 1 1 1 0 | 0 0 1 1 1 1 1 0 |



























































