ЛК3 (1172679), страница 2
Текст из файла (страница 2)
Для механизма, показанного на рис. 2.1, уравнения (2.2) и (2.3) также могут иметь при одном и том же значении q1 два решения. Второму решению соответствует положение механизма АВ2С (рис. 2.5). Положение механизма АВ1С соответствует одной сборке, а положение АВ2С – другой сборке того же механизма (и, соответственно, двум решениям групповых уравнений). Способ сборки назначается следующим образом. Условно было принято, что положение группы типа ВВВ, при котором обход шарниров в последовательности А,В,С происходит против часовой стрелки, соответствует способу сборки М=1 (положение АВ2С на рис. 2.5); при обходе этих же шарниров по часовой стрелке способ сборки М=-1 (положение АВ1С на рис. 2.5). Из рисунка можно видеть, что в случае, когда АВ+ВС=ОА+ОС, существует положение, при котором возможна утрата первоначального способа сборки и переход в положение с другим способом сборки. Такое положение называют особым или сингулярным. В механизме, в котором оно существует, после прохождения особого положения возможна перемена способа сборки и, следовательно, реализация побочного решения групповых уравнений. Соответственно, механизмом реализуется не та функция положения, которая ожидается. Поэтому при проектировании механизмов следует избегать такого сочетания размеров, при котором возможно особое положение. Далее будет показано, что в особом положении у механизма проявляются и другие негативные факторы. В тех редких случаях, когда все-таки приходится проектировать механизм с особым положением, следует предусмотреть конструктивные меры, однозначно определяющие способ сборки в каждом положении механизма.

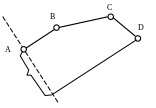
В многоподвижных механизмах два неодинаковых решения групповых уравнений, соответствующих одному и тому же значению входных обобщенных координат, могут реализовываться без разборки механизма. Например, на рис. 2.6 изображена трехподвижная платформа, в которой одному и тому же значению координат q1, q2 и q3 соответствует две разные конфигурации группы АВСD: АВ1С1D и АВ2С2D. Из рисунка нетрудно видеть, что для перехода из одной конфигурации в другую не требуется разбирать механизм; достаточно несколько раздвинуть шарниры А и D, варьируя координаты q1 и q2. Это означает, что выбор правильного решения и отбрасывание побочного нельзя осуществить простым заданием способа сборки. Каким же образом можно решить данную проблему при автоматизированном решении групповых уравнений на ЭВМ?
Возможное решение указанной проблемы рассмотрим на следующем примере. Пусть одно решение групповых уравнений (2.5) механизма, показанного на рис. 2.2, каким-то образом уже получено. Координаты, соответствующие этому положению, обозначим знаком (*): q1=q1*, q2=q2*, q3=q3*, 2=2*, 3=3*. Дадим малые приращения входных координат q1, q2, q3. Получим новые значения входных координат: q1=q1*+q1, q2=q2*+q2, q3=q3*+q3. Новому положению механизма соответствуют новые значения выходных координат: 2=2*+2, 3=3*+3. Потребуем, чтобы новое положение было близким к исходному, т.е. чтобы 2 и 3 были малыми величинами. Тогда решение 2 и 3 будет единственным, поскольку второе положение механизма, соответствующее тем же приращениям координат q1, q2 и q3, окажется далеким от исходного положения механизма.
О
пределим малые приращения 2 и 3 из уравнений (2.5) и (2.6). При этом предположим, что приращения хА, уА, хD, уD уже получены решением групповых уравнений групп I и II. Уравнение (2.5) может быть записано в следующей обобщенной форме:
При этом
Мы ищем решение ![]() векторного уравнения
векторного уравнения
где ![]() и q2 – заданные малые приращения, а
и q2 – заданные малые приращения, а ![]()
![]() удовлетворяют уравнению (2.11). Для определения
удовлетворяют уравнению (2.11). Для определения ![]() можно использовать, по предложению проф. М.З. Коловского, рекуррентную вычислительную процедуру, известную как метод Ньютона или метод касательных. В соответствии с этим методом (k+1) –е приближение для
можно использовать, по предложению проф. М.З. Коловского, рекуррентную вычислительную процедуру, известную как метод Ньютона или метод касательных. В соответствии с этим методом (k+1) –е приближение для ![]() связывается с k-м при приближенным соотношением
связывается с k-м при приближенным соотношением
Доказано, что в достаточно малой окрестности исходного решения ![]() последовательность (2.14) сходится, причем обеспечивается квадратичная сходимость. Выражение
последовательность (2.14) сходится, причем обеспечивается квадратичная сходимость. Выражение
представляет собой матрицу Якоби для системы (2.11), имеющую в рассматриваемом случае следующий вид:
Определитель этой матрицы (якобиан) определяется выражением
Выражение, стоящее в квадратных скобках, имеет простой геометрический смысл: оно представляет собой проекцию ломаной ВСD на направление, перпендикулярное звену АВ. Можно показать также, что в двух положениях механизма, соответствующих одним и тем же значениям q1, q2, q3 (см. рис. 2.6), значения якобиана (2.16) одинаковы по значению и противоположны по знаку.
В
Н
а рис. 2.7 дана условная геометрическая интерпретация метода Ньютона, относящаяся к случаю, когда векторы ![]() и
и ![]() - одномерные. Для того, чтобы избежать многократного вычисления матрицы
- одномерные. Для того, чтобы избежать многократного вычисления матрицы ![]() , обратной матрице Якоби, можно пользоваться модифицированным методом Ньютона, при котором используется процедура, соответствующая формуле
, обратной матрице Якоби, можно пользоваться модифицированным методом Ньютона, при котором используется процедура, соответствующая формуле
где
Положение механизма, близкое к исходному, не может быть получено описанным выше способом, если определитель матрицы Якоби обращается в ноль. В рассматриваемом примере якобиан (2.16) обращается в ноль в тех положениях, при которых точки А, В и D располагаются на одной прямой (рис. 2.8). Это – особое (сингулярное) положение группы АВСD. Основываясь на данном примере, можно дать следующее определение: особое положение группы – такое, в котором якобиан обращается в ноль.
В особом положении два решения уравнения (2.11) сливаются в одно. Естественно, что в окрестностях особого положения оба решения этого уравнения оказываются близкими, и выбор одного из них становится затруднительным. Чем ближе к нулю значение якобиана, тем хуже сходятся последовательные приближения. Однако это еще не все неприятные факторы, связанные с особыми положениями. О них разговор пойдет при рассмотрении других разделов.


| Повторить по лекции 3: | |
| Термины: | |
| |
| Формулы: | |
| |
9

















