лк9 (1172701)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

А.Н.Евграфов, Г.Н.Петров. Теория механизмов и машин. Лекция 9.

2. Синтез кулачковых механизмов

Кулачковые механизмы используются и как управляющие механизмы (например, управляющие работой клапанов), и как силовые, создающие крутящий момент на валу кулака (например, кулачковые разгружатели возмущающего момента). Основными входными параметрами синтеза являются функция положения толкателя или создаваемый кулачковым разгружателем крутящий момент; дополнительными параметрами синтеза – максимально допустимый угол давления в высшей кинематической паре [α] или минимально допустимый радиус кривизны профиля кулака ρ_min. Выходными параметрами синтеза являются размеры кулачкового механизма и координаты профиля кулака.

При проведении синтеза кулачковых механизмов можно выделить три этапа:

1. Выбор закона движения толкателя (или функции положения; обычно ее записывают в виде: s = s (q), где s – перемещение толкателя, рис. 3.8);

2. Определение минимальных размеров механизма (радиуса начальной шайбы r₀, эксцентриситета е);

3. О
   пределение профиля кулака.

Рассмотрим более подробно эти этапы.

I
этап. В законе движения толкателя можно выделить в общем случае четыре фазы, которые представлены на циклограмме (рис. 3.9): удаления, дальнего стояния, возвращения и ближнего стояния. На фазе удаления происходит перемещение толкателя из самого ближнего к кулаку положения. На фазе возвращения толкатель возвращается в ближнее положение. На фазах дальнего и ближнего стояния перемещения толкателя не происходит. Выбор закона движения толкателя проводится для фаз удаления и возвращения.

Четырем фазам соответствуют углы поворота кулака: q_I, q_II, q_III, q_IV. В некоторых механизмах (например, кулачковых разгружателях) фаза q_II или q_IV может оказаться равной 0. Углы q_I, q_II, q_III, q_IV обычно определяются технологическим процессом, для которого проектируется механизм, и поэтому являются заданными. Также заданным является ход толкателя – S_max.

Обычно выбирают не саму функцию s(q), а ее вторую производную – аналог ускорения s”(q). Самая простая функция s”(q) – ступенчатая (рис. 3.10, а). Рассмотрим ее.

В
ведем единичную функцию :

(3.12)

Тогда s”(q), q’(q) и s(q) можно записать в следующем виде:

(3.13)

Здесь С₁ и С₂ – постоянные интегрирования, которые найдем из начальных условий:

q = 0, s(0) = 0, s’(0) = 0. Отсюда С₁ = 0, С₂ = 0. Для отыскания амплитуды а₀ воспользуемся условием: s(q_I) = s_max, следовательно:

,

(3.14)

Зная амплитуду а₀, можно построить графики функций s(q) и s’(q) (рис. 3.10, б и в).

Н
едостаток рассмотренного закона – скачок аналога ускорения (и, следовательно, ускорения) при q = 0, q = q_I/2 и q = q_I, что приводит к скачкообразному изменению сил инерции толкателя в этих положениях и появлению ударной нагрузки на механизм. Скачкообразное изменение ускорения называют мягким ударом. (Существует понятие и жесткого удара, при котором скачкообразно изменяется скорость толкателя, при этом ускорение стремится к бесконечности.) Для избежания ударной нагрузки используют синусоидальный закон изменения аналога ускорения (рис. 3.19).

Обозначив амплитуду аналога ускорения а₀, запишем s”(q), s’(q) и s(q) в виде:

(3.15)

Найдем постоянные интегрирования из условий: s(0) = 0, s’(0) = 0. Отсюда следует, что С₂ = 0, . Подставляя значение С₁, перепишем аналог скорости в виде:

(3.15’)

Максимальный ход толкателя s = s_max будет в конце участка удаления, т.е. при q = q_I. Подставляя s(q_I) = s_max в выражение для перемещения толкателя, получим значение амплитуды a₀:

. (3.16)

Из сравнения выражений (3.16) и (3.14) видно, что безударная работа кулачкового механизма достигается за счет увеличения амплитуды а₀ в раза.

Иногда задается момент, который должен создавать кулачковый механизм на валу кулака. Например, при проектировании разгружателя возмущающего момента задается значение возмущающего момента в виде:

(3.17)

где - амплитуда – й гармоники, – ее фаза. Разгружатель должен быть спроектирован так, чтобы обеспечивалось выполнение условия:

(3.18)

г

В

де М_р – момент кулачкового разгружателя. В качестве разгружателя выберем механизм с плоским толкателем (рис. 3.12, а).

На кулак 1 действует толкатель 2 силой R_21, которая направлена по нормали к плоскости тарели толкателя. Сила R₂₁ создает момент М_р относительно оси вращения кулака 0, равный:

М_р=R₂₁h (3.19)

Для того чтобы найти плечо h силы R₂₁, построим план скоростей механизма (рис. 3.12, б). Из подобия треугольника плана скоростей и треугольника ОАВ на плане механизма следует соотношение:

, (3.20)

отсюда найдем h:

(3.21)

Толкатель прижимается к кулаку пружиной сжатия жесткостью с, которая при сжатии создает усилие, пропорциональное жесткости и деформации: с(s₀+s), где s₀ – первоначальное поджатие пружины. Для статической модели, без учета сил трения, сил тяжести и сил инерции, сила, с которой толкатель действует на кулак, равна силе упругости пружины, т.е.

. (3.22)

С учетом (3.21) и (3.22) условие (3.18) запишем в виде:

(3.23)

Разделяя переменные в (3.23) и интегрируя, получим:

, (3.24)

где С₁ – постоянная интегрирования. Обозначим , получим закон перемещения толкателя в виде:

(3.24)

Постоянную интегрирования С₁ выбираем так, чтобы подкоренное выражение в (3.24) при любом q было неотрицательным. На этом заканчивается первый этап и начинается второй.

II этап. Определение минимальных размеров кулачкового механизма.

Р
ассмотрим пример с остроконечным поступательно движущимся толкателем (рис. 3.13, а). В таком механизме надо выбрать минимальный радиус r₀ начальной шайбы и эксцентриситет e (расстояние от линии действия толкателя до оси вращения кулака). В этом механизме уменьшение радиуса r₀ приводит к увеличению угла давления ; при большом угле давления, как говорилось в лекции 6, возможно заклинивание механизма. Поэтому минимальные размеры механизма выбирают из условия ограничения «сверху» угла давления.

Рассмотрим графический метод. Исключая q из полученных функций s(q) и s’(q), построим в координатах s’0₁s две кривые, называемые характеристиками угла давления: в первой четверти – для фазы возвращения, а во второй – для фазы удаления (рис. 3.13, б). Отметим, что аналог скорости толкателя s’(q) для вращающегося кулака и поступательно движущегося толкателя измеряется в единицах длины, так же, как и перемещение толкателя s(q). Масштаб по осям s и s’ должен быть одинаковым!

Обозначим: [_у], [_в] – допустимые углы давления на фазе удаления и возвращения соответственно. Проведем касательный к характеристикам угла давления под углами к вертикальной оси: [_у] – на фазе удаления, [_в] – на фазе возвращения. Касательные пересекутся в некоторой точке О. Если радиус начальной шайбы выбрать равным длине отрезка ОО₁, а эксцентриситет е – равным расстоянию от точки О до вертикальной оси (см. рис. 3.13, б), то получим минимально возможные размеры, при которых ни одно значение угла давления на фазе удаления и на фазе возвращения не превышает допустимых [_у] и [_в], причем в двух положениях максимальные значения углов давления равны [_у], [_в] (а именно в тех положениях, в которых касательные касаются характеристик угла давления). Если начало отрезка r₀ выбрать в заштрихованной области, то радиус начальной шайбы кулака увеличится, а максимальные значения угла давления уменьшатся. Поэтому, в частности, округлять значение r₀ следует в бơльшую сторону.

Нужно отметить, что такие построения выполняют для реверсивных механизмов, т.е. таких, в которых возможно изменение направления вращения кулака. В этом случае профиль удаления кулака становится профилем возвращения и наоборот. В нереверсивных механизмах характеристику угла давления на фазе возвращения не строят, т.к. при опускании толкателя даже при большом угле давления заклинивания не происходит. В этом случае начало О отрезка r₀ выбирают либо на пересечении касательной с вертикальной осью (для центральных механизмов, в которых е = 0), либо слева от касательной на произвольно выбранном расстоянии е от вертикальной оси (для внецентренных механизмов). В последнем случае за счет введения эксцентриситета габариты механизма становятся меньше.

Рассмотрим пример с кулачковым механизмом с плоским толкателем. В таком механизме угол давления всегда постоянный, в частности, равен 0, как на рис. 3.14, а, поэтому внутренние условия передачи сил благоприятные, опасности заклинивания нет. Однако п

С

О₁

лос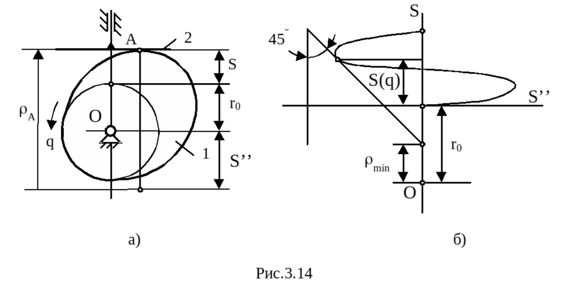
кий толкатель не может контактировать с вогнутым участком профиля кулака (рис. 3.15), поэтому заданная функция перемещения толкателя s(q) воспроизводится с ошибками. Ч
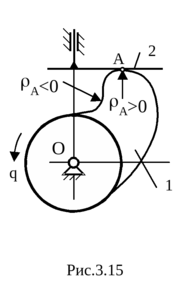
ем меньше радиус начальной шайбы r₀, тем меньше радиус кривизны ρ профиля кулака; при некоторых значениях r₀ он может стать нулевым или даже отрицательным (ρ<0), профиль становится вогнутым. Следовательно, минимальные размеры кулака выбираются из условия допустимого радиуса кривизны ρ_min.

Рассмотрим графический метод определения радиуса начальной шайбы. Можно показать, что радиус кривизны ρ_А в точке контакта А определяется следующей суммой (см. рис. 3.14, а):

(3.25)

Для того, чтобы выполнялось условие ρ_А > 0, надо, чтобы

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов лекций