Теория подобия и анализ размерностей (2012) (849561), страница 6

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 6)

3.2 Понятие и определение подобия физических явлений

Впервые с понятием подобия мы встречаемся в геометрии, когда изучаем подобные геометрические фигуры. Известно, что геометрически подобные фигуры обладают тем свойством, что их соответственные углы равны, а сходственные стороны пропорциональны (рис. 3.1).

Рис. 3.1 Подобие треугольников

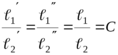, (3.1)

где: , , – линейные размеры (длины сторон) одной фигуры; , , – сходственные линейные размеры другой фигуры.

Коэффициент пропорциональности обычно называют константой подобия.

Очевидно, что условие (3.1) представляет собой математическую формулировку наличия геометрического подобия. Оно должно выполняться для любых сходственных отрезков подобных фигур, например высот, биссектрис, медиан и т. д.

Как и в случае геометрического подобия, можно установить подобие любых физических явлений: кинематическое подобие течения двух потоков газа; тепловое подобие двух процессов теплообмена; динамическое подобие сил, вызывающих подобные между собой движения. При этом необходимо выявить те условия, которые обеспечивают достоверность наличия факта подобия.

Если речь идет о подобии физических явлений, то оно может иметь место лишь между явлениями одной и той же физической природы, такие явления качественно одинаковы и описываются одинаковыми уравнениями. Могут иметь место случаи, когда форма математического описания двух физических явлений одна и та же, но они различны по своей физической сущности, то есть разнородны. В этом случае можно вести речь лишь об аналогии между ними, но подобие между такими явлениями отсутствует. В качестве примеров можно привести электрогидродинамическую аналогию и аналогию между диффузией и теплопроводностью.

Подобные физические явления развиваются в геометрически подобных пространствах. Это означает, что физическому подобию должно обязательно сопутствовать геометрическое подобие объектов и окружающей среды. Нельзя искать подобие между процессами обтекания цилиндра, сферы, плоской пластины.

Анализируя подобные физические явления, необходимо сравнивать между собой (сопоставлять) лишь однородные величины в сходственных точках пространства и в сходственные моменты времени. Однородными называются величины, имеющие один и тот же физический смысл и одинаковую размерность.

В геометрически подобных пространствах к сходственным точкам относятся те, координаты которых связаны между собой соотношениями подобия:

, , ,

где – константа подобия линейных размеров. Два момента времени и считаются сходственными, если они имеют общее начало отсчета и связаны между собой преобразованием подобия .

Подобие двух физических явлений будет иметь место только тогда, когда подобны все характеризующие их величины:

, (3.2)

что означает пропорциональность любой величины одного явления однородной величине другого явления в сходственные моменты времени в сходственных точках пространства. Коэффициент пропорциональности при этом называется постоянной подобия или множителем подобного преобразования величины . При этом не зависит ни от координат, ни от времени.

Известно, что состояние большинства физических объектов однозначно описывается конкретной величиной таких параметров, как давление, температура, теплопроводность, вязкость, скорость и т. д. Причем в разных точках объекта или потока жидкости и газа эти величины могут иметь различные значения. Совокупность этих значений в некоторый момент времени для какого-нибудь параметра определяет его поле: поле температуры, поле давления, поле скоростей и т. д. Тогда для наличия подобия двух физических явлений необходимо подобие полей всех величин, т. е. для каждой характерной величины должно быть выполнено условие вида (3.2):

; ; ; ; и т. д.

При этом каждая физическая величина может иметь свою константу подобия , отличную от других численно.

При геометрическом подобии численные значения констант преобразования для сходственных поверхностей и объемов связаны с численным значением константы преобразования линейных размеров простыми соотношениями:

; _, (3.3)

т. е. константа преобразования площадей численно равна квадрату константы преобразования линейных размеров, а для объемов, как видно из (3.3), – кубу. Для сложных физических явлений, определяемых большим числом переменных и параметров, константы подобия должны выбираться не произвольно, а с учетом всех дополнительных условий, которые определяются первой теоремой подобия.

Говоря о подобии физических явлений, необходимо отметить, что каждая физическая величина имеет свою постоянную подобия . Поэтому для того, чтобы знать, к какой конкретно величине относится константа подобия, ее принято снабжать подстрочным индексом. Таким образом, подобие двух или нескольких физических явлений означает в принципе подобие полей одноименных физических величин, для каждой из которых будет существовать своя константа подобия: и т. д. Полное сочетание всех величин, характеризующих изучаемое явление, может быть определено, если известно математическое описание явлений.

Постоянные подобия для различных величин в подобных явлениях нельзя выбирать произвольно, ибо между ними существуют строго определенные зависимости, вид которых выводится из анализа математического описания процессов, чаще всего путем образмеривания уравнений, описывающих изучаемый физический процесс. Эти соотношения занимают центральное место в теории подобия, ибо они постулируют наличие особых величин – инвариантов, которые принято называть критериями подобия.

Критерии подобия это определенные безразмерные комплексы и симплексы, составленные из параметров, характеризующих подобные явления, которые для всех подобных явлений сохраняют одно и то же численное значение.

Их главным характерным свойством является нулевая размерность. Обычно критерии подобия принято называть именами ученых, внесших большой вклад в соответствующие области науки, и обозначать двумя начальными буквами их фамилий, в некоторых случаях они обозначаются просто буквами: Re – число Рейнольдса (Reynolds), Nu – критерий Нуссельта (Nusselt) и т. д. Обычно индексы не указываются, а идемальность (одинаковость) критериев подобия у подобных явлений записывают так: .

3.3 Зависимые и независимые переменные. Условия однозначности.

Известно, что любой физический процесс может быть описан системой основных уравнений и однозначных для решаемой задачи краевых условий тогда, когда система уравнений замкнута. Лишь в этом случае возможно получить конечное решение относительно любой из неизвестных, ибо число уравнений у замкнутой системы равно числу неизвестных. Это означает, что мы в состоянии выразить интеграл системы уравнений, описывающий рассматриваемый процесс, в виде некоторой явно выраженной функции

, (3.4)

где – искомая неизвестная (зависимая) переменная; – независимые переменные, входящие в условия однозначности либо определяемые по ним из основных уравнений.

Сложность состоит в том, чтобы выяснить, какие из входящих в уравнение переменных величин относятся к независимым. Для этого требуется проанализировать условия протекания процесса:

_{- геометрию пространства, в котором развивается процесс, включая и используемую систему координат;}

_{- существенные для изучаемого процесса физические характеристики тел (веществ), входящих в систему (участвующих в процессе);}

_{- начальное и конечное состояние системы;}

_{- условия на границах, охватывающие систему, на всем временном протекании процесса.}

Нетрудно заметить, что перечисленное представляет собой расширенный перечень краевых условий. В теории подобия их принято называть условиями однозначности рассматриваемого (изучаемого) физического явления. На основании этого напрашивается очевидный вывод о том, что все другие переменные, входящие в систему уравнений, будут относиться к независимым переменным.

Обобщая изложенное в параграфе, отметим, что величины в выражении (3.4) составлены из условий однозначности.

_{3.4 Теория подобия}

Основные положения теории подобия можно сформулировать тремя теоремами.

Первая теорема подобия

Подобные физические явления и процессы имеют одинаковые критерии подобия.

Одинаковость критериев подобия для гидродинамики течения обычно записывается следующим образом

.

Или для процессов вынужденной конвекции

,

где 1, 2, …, n индексы подобных между собой явлений.

_{Вторая теорема подобия}

Характеристики

Список файлов книги