практикум_механика (1) (1106030), страница 21

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 21)

7. Вычислить момент инерции каждого из маятников по формуле (5), подставив в нее значения, полученные в п.6.

8. Вычислить теоретическое значение момента инерции каждого из маятников по формуле (7).

Эксперимент 2. Измерение силы натяжения нити подвеса маятника Максвелла (с помощью динамометра)

1. Насадив до упора на диск самое узкое кольцо с массой , произвести по динамометру отсчет силы натяжения нити во время движения маятника и затем силы натяжения нити в момент рывка в нижней точке. Измерения повторить не менее 5 раз. Аналогичным образом произвести измерения для маятников с другими кольцами. Результаты занести в таблицу 4 и таблицу 5.

2. Произвести вычисление по формуле (12).

3. Сравнить результаты с экспериментом 1.

4. Вычислить момент инерции каждого из маятников по формуле (5), подставив в нее экспериментальные значения, взятые из таблицы 4.

Таблица 4

Таблица 5

Произвести статистическую обработку всех полученных результатов и сравнить результаты двух экспериментов.

ЛАБОРАТОРНАЯ РАБОТА 10

ИССЛЕДОВАНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ РЕЗОНАНСА

Цель работы: Изучение волновых процессов на примере стоячих волн смещений в натянутой струне. Определение собственных частот колебаний струны при различном ее натяжении. Определение скорости распространения волны по струне.

Оборудование: стойка со струной, механизмом ее натяжения и вибратором, генератор звуковых частот, набор грузов, линейка, микрометр, весы.

Краткая теория.

Задачей настоящей работы является исследование колебаний струны, представляющей собой гибкую упругую однородную натянутую нить. Пусть струна длиной натянута вдоль оси (рис.1). Пусть ее правый конец закреплен неподвижно в точке , а левый конец, совпадающий с началом координат, приведен в колебательное движение вдоль оси 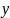(точка ).

Е сли точка совершает гармоническое колебательное движение вдоль оси 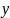с частотой по закону

Рисунок 1.

то от нее вдоль струны распространяется поперечная волна со скоростью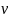 . Точка струны, находящаяся на расстоянии 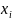от начала координат, будет иметь в момент времени 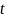такое же смещение 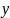, какое точка имела раньше, в момент времени 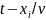. Знак минус означает отставание во времени (запаздывание). Величина запаздывания 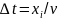– это время, необходимое для распространения волны на расстояние 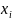. Следовательно, при распространении волны по направлению от к (прямая волна) точка струны с координатой 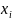будет колебаться по закону

Достигнув точки , волна отразится и начнет распространяться в обратном направлении. Пусть путь, пройденный волной от точки до точки 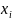с учетом ее отражения в точке , равен . Следовательно, выражение смещения этой точки для отраженной волны запишется в виде

где – сдвиг фазы, возникающий при отражении волны. Как показано в приложении 1 величина при отражении от закрепленного конца струны. С учетом этого условия функция (1) примет вид уравнения

показывающего, что при отражении от закрепленного конца струны волна смещения частиц меняет знак. Она отстает по фазе на угол , что эквивалентно отставанию на полволны (говорят о потере полуволны при отражении).

Результирующее смещение точки под действием прямой и обратной волн является результатом суперпозиции этих волн:

Уравнение (2) описывает движение любой точки струны. Отметим, что каждая точка колеблется по гармоническому закону. Различные точки колеблются с различными амплитудами

так как амплитуда является гармонической функцией координаты точки .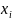

В точках, для которых , то есть аргумент

амплитуда колебаний . Эти точки все время остаются в покое. Их называют узлами смещений. Прежде всего, таким узлом является закрепленный конец струны (точка , для которой ). Следующие узлы смещений лежат на расстоянии друг от друга (рис.2). Это расстояние находится из условия или

то есть узловые точки отстоят на расстояние полуволны друг от друга. Точки, лежащие между узлами смещений, имеют амплитуду не равную нулю. При этом в точках, для которых , то есть аргумент

амплитуда смещений достигает максимальной величины . Эти точки называются пучностями смещений. Расстояние между ними, как и между узлами, равно . Фаза смещений всех точек, расположенных между двумя соседними узлами, одна и та же. При переходе через узел фаза смещений меняется на , то есть точки, расположенные по разные стороны от узла, колеблются в противофазе.

Рисунок 2.

В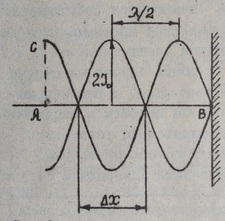 олна с таким распределением амплитуд и фаз называется стоячей волной. Рассмотрим, как амплитуда смещения 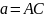произвольной точки связана с амплитудой 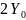волны в пучности (рис.2). Если фиксировано, то амплитуда волны в пучности зависит от расстояния точки от узла. Действительно, если точка расположена на расстоянии 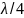от узла, то есть в пучности, то амплитуда ее смещения 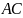равна амплитуде волны 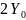. Из рис.2 и уравнения (2) видно, что по мере приближения точки к узлу волны амплитуда ее смещения будет уменьшаться. Чтобы величина 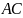по мере приближения к узлу смещения оставалась постоянной, как мы условились, необходимо увеличивать амплитуду волны 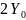. Максимальное возможное значение 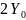равное «бесконечности» потребуется, когда точка окажется в узле волны.

Таким образом, мы приходим к условию получения стоячей волны с большой амплитудой смещений. Это условие заключается в том, что на обоих концах струны должны находиться узлы смещений. При этом в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз. Это условие можно записать в таком виде

где 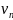– частота колебаний струны. В результате получим

Рисунок 3.

Т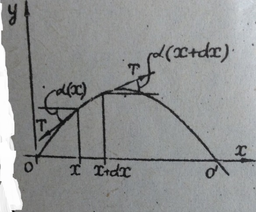 аким образом, чтобы получить большие амплитуды колебаний (резонанс), нужно подобрать для данной струны частоты таких колебаний, которые удовлетворяют соотношению (3). Такие частоты 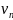называются собственными частотами колебаний струны. Они оказываются кратными частоте основной гармоники 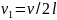, которой соответствует .

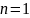В общем случае на струне одновременно могут устанавливаться стоячие волны с различными собственными частотами.

Чтобы перейти к экспериментальным исследованиям, необходимо предварительно установить, какие внешние факторы влияют на характер колебаний струны. Рассмотрим в качестве примера колебания гибкой однородной струны с закрепленными концами (рис.3). Струну расположим горизонтально вдоль оси и совместим левый ее конец с началом координат. Ось направим по вертикали. Рассмотрим движение отрезка струны с координатами и . Обозначим через силы натяжения, действующие на этот участок струны, а через и соответствующие углы наклона этих сил к оси . 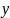Проекции сил на ось можно записать в виде

Разность этих проекций есть результирующая сила, определяющая движение рассматриваемого отрезка струны. По второму закону Ньютона она должна быть равна произведению массы элемента струны на его ускорение

Здесь – объемная плотность материала струны, а – ее диаметр. Разделив обе части выражения (4) на , получим

Уравнение (5) имеет общий вид

и называется волновым уравнением, а коэффициент 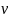определяет скорость распространения волны.

Уравнению (6) удовлетворяет функция

описывающая распространение вдоль оси поперечной волны. Здесь – волновое число, показывающее, сколько длин волн укладывается в отрезке пути длиной . Длина волны равна расстоянию вдоль оси между двумя соседними элементами струны, колеблющимися в одной фазе.

Легко доказать подстановкой, что уравнению (5) удовлетворяет не только функция (7), описывающая бегущую поперечную волну, но и функция (2), описывающая стоячую волну.

Характеристики

Список файлов книги