практикум_механика (1) (1106030), страница 19

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 19)

Это условие накладывает ограничение на величину момента внешних сил, вызывающих прецессию. Он должен быть меньше, чем кинетическая энергия собственного вращения гироскопа. Очевидно, что чем больше угловая скорость , тем лучше выполняется это неравенство, то есть тем ближе движение гироскопа к тому, которое предсказывает приближенная теория.

Второе ограничение связано с тем, что, рассматривая прецессию, мы пренебрегли трением. В действительности прецессионное вращение с частотой вызывает появление момента сил трения противоположного по направлению вектору (рис.1) и стремящегося затормозить это вращение. Этот момент , приведет к тому, что вектор не будет просто описывать окружность вокруг оси , так как его конец будет опускаться под действием , вызывая приращение . Наблюдателю будет казаться, что это сила вызывает опускание конца оси гироскопа. Чтобы убедиться в том, что сила здесь не причем, можно рукой слегка притормаживать прецессию или помогать ей, подталкивая диск в сторону его вращения (рис.4). Подъем или опускание стержня 7 вследствие этих действий показывает, что гироскоп действительно «подчиняется» моментам, а не силам.

Из сказанного ясно, что для применимости нашего рассмотрения необходимо, чтобы трение в подшипниках на рис.1 и рис.4 было достаточно малым. Что касается трения в оси электрического гироскопа, то в установке оно компенсируется электромотором, так что . Однако в случае вращения по инерции (рис.5) это трение будет уменьшать , что необходимо иметь в виду при выполнении работы (частота прецессии не остается постоянной).

Порядок выполнения работы

1. Установите гироскоп (рис.4) горизонтально по уровню с помощью винтовых ножек. Отбалансируйте его, то есть найдите такое положение груза массы , при котором гироскоп находится в безразличном положении и запишите значение положения груза по шкале 7 (нулевой отсчет). При хорошей балансировке при горизонтальном положении рычага 7 (рис.4) ось гироскопа не должна поворачиваться вокруг горизонтальной оси при легком постукивании по стойке.

2. Включите электронный блок гироскопа нажатием клавиши СЕТЬ. Включите мотор гироскопа поворотом ручки 2 по часовой стрелке (рис.4) и установите некоторую частоту вращения ротора по индикатору 1. Выждите 1-2 минуты, чтобы частота вращения установилась. Нанося легкие удары рукой по рычагу 7, убедитесь, что ось гироскопа не изменяет своего положения в пространстве. Объясните причину устойчивости оси гироскопа.

3. Закрепив диск и снова постукивая по рычагу 7, убедитесь, что ось гироскопа, лишенного одной из степеней свободы (возможности вращаться вокруг вертикальной оси), теряет устойчивость. Почему?

4. Придерживая рукой рычаг 7, сдвиньте груз массы из равновесного положения на некоторую величину . Это вызовет прецессию гироскопа. Трение в оси (какой именно?) приводит к тому, что рычаг 7 будет медленно опускаться. Измеряя угловую скорость опускания рычага (по времени поворота на некоторый угол) оцените момент силы трения. Подталкивая диск (рис.4) по ходу его движения, пронаблюдайте подъем конца рычага 7. Объясните это явление.

5. Направьте рычаг 7 несколько вверх (под углом к горизонтали). Измерьте угловую скорость регулярной прецессии при фиксированном значении смещения груза массы вдоль рычага 7 и при фиксированном значении частоты вращения ротора гироскопа (проверьте показания индикатора 1 с помощью стробоскопа). Измерение ведите до тех пор, пока рычаг 7 не опустится на ниже горизонтали.

6. Изменив величину смещения груза массы , измерьте соответствующие скорости прецессии не менее, чем для пяти различных значений при фиксированном значении . Результаты измерений изобразите в виде графика . Пользуясь соотношением (4) и измеренным значением , найдите из этого графика значение .

7. Оцените погрешность в определении и проверьте справедливость неравенства (10).

8. При фиксированном значении , изменяя частоту вращения с помощью ручки 2, измерьте соответствующие угловые скорости не менее, чем для пяти различных значений (проверяйте показания индикатора 1 с помощью стробоскопа). Постройте график зависимости от и найдите из этого графика значение с помощью соотношения (4). Сравните результат со значением, полученным в п.6.

9. При помощи нити, сообщите ротору простого гироскопа быстрое вращение и измерьте частоту его вращения с помощью стробоскопа. Осторожно положив головку гироскопа в лунку подставки и слегка подтолкнув его, измерьте с помощью секундомера угловую скорость его прецессии по времени 5-10 полных оборотов. Сняв гироскоп с подставки, еще раз измерьте стробоскопом уменьшившуюся частоту его вращения . С помощью торсионного подвеса измерьте момент инерции запасного ротора по методу, изложенному в теории. Измерив массу гироскопа с оправой 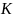(рис.5) и расстояние от центра опорной головки до центра тяжести , проверьте справедливость соотношения (5), взяв в качестве среднее арифметическое . Проверьте, выполняется ли неравенство
(10).

10. Повторите измерения не менее пяти раз. Оцените точность, с которой выполняется соотношение (5) при условии выполнения неравенства (10).

ЛАБОРАТОРНАЯ РАБОТА 9

ИЗУЧЕНИЕ ДВИЖЕНИЯ МАЯТНИКА МАКСВЕЛЛА И ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ С ЕГО ПОМОЩЬЮ

Цель работы: Изучение законов вращательного движения твердого тела (диск Максвелла). Определение момента инерции диска и силы натяжения нити при его движении

Оборудование: экспериментальная установка с маятником Максвелла, набор сменных колец, штангенциркуль, весы, секундомер

Краткая теория.

Рисунок 1.

Маятник Максвелла, показанный на рис.1, представляет собой однородный диск , прочно насажанный на металлический стержень . Для изменения момента инерции маятника на него надеваются сменные кольца 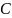. Диск Максвелла подвешивается на двух нитях к верхней опоре .

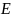Наматывая нити, виток к витку на стержень , поднимают диск к опоре 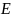. Если теперь диск отпустить, он начинает снижаться с возрастающей скоростью, одновременно увеличивая и угловую скорость вращения вокруг своей оси. В нижней точке маятник меняет направление поступательного движения на обратное, продолжая вращаться по инерции. Нить начинает снова наматываться на стержень и маятник, теряя скорость, поднимается вверх. Остановившись в некоторой точке, диск снова начинает двигаться вниз, вращаясь в противоположную сторону. Смена направления движения в нижней точке сопровождается резким изменением натяжения нити – рывком. «Колебания» маятника постепенно затухают (высота поднятия диска уменьшается) за счет действия сил трения.

Если не учитывать силы трения, то уравнение движения маятника в проекции на ось у будет иметь вид

Рисунок 2.

Здесь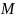 – масса маятника, 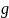– ускорение свободного падения, – сила натяжения одной нити, – ускорение поступательного движения центра масс маятника. Для упрощения нить считается невесомой и нерастяжимой. Все приведенные выше величины показаны на рис.2.

В соответствии с основным законом динамики вращательного движения можно записать

где – момент инерции маятника относительно оси симметрии, – радиус стержня , – угловое ускорение маятника.

Связь между угловым и линейным ускорениями определяется известным соотношением

Ускорение поступательного движения можно найти из уравнения кинематики равноускоренного движения центра масс маятника, устанавливающего связь между временем 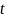движения маятника и высотой , на которую опускается его центр масс

Решая совместно уравнения (2)-(4), легко получить выражения для момента инерции маятника

Заменив радиус цилиндрического стержня на его диаметр , получим окончательное выражение

Формула (5) позволяет определить момент инерции маятника Максвелла. При этом сила натяжения нити может быть измерена экспериментально, либо получена теоретически совместным решением уравнений (1) и (4)

где 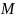– полная масса маятника Максвелла.

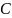Величина момента инерции маятника Максвелла находится путем суммирования моментов инерции цилиндрического стержня , центрального диска и сменного кольца , насаживаемого на диск . Таким образом, теоретическое значение момента инерции маятника определяется формулой

где

, , – массы стержня, диска и кольца соответственно; , , – диаметры стержня, диска и внешний диаметр кольца соответственно.

Рисунок 3.

Представляет интерес рассмотрение движения маятника Максвелла в нижней точке траектории, когда он меняет направление своего поступательного движения. Оно сопровождается рывком из нити, при котором ее натяжение резко увеличивается. Величину натяжения резко увеличивается. Величину натяжения можно оценить теоретически.

В нижней точке своего поступательного движения весь маятник (не показан на рис.3) и его ось (показанная на рисунке) останавливаются и начинают поворачиваться вокруг этой точки. При этом, например, ее внешняя точка описывает полукруг диаметром , поочередно занимая положения , . С момента, когда точка займет положение , ось маятника, двигаясь по инерции, начинает накручивать на себя нить, а маятник поднимается вверх.

Скорость маятника в нижней точке достигает своего максимального значения

Характеристики

Список файлов книги