практикум_механика (1) (1106030), страница 15

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 15)

Свободные колебания системы

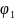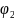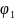Пусть в некоторый момент времени первый маятник отклонен от вертикали на угол , а второй – на угол . Как видно из рис.1, при этом одна пружина растягивается, а другая сжимается на одинаковую величину . Первая пружинка действует на стержень второго маятника в точке силой по направлению к точке , а вторая пружинка действует не него в той же точке с силой , направленной от к . При малых углах и 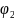обе эти силы будут приблизительно перпендикулярны к стержню второго маятника, а их сумма равна

где обозначает «совместную» жесткость обеих пружин

.

По третьему закону Ньютона на конец стержня действует сила , направленная к точке , а на конце возникает сила , равная и противоположная по направлению силе , действующей в точке . Обе эти силы можно считать приложенными к стержню первого маятника в точке 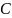(перенося их параллельно вдоль стержня ). При малых углах отклонения и в сумме дают силу , приблизительно перпендикулярную стержню маятника 1 и равную по величине (1).

При малых углах отклонения, деформация пружинок пренебрежимо мало отличается от длины дуги окружности радиуса , равного расстоянию от точек 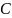и до точки подвеса . Поэтому

где подразумевается, что 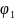и 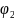измерены в радианах.

Уравнения движения маятников относительно горизонтальной оси, проходящей через точку , имеют вид:

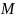Здесь – момент инерции каждого из маятников относительно рассматриваемой оси, – угловое ускорение, – момент силы тяжести, – момент силы взаимодействия. При малых углах отклонения

где обозначает расстояние от точки до центра тяжести каждого из маятников, а минусы соответствует тому, что и стремятся уменьшить 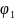и 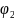соответственно.

Из рис.1 видно, что вращает первый маятник в ту же сторону, куда он отклонен (стремится увеличить 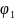), в то время как действует в противоположную строну и стремится уменьшить 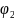. Учитывая это обстоятельство соответствующим выбором знаков, подставив (2) в (1) и умножив силы и на плечо , получим

Подставляя значения моментов сил в уравнения движения (3), перенося все члены в левую часть и группируя подобные члены, получим систему уравнений следующего вида:

Введем обозначения

и поделив почленно уравнения (4) на , перепишем их в виде

Величина является частотой собственных колебаний каждого из физических маятников 1 и 2 при отсутствии связи между ними, то есть при (см лабораторную работу № 5). Величину называют константой связи; из (5) видно, что она пропорциональна общему коэффициенту жесткости пружин связи и квадрату «плеча силы связи» . Можно показать, что уравнения движения любой колебательной системы при малых смещениях из положения равновесия можно записать в виде (6).

Произведем простое преобразование системы уравнений (6), а именно, сложим и вычтем эти уравнения почленно и введем новые переменные

которые называются нормальными координатами. Из (6) получим следующие уравнения для и :

Первое из этих уравнений описывает гармонические колебания с частотой , а второе – тоже гармонические колебания, но с частотой . Эти колебания называются нормальными колебаниями (или модами), а соответствующие частоты и – нормальными частотами системы. Подчеркнем, что нормальные колебания, в отличие от (6), независимы между собой.

Если обозначить амплитуды нормальных колебаний через и , а их начальные фазы через и , то общее решение каждого из уравнений (7) можно записать в обычном виде:

Поскольку, как легко видеть из определения и ,

мы получаем следующий результат: движение колебательной системы (при малых отклонениях от равновесия) является суперпозицией (наложением) нормальных (независимых) гармонических колебаний с частотами и , причем, согласно (7),

Таким образом, общее решение уравнений движения системы (4) получается подстановкой в (8) выражений для и :

Постоянные , , и должны быть определены из начальных условий. Мы будем предполагать, что маятники приводятся в движение с помощью начальных отклонений (без толчков). Это означает, что их скорости равны нулю в начальный момент времени , то есть

Таким начальным условиям в решении (10) соответствует выбор начальных фаз , то есть

Полагая здесь и выражая и через начальные отклонения и первого и второго маятников, получим окончательно:

Рассмотрим несколько характерных случаев возбуждения колебаний системы.

Синфазное возмущение колебаний системы

Пусть в начальный момент оба маятника были отклонены в одну сторону на одинаковый угол , после чего их одновременно отпустили. Движение системы будет тогда описываться формулами (11), в которых надо положить , то есть

Отсюда видно, что в этом случае в системе возбуждается только одно нормальное колебание с частотой , которая согласно (9) равна собственной частоте колебаний каждого из маятников в отсутствие связи между ними. Из полученных выражений видно, что маятники колеблются «вместе» и синхронно, тождественно равно нулю, то есть пружины связи не деформируются и не влияют на движение маятников (что и объясняет равенство ). Такое нормальное колебание называют синфазным (синфазная мода).

Противофазное возбуждение колебаний системы

Если в начальный момент маятники отклоняются в противоположные стороны на одинаковый угол и одновременно отпускаются, в решении (11), то есть

Полученные выражения показывают, что в системе опять возбуждается одно нормальное колебание, но на этот раз с , которая, согласно (9), равна . В этом случае маятники колеблются в противофазе (со сдвигом фаз ), их отклонения противоположны по знаку во все время движения, а скорости противоположны по направлению, причем пружины связи максимально деформируются (что объясняет неравенство ). Такое нормальное колебание называется антифазным (антифазная мода).

Возбуждение колебаний системы со сдвигом фаз

Пусть теперь в начальный момент при отклоняется только один из маятников, скажем первый, а второй остается в положении равновесия. Если величина этого отклонения равна , то начальные условия в (11) должны быть выбраны в виде , , то есть движение системы описывается выражениями:

С помощью элементарной тригонометрии их можно переписать в виде:

Введем обозначения

и перепишем полученные формулы:

Из полученных выражений видно, что в этом случае каждый из маятников колеблется с частотой , причем сдвиг фаз между их колебаниями равен , так как : в тот момент, когда отклонение одного из них достигает максимальной величины, второй проходит через положение равновесия (при , ) и наоборот. Однако «амплитуда» этих колебаний сама медленно периодически изменяется во времени с частотой . Такие колебания называются биениями. Например, при амплитуда второго маятника равна нулю; при , то есть через время, равное , она достигает максимального значения (за это время маятник совершит большое число колебаний). Через время , определяемое условием , амплитуда снова обращается в нуль, в связи с чем это время называется периодом биений (не путать с периодом колебаний ). Таким образом, частота биений равна .

Рассмотрение, проведенное выше, показывает, что в общем случае свободные колебания системы представляют собой биения, но при специальном выборе начальных условий можно возбудить то или иное нормальное колебание (моду).

Заметим в заключение этого раздела, что, если мы зафиксируем один из маятников, например первый, в положении равновесия (для этого, как видно из (4), к нему придется приложить внешнюю силу, чтобы скомпенсировать момент , действующий со стороны второго маятника через пружины связи), то движение одного только второго маятника будет описываться вторым из уравнений (4) или (6) с , то есть

Это тоже гармонические колебания с частотой , которая называется парциальной частотой. Как видно из (9) и (12), парциальная частота каждого из маятников расположена между нормальными частотами системы .

Вынужденные колебания системы

Чтобы исследовать вынужденные колебания в системе двух связанных маятников, добавим к ней стержень 3, который также может совершать колебания вокруг той же горизонтальной оси, проходящей через точку , вокруг которой колеблются маятники 1 и 2 (рис.2). В точке этого стержня на расстоянии от оси вращения закреплен перпендикулярно ему второй стержень , аналогичный , концы которого соединены пружинами с точкой на стержне маятника 2, причем .

Характеристики

Список файлов книги