практикум_механика (1) (1106030), страница 17

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 17)

используя нормальные частоты и , найденные в п.3 и в п.4.

Эксперимент 3. Изучение вынужденных колебаний

1. Восстановите связь маятника 2 со стержнем 3, надев вторую пару пружин на стержень 10, находящийся на стержне 3, и на вторую втулку 12 на маятнике 2 (теперь он будет связан как с маятником 1, так и со стержнем 2). Выберите плечо достаточно малым (по указанию преподавателя или лаборанта). Проверьте, что стержни 10 и втулки 12 находятся на одной высоте при равновесном положении маятников.

2. Включите двигатель, приводящий в движение стержень 3 и плавно изменяйте его частоту ручкой ЧАСТОТА КОЛЕБАНИЙ. Внимательно наблюдая за движением маятников, добейтесь (подбором частоты вращения двигателя) возбуждения синфазных нормальных колебаний (резонанс ). Когда эти колебания установятся, измерьте период колебаний маятника 2 по времени 10 колебаний. Вычислите частоту этих колебаний .

3. Продолжая увеличивать частоту вращения вала двигателя, настройте ее в резонанс с верхней нормальной модой , то есть добейтесь возбуждения чисто антифазных колебаний. Когда эти колебания установятся, измерьте их частоту (по времени 10 колебаний).

4. Попробуйте добиться резонансных биений и измерьте их частоту.

5. Повторите измерения, изменяя частоту вращения вала двигателя в широком диапазоне. Произведите статистическую обработку результатов измерения и . Сравните частоты, полученные в п.2 и в п.3 с частотами, полученными в эксперименте 2 п.3 и п.4 (при достаточно малой константе связи они должны быть приблизительно равны).

6. Зафиксируйте рукой маятник 1 в положении равновесия. Изменяя частоту вращения вала двигателя, добейтесь резонанса с парциальными колебаниями маятника 2. Измерьте частоту вынужденных колебаний . Повторите настройку и измерения несколько раз и произведите статистическую обработку результатов. Сравните Ваш результат с полученным результатом в эксперименте 2 п.2.

Представление результатов

На основании проведенных измерений следует найти (с указанием доверительных интервалов, вычисленных по разбросу экспериментальных данных, то есть на основе случайных ошибок):

1. собственную частоту (эксперимент1 п.5);

2.нормальные частоты системы и (эксперимент 2 п.3 и п.4);

3. парциальную частоту (эксперимент 2 п.2);

4. константу связи (вычисляется с помощью , и );

5. частоту биений и частоту колебаний при биениях ;

6. резонансные частоты , и (эксперимент 3 п.2, п.3, п.6).

ЛАБОРАТОРНАЯ РАБОТА 8

ИЗУЧЕНИЕ ПРЕЦЕССИИ ГИРОСКОПА И ИЗМЕРЕНИЕ УГЛОВОЙ СКОРОСТИ ЕГО ВРАЩЕНИЯ

Цель работы: Исследование основных закономерностей регулярной прецессии симметричного гироскопа в гравитационном поле Земли. Измерение угловой скорости вращения гироскопа с помощью прецессии.

Оборудование: экспериментальная установка – гироскоп.

Краткая теория.

Симметричным гироскопом называется тело вращения, быстро вращающееся вокруг своей геометрической оси. Это вращение с большой угловой скоростью либо поддерживается электромотором, либо происходит по инерции (после предварительного ускорения – разгона).

Если ось вращения гироскопа неподвижна, то его момент импульса равен:

где – момент инерции относительно оси вращения, а векторы и совпадают по направлению между собой и с осью гироскопа. Однако особенно интересно движение свободного гироскопа, ось вращения которого сама может поворачиваться и принимать любое направление в пространстве (это обеспечивается конструкцией, например, в «кардановом подвесе»). При этом одна из точек оси гироскопа обычно остается неподвижной (ее иногда называют точкой опоры гироскопа).

Движение гироскопа, как и любого твердого тела, описывается основным уравнением динамики вращательного движения (следствие второго закона Ньютона):

где – сумма моментов внешних сил, действующих на гироскоп. Следует отметить, что для свободного гироскопа равенство (1) не имеет места и векторы и уже не совпадают по направлению между собой и не направлены по оси симметрии. Например, если ось гироскопа, вокруг которой происходит его вращение с угловой скоростью , в свою очередь поворачивается вокруг оси, перпендикулярной ей, с другой угловой скоростью , то

где и – продольный и поперечный моменты инерции тела гироскопа (по отношению к его оси). В общем случае (например, для диска массы и радиуса , а ), и поэтому не параллелен вектору суммарной (мгновенной) угловой скорости . Однако, для гироскопа всегда выполняется условие . Кроме того, обычно , так что вторым слагаемым в выражении для можно пренебречь по сравнению с первым. В связи с этим мы будем считать, что равенство (1) выполняется и для свободного гироскопа, то есть вектор направлен вдоль оси вращения с угловой скоростью , даже если эта ось медленно изменяет свое положение в пространстве. В этом состоит основное приближение теории гироскопа.

Уравнение движения (2) можно переписать в виде:

где – изменение момента импульса за малый промежуток времени и – суммарный момент внешних сил.

Если , то , то есть . В соответствии с (1) это означает, что ось гироскопа сохраняет свое направление в пространстве и угловая скорость его вращения не изменяется по величине. Такой случай будет иметь место, если точка опоры гироскопа совпадает с его центром тяжести (вес компенсируется реакцией опоры), а момент сил трения компенсируется вращательным моментом электромотора (уравновешенный гироскоп).

Уравнение (3) помогает понять «необычное» поведение гироскопа при действии на него внешних сил.

Кратковременное силовое воздействие

Пусть на уравновешенный гироскоп действует некоторая сила в течение малого промежутка времени (удар, толчок), то есть . При этом из (3) следует, что , то есть . Это значит, что ось гироскопа практически не изменит своего положения, то есть при кратковременных воздействиях даже больших сил движение свободного гироскопа изменяется мало, он как бы сопротивляется попыткам изменить величину и направление его момента импульса . Заметим, что если гироскоп не вращается , то такое же воздействие (удар) просто вызовет равномерное вращение оси гироскопа с некоторой малой угловой скоростью , при котором она может сколь угодно далеко отойти от своего первоначального положения (обычное поведение в соответствии с законом инерции). Таким образом, замечательная «устойчивость» гироскопа связана с его быстрым вращением вокруг своей оси (с наличием большого момента импульса в начальный момент).

Стационарное силовое воздействие

Если в (3), то за равные промежутки времени вектор будет изменяться на равные величины . Таким образом, если поместить начало этого вектора в неподвижной точке (точке опоры), то его конец, а вместе с ним и конец оси гироскопа, вдоль которой приблизительно направлен вектор , будет двигаться равномерно (отметим, что при , то есть конец оси гироскопа двигался бы под действием постоянной силы не равномерно, а с постоянным ускорением). Такое равномерное вращение оси гироскопа под действием постоянного момента сил называется регулярной прецессией.

Другим замечательным свойством прецессии (помимо отсутствия ускорения) является то, что изменение момента импульса (движение оси гироскопа) происходит не в направлении приложенной силы , а в направлении ее момента , то есть перпендикулярно (так как ). Таким образом, гироскоп как бы «не подчиняется» силе и движется в «странном» направлении.

Чтобы получить количественные соотношения, рассмотрим подробнее регулярную прецессию свободного неуравновешенного гироскопа под действием постоянного момента силы тяжести. Для простоты возьмем гироскоп в виде однородного диска, насаженного на ось, как показано на рис.1.

Рисунок 1.

Пусть ось гироскопа, вращающегося с угловой скоростью , направлена горизонтально в начальный момент времени (его начальный момент импульса имеет приблизительно то же направление). Совместим с этим направлением ось 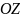неподвижной системы координат с центром в точке опоры . Конструкция свободного гироскопа должна допускать вращение его оси 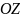вокруг двух других осей и (например, подшипник на рис.1 обеспечивает вращение вокруг вертикальной оси ).

Приложим в некоторой точке оси гироскопа постоянную силу , направленную вертикально вниз (например, подвесим в этой точке грузик массы ). Момент этой силы равен произведению на плечо и направлен вдоль оси (по правилу правого винта).

Согласно уравнению (3), приращение вектора имеет такое же направление, то есть перпендикулярно плоскости чертежа на рис.1, так как , . Поскольку , это приращение не может изменить длину вектора , а только изменяет его направление, то есть поворачивает вектор . Вместе с ним поворачивается и ось гироскопа, а, следовательно, и плечо силы . Поэтому условие сохраняется во все моменты времени. В результате вектор , оставаясь постоянным по величине, равномерно вращается вокруг оси , так что его конец описывает окружность в плоскости (рис.2).

Рисунок 2.

Угловая скорость этого вращения равна по определению , где – угол, на который вектор поворачивается за малое время . Из рис.2 видно, что в радианном измерении , так как при дуга, стягивающая угол , стремится к отрезку касательной . Таким образом,

где мы использовали (3) и (1) для и 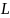, а также ввели обозначение для расстояния от точки опоры до точки приложения силы тяжести (плечо силы ). Что касается направления вектора , то из рис.1 видно, что он направлен вдоль оси , то есть .

Рисунок 3.

Рассмотрим теперь гироскоп, ось которого в начальный момент не горизонтальна, а составляет угол с вертикалью (при получим прецессию, рассмотренную выше). Пусть теперь точка опоры не совпадает с центром тяжести гироскопа 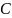, то есть прецессия вызвана не дополнительным грузом , а собственным весом гироскопа , где – масса гироскопа (рис.3).

Как и в первом случае, сила веса уравновешивается реакцией опоры в точке , но момент этой силы относительно точки равен теперь , так как плечо есть расстояние от до прямой, вдоль которой действует (а не до точки приложения этой силы). Через мы по-прежнему обозначили расстояние от точки опоры до центра тяжести. Поскольку момент силы тяжести по-прежнему направлен перпендикулярно плоскости чертежа, и согласно (3), мы снова имеем , то есть . Постоянство длины вектора означает, что ось гироскопа должна описывать конус с вершиной в точке опоры . Конец вектора будет при этом двигаться по окружности с центром в точке , а не в точке как на рис.1. Как видно из рис.3, радиус этой окружности равен .

Характеристики

Список файлов книги