практикум_механика (1) (1106030), страница 22

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 22)

Из аналогии (5) и (6) следует, что функция, удовлетворяющая уравнению (5), описывает волну, распространяющуюся с фазовой скоростью

Подставляя (8) в (3), получаем формулу для расчета собственных частот колеблющейся струны

Условия применимости метода резонанса

Рассмотрим детальные условия, при которых теория, развитая выше для движения в вакууме идеально гибкой струны, может быть применима для реальной струны.

При колебаниях реальной струны всегда происходят потери энергии (часть энергии теряется за счет трения о воздух; другая часть уходит через концы струны и т.д.). Для поддержания незатухающих колебаний необходимо воздействие на струну периодической внешней силы. Возбуждение в струне внешней гармонической силой стоячих волн носит резонансный характер. Амплитуда стоячей волны возрастает по мере приближения частоты вынуждающей внешней силы к частоте собственных колебаний струны. При совпадении частот амплитуда достигает максимума. При этом энергия, поступающая извне, должна полностью компенсировать ее потери струной за счет перехода в немеханические виды энергии. Для такой компенсации необходима передача энергии по струне.

Рассмотренная выше теория стоячих волн, развитая для случая отсутствия потерь энергии, показывает, что узлы смещения все время остаются неподвижными. При этом течения энергии по струне не происходит, так как она не может перейти через узлы. Передача энергии по струне производится только бегущей волной. Таким образом, в реальной струне должны одновременно возбуждаться стоячие и бегущие волны. В результате узлы окажутся несколько размытыми за счет движения. Если, однако, потери энергии за период малы по сравнению с ее запасом в струне, то искажение стоячих волн бегущей волной будет малым. Оценить соотношение этих энергий можно по соотношению квадратов амплитуд бегущей и стоячей волн. Первая измеряется по размытию узла, вторая – в пучности стоячей волны

<<

При наблюдении стоячих волн в эксперименте можно заметить, что струна не колеблется в одной плоскости, а совершает вращательное движение вокруг положения равновесия. Однако, вращение может быть представлено как сумма колебаний в двух взаимно перпендикулярных плоскостях. В результате, все полученные выше соотношения остаются в силе. Наконец, заметим, что величины, определяемые формулами (8) и (9), не зависят от модуля сдвига материала струны. Такой результат является следствием того, что мы пренебрегли упругой деформацией этого материала, то есть изменением силы натяжения при колебаниях.

Без доказательства заметим, что это допущение в условиях нашего эксперимента не искажает заметно физической картины и сделанных выводов, поскольку сдвиговые напряжения малы по сравнению с силой натяжения струны.

Описание экспериментальной установки и методики измерений

В лабораторной работе колебания возбуждаются в медной однородной струне, закрепленной вертикально. Схема установки показана на рис.4. Установка состоит из трех основных частей: вибратора, струны и механизма натяжения. Внешнее периодическое воздействие на струну осуществляется в верхней точке струны, где ее конец прикреплен к плоской пластине 1 – якорю вибратора. Сам якорь находится между полюсами электромагнита 2, обмотка возбуждения 3 которого питается переменным током от генератора звуковых частот. Кроме того, электромагнит имеет дополнительно обмотку подмагничивания 4, питаемую постоянным током, изменяя величину которого можно управлять амплитудой колебаний якоря, а следовательно, и струны. Амплитуда колебаний струны зависит также и от величины напряжения звуковой частоты, подаваемой с г енератора.

Рисунок 4.

Рисунок 5.

Внимание! Студенты должны иметь ввиду, что если на обмотку подмагничивания напряжение не подается, то якорь, а значит и струна, совершают колебания с удвоенной частотой генератора. К нижнему концу струны прикреплен р ычаг 5, предназначенный для фиксации этого конца струны и регулировки ее натяжения. Ниже точки крепления рычага к струне подвешена платформа 8. Действие веса платформы на струну может быть скомпенсировано весом груза 7, перемещаемого вдоль рычага 5, поворачивающегося вокруг оси 6 в вертикальной плоскости. При балансе сила натяжения струны становится равной нулю ( ). На платформу 8 может быть надето несколько грузов 9 различной массы. Если вес платформы предварительно скомпенсирован, то натяжение струны будет определяться только весом грузов 9. Картину действия сил иллюстрирует рис.5.

Если на предварительно сбалансированную платформу положить груз и включить цепь подмагничивания и звуковой генератор, то от вибратора по струне побегут поперечные волны, которые, периодически отражаясь от концов, образуют сложную картинку колебаний. При медленном изменении частоты звукового генератора можно заметить, что колебания струны упорядочиваются на некоторых частотах – образуются стоячие волны. При этом узлы либо находятся на концах струны, либо делят ее на несколько равных частей. В этом случае говорят, что вдоль струны укладывается одна, две, три и т.д. полуволны. Вращением ручки ЧАСТОТА по и против часовой стрелки можно добиться максимальной амплитуды смещений струны в пучности (настроить установку). Изменение веса груза 9 приводит к исчезновению картины стоячей волны из-за изменения скорости распространения бегущей волны. Однако изменением частоты колебаний звукового генератора можно восстановить стоячую волну с тем же числом узлов на струне.

Порядок выполнения лабораторной работы

Эксперимент 1. Исследование зависимости собственных частот колебаний струны от силы ее натяжения

1. Измерить длину струны линейкой, а ее диаметр микрометром. Взять из таблиц физических величин значение – объемной плотности материала струны. Полученные значения занести в таблицу 1.

Таблица 1

2. Перемещением груза 7 вдоль рычага 5 путем вращения этого груза по или против часовой стрелки добиться компенсации веса пустой платформы 8. При этом, рычаг 5 должен установиться в горизонтальном положении. В качестве критерия баланса используйте положение, при котором груз 7 начнет перевешивать, а струна будет провисать.

3. На обмотку подмагничивания вибратора подайте напряжение постоянного тока, величина которого указывается преподавателем. На передней панели генератора звуковых колебаний установите диапазон частот 20-200 Гц, ручку ЧАСТОТА поставьте в положение 20 Гц, а ручку уровня выходного сигнала поверните по часовой стрелке до упора.

4. На платформу 8 наденьте груз 9 массой не менее 400 г.

5. Включите генератор звуковых частот и дайте ему прогреться в течение 10-15 минут. Медленно увеличивая частоту звукового генератора, получите четкую картину стоячей волны с максимальной амплитудой смещения в пучности сначала для 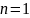, затем для и т.д. (максимальное значение не менее пяти). Записывая каждый раз показания по шкале частот звукового генератора, повторите процесс измерений 3-4 раза, что необходимо для статистической обработки результатов измерений. Результаты занести в таблицу 2.

Таблица 2

В процессе проведения эксперимента следите за выполнением условия (10). Если узлы сильно размыты, уменьшите уровень выходного напряжения генератора звуковых частот.

6. Проделайте аналогичные измерения не менее, чем для пяти различных значений сил натяжения струны. Для этого каждый раз увеличивайте массу груза на 100г. Результаты всех измерений занесите в таблицу 2. Туда же запишите соответствующие значения частот, рассчитанные по формуле
(9).

7. Результаты эксперимента представьте в виде семейства графиков, откладывая по оси абсцисс экспериментальные значения собственной частоты и ее гармоник, а по оси ординат – соответствующие частоты, вычисленные по формуле (9). В качестве параметра возьмите величину силы натяжения струны. Графики стройте с указанием доверительного интервала.

Эксперимент 2. Исследование зависимости скорости распространения волн смещений в струне от силы ее натяжения

1. Пользуясь результатами первого эксперимента, вычислите для каждого значения силы натяжения струны по формуле (8) соответствующие значения скорости распространения волны смещений.

2. По результатам расчета постройте график зависимости с указанием доверительных интервалов.

Характеристики

Список файлов книги