практикум_механика (1) (1106030), страница 24

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 24)

В-третьих, отличие последнего члена в подкоренном выражении (6) от остальных вызвано тем, что период колебаний пустой рамки входит в формулу (5) дважды – в числитель и в знаменатель. Влияние этого члена тем меньше, чем ближе к . Таким образом, массу и радиус эталонного тела нужно выбирать по возможности близкими к массе и размерам исследуемого тела.

В-четвертых, принцип равной точности требует, чтобы все члены под корнем в (6) были одного порядка (за исключением последнего, который может оказаться значительно меньше остальных). Наиболее грубо в этой работе измеряется радиус эталонного шара. Поэтому точность измерения его массы, а также ошибки измерения периодов должны выбираться в соответствии с . Следует иметь в виду, что при измерении времени 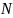колебаний ошибка измерения периода в 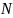раз меньше, чем ошибка секундомера (при выборе этого числа надо руководствоваться принципом равной точности).

Порядок выполнения работы

1. Измерить диаметр эталонного шара (цилиндра) с возможно более высокой точностью и оценить полную среднеквадратичную ошибку этого измерения. Найти массу эталонного шара (цилиндра). Результаты записать в таблицу 1. Вычислить момент инерции по формуле для шара или для цилиндра . Определить относительную ошибку измерения момента инерции по формуле (7).

Таблица 1

2. Провести пробные измерения периодов колебаний , и и выбрать таким образом, чтобы все члены в подкоренном выражении в (6) были не больше, чем . Учитывая, что , выбрать число колебаний, необходимое для обеспечения равной точности.

3. Измерить время соответствующего числа колебаний пустой рамки и найти период . Результаты записать в таблицу 2.

4.С помощью винтов 4 и 5 закрепить в рамке эталонный шар (цилиндр) и найти период колебаний . Результаты записать в таблицу 2.

Таблица 2

5. Закрепить в рамке исследуемый куб и измерить период колебаний . Результаты занести в таблицу 3.

6. Измерить массу куба и длину грани куба. Результаты занести в таблицу 3.

Таблица 3

7. Вычислить момент инерции по формуле (5) и сравнить его с теоретическим значением (см. приложение, формула (14)). Вычислить ошибку.

8. Закрепить в рамке параллелепипед, измерить период колебаний относительно некоторой оси . Результаты записать в таблицу 4.

9. Закрепить в рамке параллелепипед относительно другой оси и измерить период колебаний . Аналогично измерить период колебаний относительно третьей оси . Результаты записать в таблицу 4.

10. Измерить массу параллелепипеда и геометрические размеры. Результаты записать в таблицу 5.

Таблица 4

Таблица 5

11. Вычислить момент инерции по формуле (5) и сравнить с теоретическим значением, вычисленным по формуле (13) (см приложение). Вычислить ошибку.

ПРИЛОЖЕНИЕ

Вычисление моментов инерции симметричных тел

1. Определение момента инерции

Чтобы определить момент инерции тела относительно произвольной оси, разобьем это тело на малые элементы и пронумеруем их. Пусть масса элемента тела с номером «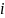 » ( ) равна , а расстояние этого элемента до оси вращения равно . Тогда моментом инерции тела называется предел суммы по всем элементам тела

причем при размеры каждого элемента стремятся к нулю. В математике такой предел называется интегральной суммой, в связи с чем

где определенный интеграл берется по всему объему тела, а обозначает плотность этого тела.

2. Основные свойства момента инерции

• Теорема Штейнера: если есть момент инерции тела относительно произвольной оси, проходящей через его центр инерции, а – его момент инерции относительно другой оси, которая параллельна первой оси и находится на расстоянии от нее, то , где – масса тела.

• Пусть , и обозначают моменты инерции одного и того же тела относительно координатных осей , и . Тогда согласно определению, данному в п.1:

Здесь есть квадрат расстояния элемента до оси (по теореме Пифагора); – его расстояние до оси ; – его расстояние до оси 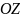; а – расстояние до начала координат. В соответствии с этим

называется «моментом инерции» относительно точки (физического смысла эта величина не имеет).

• Если тело имеет «плоскую» форму, то есть его размеры, например, вдоль оси ничтожно малы по сравнению с размерами вдоль осей и («бесконечно» тонкая пластинка или диск), то

так как , то есть и мы получаем из (9):

, то есть

3. Моменты инерции некоторых тел

Бесконечно тонкий стержень

Рисунок 2.

Р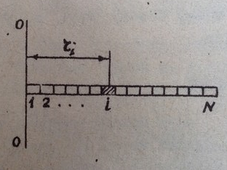 азобьём стержень на 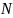равных участков длины 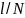, где – длина стержня, – масса стержня, – площадь поперечного сечения, которая считается малой, как показано на рис.2. Масса каждого участка очевидно равна 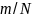. Если ось вращения проходит через конец стержня, то расстояние участка с номером « 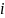» от этой оси равно 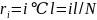. Таким образом, по определению

С помощью полной математической индукции можно проверить, что

так что

Устремляя , легко видеть, что .

Аналогичное вычисление с помощью интегрирования дает тот же результат:

Поскольку центр инерции стержня находится на расстоянии от его конца, то для оси, проходящей через середину стержня, получаем по теореме Штейнера:

Прямоугольный параллелепипед

Рисунок 3.

Н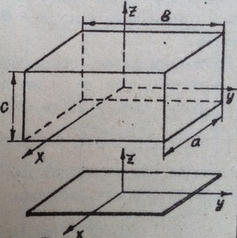 айдем момент инерции относительно оси 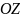(рис.3). Если разрезать мысленно параллелепипед на бесконечно тонкие пластинки, параллельные плоскости 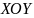, то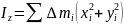

будет для всех таких пластинок одинаковым, так как он не зависит от . Поэтому, если мы найдем для одной такой пластинки, то момент инерции всего тела получится просто путем замены в полученном выражении массы пластинки на массу параллелепипеда.

Рассмотрим поэтому бесконечно тонкую пластинку, перпендикулярную оси 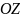(на рис.3 снизу). Для нее можно воспользоваться соотношением (10), согласно которому . Рассматривая , мы видим, что он не зависит от 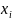, поэтому если разрезать (мысленно) пластинку на «бесконечно тонкие» стержни, параллельные оси , то совпадает с выражением для момента инерции одного такого стержня (длины ), если заменить в нем массу стержня на массу всей пластинки . Аналогично , так что

Аналогично

Если прямоугольный параллелепипед имеет форму куба со стороной

Плоский диск

Чтобы вычислить момент инерции диска (рис.4) относительно оси 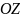, проходящей через центр перпендикулярно его плоскости, разделим его на 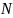колец равной толщины , где – радиус диска. Радиус кольца с номером «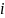 » равен , а его площадь равна

Рисунок 4.

г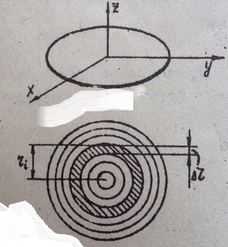 де мы пренебрегли величиной 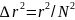по сравнению с 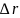, поскольку при она имеет более высокий порядок малости.

Поскольку масса, приходящаяся на единицу площади диска равна , где – масса диска, масса кольца с номером «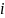 » равна , что с учетом (15) дает

Подставляя эти выражения для и в сумму, определяющую момент инерции, получим:

С помощью индукции легко проверить, что

так что

в пределе при .

Поскольку диск обладает симметрией относительно оси 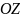, , и используя формулу (10), получим

Тот же результат можно получить с помощью интегрирования:

где обозначает «толщину» диска, а элемент объема равен ( – площадь кольца ширины ).

Цилиндр

Рисунок 5.

П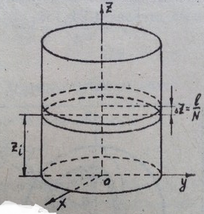 оскольку в выражении 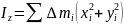не входит , то момент инерции цилиндра относительно этой оси 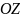выражается тем же соотношением (16)

которое было получено для тонкого диска, если считать в нем равной массе цилиндра. Для того, чтобы убедиться в этом, достаточно разрезать мысленно цилиндр на тонкие диски (толщины ), применить к каждому формулу (16) и сложить полученные выражения с учетом того, что радиусы всех дисков равны и совпадают с радиусом цилиндра (рис.5).

Ввиду симметрии цилиндра , однако формула (10) теперь неприменима, так как цилиндр не является «плоским», а имеет длину .

Чтобы вычислить относительно оси, проходящей через один из концов цилиндра, надо просуммировать выражение (17) для всех дисков толщины , на которые мы разделили цилиндр. Для диска с номером «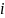 » формула (17) с учетом теоремы Штейнера дает

Характеристики

Список файлов книги