практикум_механика (1) (1106030), страница 27

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 27)

Учитывая, что для всех снарядов используется одна и та же пушка, ответить на вопрос: сообщает ли она всем снарядам одинаковый импульс или одинаковую кинетическую энергию? Ответ подтвердить своим графиком и дать его физическое обоснование.

ЛАБОРАТОРНАЯ РАБОТА 15

ИЗУЧЕНИЕ ЗАКОНОВ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Цель работы: Изучение закона сохранения энергии. Проверка основного закона динамики вращательного движения. Измерение момента инерции твердого тела.

Оборудование: экспериментальная установка с маятником Обербека и электронным секундомером, набор грузов, весы, штангенциркуль.

Краткая теория.

Рисунок 1.

М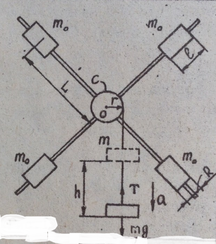 аятник Обербека представляет собой прибор, одно из конструктивных решений которого показано на рис.1. В общем случае это есть некоторое твердое тело, имеющее ось симметрии и способное с малым трением вращаться вокруг этой оси. Принудительное вращение маятника Обербека обеспечивается действием внешней силы, создающей вращательный момент. Эта сила создается действием груза, связанного нерастяжимой и невесомой нитью с вращающимся телом. Величина силы определяется параметрами этого тела и параметрами груза, равноускорено движущегося под действием силы тяжести.

Динамика движения всех тел полностью описывается системой следующих уравнений

где – момент инерции твердого тела относительно его оси вращения; – угловое ускорение вращения твердого тела; – -масса груза; – ускорение поступательного движения груза; 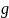– ускорение свободного падения; – сила натяжения нити, создающая вращательный момент ; – плечо силы .

Кинетическая энергия вращения твердого тела определяется выражением

где – угловая скорость вращения.

Следует отметить, что при вращательном движении величина момента инерции тела имеет физический смысл аналогичный массе тела при его поступательном движении, то есть они являются мерой инерции тела.

Определить момент инерции твердого тела можно, записав его как сумму моментов инерции отдельных элементов этого тела

где и – соответственно масса i-го элемента и его расстояние до оси вращения. Однако вычисление момента инерции тела в общем случае представляет довольно сложную задачу, которая относительно легко решается с помощью интегрирования только для тел правильной геометрической формы (симметричных).

В данной лабораторной работе момент инерции вращающегося твердого тела экспериментально определяется двумя способами, сущность которых изложена ниже.

Первый способ. Энергетический подход.

Рассмотрим детальнее устройство маятника Обербека. Прибор состоит из блока 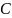радиуса , закрепленного на оси ; четырех одинаковых стержней, расположенных под углом друг к другу и образующих крестовину; четырех одинаковых цилиндрических грузов массы каждый. Эти грузы можно перемещать вдоль стержней и закреплять на заданном расстоянии от оси вращения . Все грузы закрепляются симметрично, то есть так, чтобы центр тяжести всей системы находился в точке .

В некоторой точке окружности блока 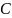на длинной невесомой и нерастяжимой нити прикреплен груз массы . Когда груз свободно висит на нити, не намотанной на блок, он занимает самое низкое положение относительно блока. Будем считать его потенциальную энергию равной нулю в этом положении. Намотав часть нити на блок, мы поднимем груз массы на некоторую высоту относительно нижней точки. При этом он приобретает потенциальную энергию . Если теперь отпустить крестовину, то груз будет опускаться с ускорением . Вращение крестовины будет происходить с угловым ускорением . В процессе движения потенциальная энергия груза будет переходить частично в кинетическую энергию его поступательного движения с линейной скоростью , а частично в кинетическую энергию вращательного движения системы с угловой скоростью . Помимо этого, часть первоначальной потенциальной энергии будет расходоваться на работу преодоления сил трения в оси блока и трения о воздух. В момент, когда груз достигнет нижней точки движения, вся его потенциальная энергия будет израсходована. На основании закона сохранения энергии можем записать

где 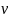– скорость груза массы в нижней точке движения, – угловая скорость крестовины в тот же момент времени. При подготовке эксперимента длину нити регулируют так, чтобы груз массы в начальном положении касался опорной поверхности (стола, пола и т.д.). Тогда во время опыта груз, коснувшись ее, остановится (произойдет неупругий удар) и кинетическая энергия его поступательного движения станет равна нулю. Крестовина, продолжая вращаться по инерции, начнет снова наматывать нить на блок, поднимая груз вверх. Кинетическая энергия крестовины будет расходоваться на увеличение потенциальной энергии груза и на работу по преодолению сил трения. Когда энергия крестовины будет израсходована полностью, груз остановится на высоте . Применяя для этого положения закон сохранения энергии, запишем

где – потенциальная энергия груза, поднятого на высоту , – энергия, равная работе по преодолению сил трения при подъеме груза на высоту . Найдем из (2)

Если не очень сильно отличается от , то расход энергии на работу против сил трения в обоих случаях можно считать одинаковым . Подставим (3) в уравнение (1) и перепишем его относительно момента инерции

Скорость 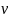груза в нижней точке движения, опустившегося с высоты , можно найти из уравнений движения

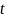Учитывая, что в верхней точке начала движения и измерив и время движения на пути , из (5) получим

Скорость движения груза в любой момент времени совпадает с линейной скоростью точек поверхности блока, на которую наматывается нить (нить считается нерастяжимой). Это позволяет связать ее с угловой скоростью крестовины

где – радиус блока. Учтем (6) в (7) и получим выражение

Подставив (6) и (8) в (4), получим следующее выражение для момента инерции

или, после упрощения,

Поскольку ускорение движения и , то как первый, так и второй члены выражения (9) имеют порядок . Поэтому, пренебрегая единицей и произведя простые алгебраические преобразования, получим окончательно формулу для расчета момента инерции системы

где – диаметр блока, равный .

Второй способ. Динамический подход.

Вращение твердого тела постоянной массы вокруг неподвижной оси описывается уравнением основного закона динамики вращательного движения

где – сумма моментов сил, действующих на тело, – момент инерции тела, – угловое ускорение. Уравнение (11) является прямым следствием второго закона Ньютона и его экспериментальная проверка представляет самостоятельный интерес. В нашем случае его предлагается использовать и для измерения момента инерции маятника Обербека, изображенного на рис.1. Здесь нельзя пренебрегать силами трения, которые создают момент , противодействующий моменту силы натяжения нити. Относительно оси вращения момент силы натяжения нити

Оба момента могут быть сравнимы по величине.

Силу натяжения нити легко найти из уравнения поступательного движения груза массы с ускорением

Величину ускорения найдем из уравнения кинематики равноускоренного движения груза, опускающегося с высоты за время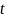

Линейное ускорение связано с угловым ускорением вращения системы условием нерастяжимости нити

Соотношения (12) – (15) позволяют записать уравнение (11) в виде

а входящие в него величины 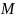и выразить через экспериментально измеряемые величины по формулам

и

При вращательном движении системы, момент сил трения в оси при малых угловых скоростях можно считать постоянным и равным моменту силы трения покоя. Ее величину также предлагается измерить в работе. Постепенно увеличивая массу груза до тех пор пока система не начнет вращаться. Умножив полученное значение массы груза на ускорение свободного падения и на радиус блока, получим искомое значение момента сил трения покоя.

Экспериментальные значения момента инерции системы, полученные расчетом по формулам (10) и (16), необходимо сравнить с расчетной теоретической величиной:

где – момент инерции крестовины (блока со спицами) относительно оси вращения, 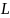– расстояние от центра масс каждого из грузов до оси вращения. Грузы массы имеют форму цилиндров радиуса и длину образующей .

Проверка уравнения (11) основного закона динамики вращательного движения с использованием маятника Обербека тоже может быть осуществлена двумя методами.

Первый метод проверки

Уравнение (11) основного закона динамики вращательного движения можно переписать в виде

Идея метода заключается в следующем. Не меняя положение грузов массы на спицах крестовины, то есть, считая в процессе эксперимента, измерить угловое ускорение вращения системы для нескольких значений момента сил 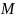натяжения нити. Не имеет значения, каким образом менять величину момента: изменением радиуса блока (взять блок другого радиуса) или изменением силы натяжения нити за счет изменения массы груза, движущегося поступательно вниз. Соотношение (20) должно строго выполняться.

Выразим величины, входящие в (20), через величины, измеряемые экспериментально, считая , и

Характеристики

Список файлов книги