практикум_механика (1) (1106030), страница 26

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 26)

Измерение периода колебаний стержня производится следующим образом:

Нажимаем клавишу СЕТЬ. При этом загораются оба цифровых индикатора на передней панели прибора. Нажимаем клавишу СБРОС. На индикаторах должны высветиться нулевые показания. Это значит, что схема перешла в «ждущий» режим и готова к работе.

После выстрела (или толчка рукой) стержень начинает совершать крутильные колебания. При первом пересечении луча света рычагом 9 автоматически включается секундомер и начинается отсчет времени на индикаторе. На второе пересечение луча света при обратном ходе маятника схема не реагирует. При третьем пересечении луча, когда маятник совершает одно «полное» колебание, на двузначном индикаторе появляется цифра «1». Далее процесс повторяется, так что схема считает все нечетные пересечения луча.

При нажатии клавиши СТОП отсчет времени продолжается только до очередного нечетного пересечения луча света рычагом 9, после чего секундомер автоматически останавливается, а на левом индикаторе высвечивается полное число колебаний 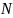за время 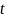, зарегистрированное секундомером. Очевидно, период колебаний равен отношению этих величин .

Методика измерений и оценка их точности

С помощью соотношений (6) и (8) скорость полета снаряда можно вычислить по формуле:

Для этого:

• находим массу тела взвешиванием (до выстрела);

• находим с помощью линейной шкалы, нанесенной на стержне 1 и площадке 6 (после выстрела);

• находим максимальный угол поворота («отброс» маятника) по круговой градусной шкале 8.

Для определения и измеряем периоды собственных колебаний маятника и при двух различных расстояниях и каждого из грузов от оси вращения (центра стержня). При этом по теореме Штейнера

где в входят моменты инерции стержня с площадками 6 и 7 и рычагом 9, а также «собственные» моменты инерции грузов (относительно их центров инерции).

Решая систему уравнений (10) относительно неизвестных и получим:

Если выстрел производится при расстоянии между грузами , то в формуле (9), и подстановка и из (11) окончательно дает:

В соответствии с общим правилом оценки точности косвенных измерений, относительная ошибка измерения скорости этим методом выражается следующей формулой, которая получается дифференцированием выражения (12):

По поводу этой формулы необходимо сделать несколько замечаний. Абсолютная ошибка связана только с округлением числа. Ошибки , , , и содержат все три компоненты (случайную, приборную и ошибку округления) и вычисляются по обычным правилам для прямых измерений.

Ошибки измерения периодов колебаний и могут быть уменьшены (по сравнению с ошибкой секундомера) за счет измерения времени нескольких колебаний. Если число таких колебаний 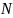, а ошибка измерения времени секундомера равна , то ошибка измерения периода равна . Многократные измерения, как обычно, позволяют уменьшить случайную ошибку. Обратите внимание на отличие последнего члена в формуле (13) от предпоследнего, связанного с тем, что, в отличие от , входит в (12) дважды – в числителе и знаменателе.

Поскольку в знаменателе четырех последних членов в формуле (13) входят разности и , необходимо стремиться, чтобы и как можно больше отличались от и соответственно (при относительное влияние соответствующих ошибок в выражении (13) сильно возрастает). Поэтому надо измерять, когда грузы и почти касаются проволоки (как можно ближе к оси), а в положении, когда они почти касаются площадок 6 и 7 (как можно дальше от оси). При этом разница между и также окажется максимальной. Следует также помнить, что и должны измеряться от центров соответствующих грузов (в соответствии с условием теоремы Штейнера).

Для оценки влияния случайных факторов на величину , можно повторить эксперимент с одним и тем же снарядом и взять среднее значение и среднюю квадратичную ошибку этих измерений. Однако, при этом мы будем измерять, вообще говоря, различные скорости, так как каждый индивидуальный выстрел неповторим. Такие принципиально одноразовые (неповторимые) измерения иногда встречаются в физике; они требуют дополнительного исследования статистических свойств изучаемого явления (например, измерение силы землетрясения содержит случайную ошибку, но ее невозможно определить по разбросу значений, так как это измерение является принципиально однократным).

Условия применимости баллистического метода

Крутильный маятник, используемый в этой работе, можно применять в качестве прибора для измерения моментов сил (он является моделью любого стрелочного прибора с круговой шкалой).

Пусть мы хотим измерить постоянный во времени момент неизвестной силы. Если приложить этот момент к стержню крутильного маятника, то он повернется на угол , который определяется из условия (1):

Произведя калибровку с помощью набора эталонных моментов, можно измерять их в дальнейшем по углу отклонения маятника. При этом, поскольку постоянный момент не изменяется во времени, «период его изменения» следует считать бесконечно большим, то есть , а условие «статического» измерения (14) можно записать в виде:

где – период собственных колебаний маятника.

С другой стороны, при баллистическом измерении, на маятник «действует» момент импульса снаряда в течение короткого времени , удовлетворяющего условию (3), противоположному неравенству (15). При этом угол максимального отклонения (угол отброса), согласно (9), равен

то есть пропорционален моменту импульса 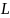. Согласно основному закону динамики вращательного движения, момент сил пропорционален скорости изменения момента импульса :

Но это означает, что с точностью до константы интегрирования:

то есть момент импульса пропорционален интегралу по времени от момента сил.

Поскольку в баллистическом режиме маятник измеряет снаряда, он является прибором для измерения интеграла по времени от момента сил. Для возможности такого механического интегрирования необходимо только, чтобы зависимость приложенного момента сил от времени имела вид кратковременного толчка, соответствующего условию (3).

В заключение необходимо подчеркнуть различие требований к затуханию колебаний при измерении стационарных и импульсных моментов сил.

Для измерения по в соответствии с (14) необходимо, чтобы затухание маятника было большим (критическим), соответствующим режиму апериодического процесса. Иначе стержень, вместо того, чтобы отклониться на угол , будет долго колебаться вокруг этого положения.

С другой стороны, для справедливости формулы (9’) необходимо по возможности малое затухание, так как при выводе этой формулы был использован закон сохранения энергии (7) (мы считали, что кинетическая энергия стержня после удара переходит в упругую энергию нити, закрученной на угол , а потерями энергии на трение пренебрегли). Таким образом, баллистический прибор, помимо условия (3), должен обладать по возможности малым затуханием, в отличие от прибора для измерения постоянных моментов .

Порядок выполнения работы

1. Продумать и составить таблицу для записи результатов измерений.

2. Сдвинув грузы как можно ближе к проволоке (оси вращения), измерить расстояние . Произвести настройку прибора так, чтобы площадка 7 (рис.2) находилась точно напротив нулевого деления шкалы 8, а стержень 9 полностью перекрывал свет от лампочки 10 к фотоприемнику 11.

3.Определить величину логарифмического декремента затухания колебаний. Для этого отклоните маятник на некоторый угол 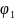и отпустите его. После того, как он совершит 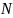полных колебаний (5-10), измерьте его отклонение (в ту же сторону). Логарифмический декремент затухания определите по формуле

Проверьте, удовлетворяет ли он условию . Решите, имеет ли смысл вводить поправки, связанные с . Нужно ли в общую погрешность измерения скорости включить систематическую ошибку, связанную с затуханием. Определите необходимое и достаточное количество полных колебаний.

4. Нажать клавишу СБРОС и убедиться, что на индикаторах высветились нулевые показания. Взвесить тело массы и вложить его в ствол пушки. Взвести пружину, произвести выстрел и измерить амплитуду первого самого большого отброса стержня. Измерить время 5-10 полных колебаний стержня (число колебаний определяется в п.2), для чего нажать клавишу СТОП после появления на двузначном индикаторе цифры «9» (если Вы измеряете 10 полных колебаний). После появления цифры «10» на индикаторе и прекращении отсчета времени вычислить период колебаний , поделив найденное значение времени на число полных колебаний стержня.

5. Остановив маятник, измерить расстояние от проволоки до места попадания снаряда (он должен прилипнуть к пластилину).

6. Сдвинуть грузы массы как можно дальше от центра и измерить расстояние . По методике, описанной в п.3, измерить период колебаний стержня .

7. Вычислить по формуле (12) скорость снаряда 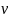. Оценив отдельные члены в формуле (13), выбрать необходимое число колебаний (определяющее точность измерения периодов ) и необходимое число повторений опыта (определяющее точность измерения отброса ), пользуясь принципом равной точности. Значения прилагаются к установке.

8. Повторить измерение необходимое число раз и найти среднее значение скорости и среднеквадратическую ошибку ее измерения.

9. Измерить скорости пяти различных снарядов.

10. Определить зависимость скорости снаряда 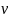от его массы . Для этого, предполагая эту зависимость степенной вида , построить график зависимости от . По углу наклона этого графика определить .

Характеристики

Список файлов книги