практикум_механика (1) (1106030), страница 29

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 29)

2. Наденьте на нить груз массы и зафиксируйте в начальном положении.

3. Проведите измерение времени 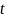движения груза до нижней точки по методике, описанной выше.

4. Измерьте и занесите в таблицу, разработанную самостоятельно, значение величин , , , 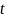и диаметра шкива .

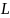5. Повторите измерения еще девять раз для данного значения , и . Результаты занесите в таблицу.

6. Проведите статистическую обработку результатов измерений, определите по формуле (10) среднее значение момента инерции системы и запишите окончательный результат с указанием доверительной вероятности.

Эксперимент 2. Определение момента инерции маятника Обербека (второй способ)

1. Не меняя положения грузов массы относительно оси вращения, увеличивайте величину массы груза , добавляя один за другим грузики, сделанные из листового материала. Найдите такое минимальное значение массы , при котором маятник Обербека начнет вращаться.

2. По формуле определите величину момента сил трения .

3. Укрепив на нити груз массы , произведите измерение времени 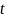его движения с высоты . Повторите измерения для данной массы груза не менее пяти раз.

4. Проведите статистическую обработку результатов и определите по формулам (17) и (18) средние значения момента сил 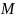натяжения нити и углового ускорения вращения маятника.

5. Повторите этот опыт для 6 – 8 различных значений массы груза. Результаты эксперимента представьте в виде графика, по оси абсцисс которого отложите величину 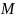, а по оси ординат – угловое ускорение . График постройте с указанием доверительного интервала. По наклону графика определите величину момента инерции маятника Обербека, а по пересечению графика с осью ординат – момент сил трения .

6. Оцените точность результата и запишите окончательное его значение. Сравните величину момента инерции маятника, найденную по результатам первого и второго экспериментов с теоретическим значением, вычисленным по формуле (19), принимая, что в свою очередь

где – масса блока крестовины, и соответственно масса и длина спицы крестовины, – расстояние от центра масс спицы до оси вращения.

7. Укажите возможные причины расхождения результатов, если такие расхождения есть.

Эксперимент 3. Проверка основного закона динамики вращательного движения

1. Задайте постоянные значения массы груза , высоты и диаметра блока .

2. Задайте моменту инерции маятника Обербека серию различных значений, последовательно увеличивая или уменьшая расстояние 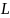центра масс грузов, надетых на спицы крестовины, от оси вращения.

3. Проведите измерение величины времени 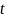движения груза массы на пути для каждого значения момента инерции. Каждое измерение проделайте не менее пяти раз. Проведите статистическую обработку результатов.

4. Подстановкой полученных данных в уравнение (23), убедитесь в справедливости в пределах ошибок измерения этого уравнения, а следовательно, и уравнения (11).

5. Пользуясь результатами эксперимента 2, полученными при условии постоянства момента инерции маятника Обербека, убедитесь в правильности уравнения (21) в пределах ошибок измерения, а следовательно, и уравнения (11).

6. Пользуясь результатами оценки величины момента сил трения , определите относительную ошибку в %, допускаемую при использовании формулы (22) вместо (21), когда мы пренебрегли силами трения. Студентам предлагается самостоятельно найти способ определения этой относительной ошибки.

ЛАБОРАТОРНАЯ РАБОТА 16

ИЗУЧЕНИЕ ЯВЛЕНИЯ РЕЗОНАНСА ПРИ ПОМОЩИ МАЯТНИКА ПОЛЯ

Цель работы: Изучение свободных и вынужденных колебаний механической системы. Измерение основных параметров колебательной системы и снятие ее амплитудных резонансных характеристик.

Оборудование: экспериментальная установка с маятником Поля, электронный секундомер.

Краткая теория.

Особенности колебательного движения механической системы можно рассмотреть на примере движения математического, физического или, в нашем случае, крутильного маятника.

Характер движения определяется как особенностями самой системы, так и действующими на нее силами.

Уравнение движения крутильного маятника можно записать, воспользовавшись основным законом динамики вращательного движения

в виде

Здесь: – момент инерции маятника; – его угловое ускорение; – сумма моментов всех сил, действующих на маятник; – момент упругой или «квазиупругой» силы, возвращающей маятник в положение равновесия; – крутильная постоянная, равная моменту упругих сил, обеспечивающих закручивание маятника на угол в один радиан; – момент сил трения, действующих в системе; – постоянная момента сил трения; – угловая скорость маятника; – момент внешней вынуждающей силы, изменяющейся во времени по гармоническому закону с частотой ; – амплитуда момента внешних сил.

Если внешние силы отсутствуют, то система становится замкнутой, а возникающие в ней колебания называются свободными. Уравнение свободных колебаний имеет более простой вид

Общее решение уравнения (1) имеет вид

Рисунок 1.

П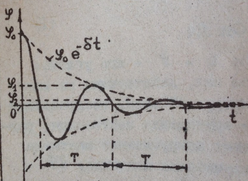 ервый член выражения (3) представляет собой решение однородного уравнения (2), описывающего поведение системы, в которой действуют консервативная упругая возвращающая сила и неконсервативная сила трения. Второй член выражения (3) является частным решение неоднородного уравнения (1) и описывает вынужденные колебания системы.

Рассмотрим особенности колебательного процесса более подробно. Свободные колебания замкнутой системы в общем случае являются затухающими, так как наличие трения в среде приводит к переходу энергии движения маятника в тепло, то есть к рассеянию или диссипации энергии. Вместе с энергией убывает и амплитуда колебаний , как это показано на рис.1.

Математическая запись решения уравнения (2) свободных колебаний имеет вид

где и – начальные амплитуда и фаза колебаний соответственно.

Скорость затухания колебаний определяется коэффициентом затухания , который имеет размерность . От величины коэффициента затухания зависит как круговая частота , так и период свободных колебаний

Время , за которое амплитуда колебаний уменьшается в раз, называют постоянной времени системы. Оно связано с коэффициентом затухания соотношением

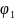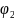Произведение коэффициента затухания на период колебаний , равное логарифму отношения амплитуд и ,соответствующих моментам времени, отличающимся на период

есть величина безразмерная, называемая логарифмическим декрементом затухания .

За время , система успевает совершить колебаний. Учитывая соотношения (6) и (7), получаем

Для характеристики колебательной системы часто употребляется величина , называемая добротностью.

Следует сразу сказать, что как само уравнение (2), так и его решение (4) справедливы, строго говоря, только при условии, что сила трения по величине пропорциональна скорости маятника, а амплитуда колебаний мала. Кроме того, само понятие амплитуды можно сохранить, только, если потери энергии маятником за время одного периода колебаний малы по сравнению с полной энергией колебаний.

Однако, решение вида (4) математически применимо и при значительном затухании. По мере роста частота колебаний уменьшается, а период растет согласно формуле (5). При значениях движение маятника становится апериодическим. Выведенная из состояния равновесия система медленно (без колебаний) возвращается в исходное положение. На рис.2 показаны два возможных способа возвращения системы к положению равновесия в зависимости от величины коэффициента затухания.

П ри незначительном сопротивлении среды, когда потерями в ней можно пренебречь, уравнение (2) приводится к виду

Рисунок 2.

а его решение не содержит больше экспоненциального члена

Амплитуда колебаний уже не уменьшается во времени, а круговая частота и период зависят только от упругих свойств системы и ее момента инерции

Частота называется собственной частотой свободных колебаний системы, а сами колебания – гармоническими.

Все эти соотношения верны только для случая малых колебаний. При больших амплитудах частота и период начинают зависеть от величины амплитуды, а сами колебания перестают быть гармоническими.

До сих пор мы рассматривали свободные колебания системы под действием только внутренних сил. Внешние силы сообщали ей только начальный запас энергии, который либо сохранялся (гармонические колебания), либо расходовался (затухающие колебания). Чтобы исключить затухание колебаний, нужно постоянно возмещать энергию, затрачиваемую на преодоление сил трения. Проще всего этого можно добиться, воздействуя на систему периодической внешней силой, изменяющейся, например, по гармоническому закону. Такая сила называется вынуждающей, а возникшие под ее действием колебания – вынужденными.

В этом случае колебания, рассматриваемого нами крутильного маятника, будут описываться уравнением (1), имеющим решение вида (3). Такие колебания представляют собой суперпозицию свободных затухающих колебаний с частотой и вынужденных колебаний с частотой . Первый член в правой части выражения (3) играет заметную роль только в начале процесса (рис.3). Отрезок времени с момента начала действия вынуждающей силы до момента почти полного затухания свободных колебаний и установления вынужденных называют длительностью переходного процесса. С момента поведение системы практически полностью описывается вторым членом правой части выражения (3)

Рисунок 3.

П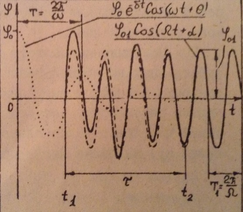 роцесс установления колебаний носит сложный характер и для рассматриваемого крутильного маятника в значительной мере определяется разностью фаз между моментом вынуждающей силы и смещением, скоростью и ускорением маятника. Так, если разность фаз равна , то внешняя сила тормозит маятник и амплитуда его колебаний уменьшается. Если же разность фаз равна нулю (сила совпадает по направлению с вектором скорости маятника), то амплитуда будет увеличиваться. Рост амплитуды прекращается к моменту установления баланса энергии, когда ее потери за счет трения полностью компенсируются притоком энергии извне за счет вынуждающей силы.

Характеристики

Список файлов книги