практикум_механика (1) (1106030), страница 25

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 25)

так как ось (параллельная ), проходящая через центр этого диска, отстоит от оси, проходящей через конец цилиндра, на расстоянии , а в этой формуле обозначает массу диска: .

Используя это выражение, получим:

Для оси, проходящей через центр инерции (через середину цилиндра) получим по теореме Штейнера ( ):

В этом выражении нетрудно узнать сумму выражений (17) для тонкого диска и выражения для момента инерции бесконечно тонкого стержня (12).

Шар

Чтобы вычислить момент инерции шара радиуса и массы относительно оси, проходящей через его центр, разобьём его (мысленно) на 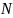тонких сферических слоев одинаковой толщины . Тогда момент инерции шара, показанного на рис.6, будет складываться из моментов инерции этих бесконечно тонких сфер . Пусть масса сферического слоя с номером «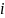 » равна , а его радиус . Поскольку все элементы массы такого слоя отстоят на одинаковое расстояние от центра шара, то для слоя величина , введенная в (9), равна , поскольку (по теореме Пифагора).

П оскольку каждый сферический слой обладает сферической симметрией как и весь шар, для него , так что (9) дает

, то есть

Рисунок 6.

Используя понятие плотности, массу сферы с номером «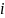 » можно выразить в следующей форме:

Объем сферического слоя равен

где мы оставили только член первого порядка по 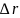(из объема сферы радиуса мы вычли объем «внутренней полости» радиуса ).

Подставляя теперь и , получим:

С помощью индукции можно проверить, что

при . Таким образом, окончательно получаем:

Тот же результат получается при интегрировании в соответствии с (8), если учесть, что (14) дает для элемента объема выражение :

ЗАМЕЧАНИЕ: при применении непосредственно формулы (8) следует иметь в виду, что входящее в нее обозначает расстояние до оси вращения (в цилиндрической системе координат), в то время как интегрирование в последнем выражении производилось вдоль радиуса сферы (то есть в сферической системе координат). Это объясняет появление множителя , который появляется за счет интегрирования по полярному углу в сферической системе координат.

4. Расчет положения центра тяжести полуцилиндра

Рисунок 7.

Р ассмотрим полуцилиндр массы 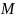и радиуса (рис.7). Обозначим расстояние от его диаметра до центра инерции через . По определению центра инерции

где – масса узкой полоски шириной , заштрихованной на рис.7. Высота заштрихованной полоски связана с ее расстоянием от начала координат и радиусом полуцилиндра теоремой Пифагора:

Обозначив массу на единицу площади через , получим

Подставляя это выражение в (22), и сокращая 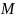, получим:

Делая замену переменных , и вычисляя интеграл, получим окончательно:

ЛАБОРАТОРНАЯ РАБОТА 14

ИЗМЕРЕНИЕ СКОРОСТИ ПОЛЕТА ТЕЛА МЕТОДОМ КРУТИЛЬНОГО БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Цель работы: Экспериментальное изучение законов сохранения. Ознакомление с баллистическим режимом движения колебательной системы. Измерение скорости быстро летящего тела.

Оборудование: экспериментальная установка с крутильным баллистическим маятником, электронным секундомером и набором тел различной массы, весы, штангенциркуль.

Краткая теория.

Пусть вертикально натянутая упругая нить (проволока) проходит через центр тяжести горизонтально расположенного стержня, так что его вес уравновешен разностью натяжений на верхнем и нижнем участках нити. При повороте стержня на малый угол вокруг вертикальной оси, совпадающей с проволокой, на него будет действовать возвращающий момент упругих сил 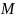, равный по закону Гука

где – модуль кручения нити.

Поскольку нить неподвижна, уравнение движения стержня описывает его вращение вокруг неподвижной вертикальной оси и имеет вид:

где – момент инерции стержня, – его угловое ускорение.

Это есть уравнение гармонических колебаний системы, которая называется крутильным маятником. Период этих колебаний .

Пусть некоторое тело массы m, летящее горизонтально (по инерции) со скоростью , ударяется о стержень на расстоянии от оси вращения (проволоки) и застревает в нем. Как будет двигаться после этого стержень с застрявшим в нем телом?

Рисунок 1.

Рассмотрим подробнее момент удара и последующее движение системы. На рис.1 ось вращения перпендикулярна плоскости рисунка, и вектор скорости тела в момент удара для п ростоты считаем перпендикулярным стержню. Поскольку тело застревает в стержне, они после удара движутся вместе, то есть удар является абсолютно неупругим, так что кинетическая энергия тела массы частично переходит во внутреннюю энергию и тратится на работу неупругой деформации (механическая энергия не сохраняется). Если тело массы движется достаточно быстро, то время удара будет значительно меньше периода собственных колебаний маятника , соответствующего уравнению (2), то есть

При этом говорят, что маятник движется в баллистическом режиме (под воздействием кратковременного толчка), или просто называют его «баллистическим». Условие (3) позволяет пренебречь смещением стержня за время удара и применить законы сохранения, считая .

Если – масса стержня и – скорость движения системы как целого непосредственно после удара, то закон сохранения импульса имеет вид:

где – сила «реакции оси», приложенная к стержню со стороны нити. Натянутая нить (проволока) не позволяет стержню двигаться поступательно, поэтому . Из уравнения (4) видно, что и при должно быть (такой результат получился от того, что мы пренебрегли деформацией изгиба нити, учет которой дал бы конечную величину). Таким образом, импульс тела «поглощается» в кронштейнах, между которыми натянута нить, так что система является незамкнутой (по отношению к сохранению импульса).

С другой стороны, закон сохранения момента импульса дает:

где – угловая скорость вращения системы непосредственно после удара, 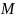– момент упругих сил (1) и тело массой считается точечным (с моментом инерции ).

При , остается конечной величиной, а правая часть (5) стремится к нулю. Поэтому уравнение (5) позволяет выразить скорость движения тела массой (до удара):

где в числителе мы пренебрегли величиной по сравнению с из-за ее малости.

Поскольку и можно измерить непосредственно, для определения скорости полета тела 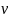нам необходимо найти и .

После удара маятник приходит во вращение с угловой скоростью , и, поворачиваясь, он закручивает нить. В результате кинетическая энергия его вращательного движения переходит в энергию упругой деформации нити

где – максимальный угол поворота (при изменении от 0 до , угловая скорость вращения изменяется от до 0). Таким образом

и задача нахождения скорости 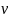сводится к определению и , которые могут быть найдены по измеренному периоду собственных колебаний маятника.

Описание экспериментальной установки

Установка с крутильным баллистическим маятником (рис.2) состоит из стержня 1, растянутого на двух вертикальных проволоках 2, прикрепленных к верхнему 3 и нижнему 4 кронштейнам вертикального штатива. На концах стержня имеются две площадки: площадка 6, покрытая пластилином для неупругого удара тела («снаряда»), и площадка 7 с вертикальной риской на торце, используемой для отсчета углов поворота стержня по градусной шкале 8. Вдоль стержня могут перемещаться два груза массы каждый, расположенные симметрично относительно оси подвеса. Эти грузы закрепляются с помощью винтов на одинаковых расстояниях от оси вращения. Расстояния измеряются с помощью делений, нанесенных на стержне 1.

Рисунок 2.

П осередине стержня 1 прикреплен изогнутый рычаг 9, который при колебаниях стержня служит для прерывания света, падающего от лампочки 10 на фотоприемник 11. Фотоприемник соединен с электрическим секундомером 12 и служит для его автоматического включения и выключения.

На лицевую панель электронного секундомера 12, закрепленного вместе со штативом 5 на основании 13, выведены клавиши управления СЕТЬ, СБРОС, СТОП и индикаторы: двузначный для отсчета числа полных колебаний стержня 1 и пятизначный – для отсчета времени колебаний. Кроме того, в установке имеется пружинная «пушка» 14 и набор «снарядов» различной массы, скорости которых после «выстрела» измеряются в этой работе.

Характеристики

Список файлов книги