20 Матрицы Адамара (1044281)
Текст из файла
3
Лекция 20. Строение матрицы Адамара
Элементы матрицы  можно вычислить непосредственно. Нумерацию строк и столбцов начнем с 0. В этом случае номер строки или столбца задается двоичным вектором:
можно вычислить непосредственно. Нумерацию строк и столбцов начнем с 0. В этом случае номер строки или столбца задается двоичным вектором: 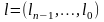 . Положим
. Положим  .
.
Предложение. Элемент матрицы  .
.
Доказательство. Для  утверждение очевидно. Рассмотрим
утверждение очевидно. Рассмотрим  , где каждый блок есть матрица Адамара меньшего порядка. Если элемент находится в блоке
, где каждый блок есть матрица Адамара меньшего порядка. Если элемент находится в блоке  , то
, то  и по предположению индукции формула верна. Если элемент находится в блоке
и по предположению индукции формула верна. Если элемент находится в блоке  , то
, то  . Однако
. Однако  . Если же элемент находится в блоке
. Если же элемент находится в блоке  , то
, то  и
и  .
.
Данное предложение позволяет при работе с матрицами высокого порядка генерировать элементы матрицы, а не хранить их в памяти.
Код Грея.
Ниже будет показана связь матриц Адамара со специальным способом кодирования целых чисел. Выберем натуральное 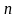 и выпишем в виде таблицы двоичные представления всех чисел от 0 до
и выпишем в виде таблицы двоичные представления всех чисел от 0 до  . Например, для
. Например, для 
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |

Обратим внимание на два обстоятельства. Таблица обладает симметрией, которую можно описать следующим образом. Таблица для
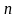 состоит из двух экземпляров таблицы для
состоит из двух экземпляров таблицы для 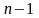 , что подчеркнуто наличием стрелок , при этом в первом экземпляре добавлена нулевая строка, а во втором - единичная. Другой момент заключается в том, что соседние столбцы могут различаться более чем в одном разряде. Последнее обстоятельство препятствует использованию данной кодировки в асинхронных цифровых схемах. В этой связи возникла задача придумать такую кодировку целых чисел, чтобы два стоящих рядом числа различались лишь в одной позиции. Наиболее популярной является кодировка под названием код Грея. Если число имеет двоичное представление
, что подчеркнуто наличием стрелок , при этом в первом экземпляре добавлена нулевая строка, а во втором - единичная. Другой момент заключается в том, что соседние столбцы могут различаться более чем в одном разряде. Последнее обстоятельство препятствует использованию данной кодировки в асинхронных цифровых схемах. В этой связи возникла задача придумать такую кодировку целых чисел, чтобы два стоящих рядом числа различались лишь в одной позиции. Наиболее популярной является кодировка под названием код Грея. Если число имеет двоичное представление 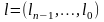 , то код Грея для него имеет вид
, то код Грея для него имеет вид 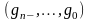 , где
, где 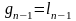 , а
, а 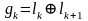 ,
, 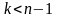 , а знак
, а знак 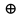 означает суммирование по модулю 2.
означает суммирование по модулю 2.Предложение. В коде Грея коды соседних чисел различаются лишь в одном разряде.
Доказательство. Рассмотрим двоичные представления двух соседних чисел: 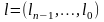 и
и  .
.  . Число
. Число  , где серия из единиц может быть и пустой, но 0 обязательно присутствует. В этом случае
, где серия из единиц может быть и пустой, но 0 обязательно присутствует. В этом случае  (серия из 1 заменилась серией той же длины из 0, а 0 заменился на 1). Сравнивая коды Грея обоих чисел, убедимся, что они различаются лишь в одной позиции.
(серия из 1 заменилась серией той же длины из 0, а 0 заменился на 1). Сравнивая коды Грея обоих чисел, убедимся, что они различаются лишь в одной позиции.
Переход от обычного кода к коду Грея и обратно можно выразить с помощью линейного преобразования над полем  :
:  , а
, а  . У этой матрицы есть обратная
. У этой матрицы есть обратная  .
.


Последовательные числа, закодированные кодом Грея, также обладают определенной симметрией: таблица для
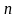 представляется в виде, указанном на рисунке. При этом направление стрелок означает зеркальную симметрию соответствующих частей кода Докажем это. Для
представляется в виде, указанном на рисунке. При этом направление стрелок означает зеркальную симметрию соответствующих частей кода Докажем это. Для 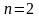 справедливость проверяется непосредственно. Таблицу закодированных чисел, используя выражения для
справедливость проверяется непосредственно. Таблицу закодированных чисел, используя выражения для 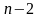 , представим в виде, представленном на рисунке. Используя предположении индукции и правило построения кода, получим
, представим в виде, представленном на рисунке. Используя предположении индукции и правило построения кода, получим Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.














