2 Преобразование Фурье и обобщенные функции (1044232)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

4

Лекция 2. Преобразование Фурье и обобщенные функции

Вспомогательные утверждения

Лемма. Справедлива формула

(1)

Доказательство. Хотя формула (1) хорошо известна, мы приведем ее доказательство, поскольку она является основой многих дальнейших выкладок. Рассмотрим контур, изображенный на рис.1

Рис. 1. Контур интегрирования

и интеграл по контуру в указанном направлении от аналитической функции 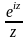. Имеем 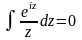, поскольку у функции нет особенностей внутри области интегрирования. Здесь контур 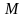- дуга окружности радиуса 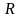, а контур 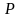- дуга окружности радиуса 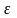. Обе дуги имеют центр в начале координат. За исключением крайних точек, на контуре 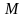выполнено неравенство 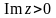, поэтому с ростом 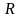интеграл по этому контуру стремится к 0. Интегралы по контурам 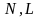в сумме дают 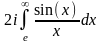. Найдем теперь интеграл по контуру 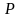. Сделаем замену 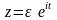. В результате интеграл по этому контуру примет вид 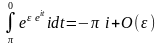. Последняя оценка получена в результате разложения подынтегральной функции в ряд. Устремляя 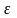к 0, завершаем доказательство.

Следствие 1.

при любом .

Доказательство проводится путем замены переменной

Следствие 2

.

Для любого

Доказательство. . Второе слагаемое стремится к 0 когда .

Из соображений симметрии вытекает формула

(2)

Пример отыскания обобщенных функций

Под обобщенной функцией понимается непрерывный функционал. Примером такой функции является -функция.

Предложение 1. .

Доказательство. Очевидно, что обычное преобразование Фурье от 1 не существует. Положим . Не существует обычного предела у этой функции при . Найдем функционал . Если 0 не попадает в интервал интегрирования, подынтегральная функция не имеет особенностей, и весь интеграл стремится к 0. В противном случае, интеграл стремится к , где произвольное малое положительное число. Второе слагаемое исчезает в силу симметричности, и при получаем, используя (2), конечный результат.

Следствие 3. . Доказательство. Формально утверждение есть следствие общего правила: , но фактически надо доказать, что это правило распространяется и на обобщенные функции. Проще всего, дать прямое доказательство.

Производные от обобщенных функций

Производная определяется путем формального применения интегрирования по частям с учетом компактности носителя функций из : . В качестве примера рассмотрим обобщенную функцию , заданную равенством: и найдем производную от нее. Имеем . Это означает, что .

Замечание. Следует быть очень осторожным применяя к обобщенным функциям формулы, связывающие производную от функции и ее преобразование Фурье. В качестве примера рассмотрим отыскание преобразование Фурье от . Действуя формально, можем получить: , откуда . Теперь, исходя из определения, найдем правильный ответ. Положим и подсчитаем . Если точка 0 не входит в интервал интегрирования, то интеграл стремится к , то есть ожидаемый результат. Если же точка 0 принадлежит интервалу интегрирования, то наряду с указанным слагаемым появится еще одно.

Второе слагаемое исчезает в силу симметрии, а из третьего слагаемого получаем -функцию. Окончательный результат выглядит так: . Отметим, что отсюда получается правильный результат для преобразования Фурье от функции, поскольку .

Замечание. Интеграл существует в смысле главного значения для функции из . Это означает существование соответствующего функционала.

Задача 2. Дать строгое доказательство утверждения

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов лекций