Измеримые пространства
§ 2. Измеримые пространства.
Примеры  -алгебр:
-алгебр:
1)  =(0,
=(0,  ) – бедная
) – бедная  алгебра,
алгебра,
2)  ={A:A
={A:A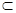
 } - богатая
} - богатая  алгебра,
алгебра,
3)  ={A:, A, 0,
={A:, A, 0, } называют алгеброй, порожденной множеством А.
} называют алгеброй, порожденной множеством А.
Вопрос: Когда алгебра А( ) будет являться
) будет являться  алгеброй F?
алгеброй F?
Определение . Система М( ) подмножеств
) подмножеств  называется монотонным классом, если из того, что А
называется монотонным классом, если из того, что А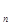
 М(
М( ) n=1,2,.. и
) n=1,2,.. и  , т.е.
, т.е.  и
и  следует, что
следует, что  М(
М( ).
).
Теорема 2. Для того, чтобы алгебра А( ) была
) была  алгеброй F необходимо и достаточно, чтобы она являлась монотонным классом.
алгеброй F необходимо и достаточно, чтобы она являлась монотонным классом.
Рекомендуемые материалы
2.1. Измеримое пространство (R1, B (R1))
Пусть R1=(- ,
, ] – действительная прямая и (a,b] = {
] – действительная прямая и (a,b] = { R1:
R1:  } для всех
} для всех  . Обозначим через А(R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b] :
. Обозначим через А(R1) систему множеств в R1, состоящую из конечных сумм непересекающих интервалов вида (a,b] :  А(R1), где
А(R1), где  . Нетрудно видеть, что эта система множеств, а также
. Нетрудно видеть, что эта система множеств, а также  – образуют алгебру – А(R1) , которая не является
– образуют алгебру – А(R1) , которая не является  алгеброй, так как
алгеброй, так как  А(R1), но
А(R1), но  А(R1).
А(R1).
Определение. B (R1) – наименьшая  алгебра, порожденная А(R1) называется борелевской
алгебра, порожденная А(R1) называется борелевской  алгеброй, а ее множества – борелевскими.
алгеброй, а ее множества – борелевскими.
Если обозначить через  систему интервалов (a,b], а через
систему интервалов (a,b], а через  - наименьшую
- наименьшую  алгебру содержащую
алгебру содержащую  . Нетрудно установить B (R1)=
. Нетрудно установить B (R1)=  .
.
Из каких элементов B (R1)? Из предыдущих построений следует, что B (R1) состоит из интервалов вида  , где
, где  , и их счетных объединений и пересечений. Отсюда следует, что:
, и их счетных объединений и пересечений. Отсюда следует, что:
i)  ii)
ii) iii)
iii)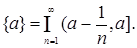
2.2. Измеримое пространство (Rn,B (Rn))
Пусть Rn = R R
R …
… R – называется прямое или декартово произведение n экземпляров числовой прямой, то есть, множество упорядоченных наборов
R – называется прямое или декартово произведение n экземпляров числовой прямой, то есть, множество упорядоченных наборов  , где
, где  ,
,  .
.
Множество  где
где  , называется прямоугольником, то есть,
, называется прямоугольником, то есть,  Rn :
Rn : , а
, а  - его сторонами.
- его сторонами.
Через  (Rn) обозначим совокупность всех прямоугольников из Rn.
(Rn) обозначим совокупность всех прямоугольников из Rn.  (Rn) - наименьшая
(Rn) - наименьшая  алгебра порожденная
алгебра порожденная  - называется борелевской
- называется борелевской  алгеброй множеств Rn, которую и обозначим через B (Rn).
алгеброй множеств Rn, которую и обозначим через B (Rn).
2.3. Измеримое пространство (R ,B (R
,B (R ))
))
R - пространство числовых последовательностей
- пространство числовых последовательностей  где -
где -  ,
,  Пусть
Пусть  - борелевское множество к-ой числовой прямой (то есть, множество
- борелевское множество к-ой числовой прямой (то есть, множество  B (R1)). Рассмотрим множества :
B (R1)). Рассмотрим множества :
i)  R
R  :
: };
};
ii)  R
R  :
: };
};
iii)  B (R
B (R  )
)  R
R  :
:  .
.
Такие множества называются цилиндрическими, причем  называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества
называют основанием цилиндра, а остальные координаты – образующими цилиндра. Нетрудно видеть, что множества  ,
,  ,
,  образуют алгебру. Обозначим наименьшие
образуют алгебру. Обозначим наименьшие  алгебры, порожденные множествами вида i)-iii) через B (R
алгебры, порожденные множествами вида i)-iii) через B (R ), B1(R
), B1(R ), B2(R
), B2(R ), соответственно. Можно показать, что эти
), соответственно. Можно показать, что эти  алгебры совпадают.
алгебры совпадают.
2.4. Измеримое пространство (RТ , B (RТ))
Пусть Т – произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные
– произвольное пространство, множество. Пространство RТ – совокупность действительных функций на T со значениями в R1, обозначенные  . Для простоты будем считать, что
. Для простоты будем считать, что  . Обозначим:
. Обозначим: , где
, где  . Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить
. Проводя рассуждения аналогичные приведенным в пункте 2.3, легко построить  алгебру борелевских множеств на RТ, порожденную цилиндрическими множествами
алгебру борелевских множеств на RТ, порожденную цилиндрическими множествами  и обозначаемую через B (RТ).
и обозначаемую через B (RТ).
Возникает вопрос: какова структура множества  B (RТ)? Оказывается, что любое множество
B (RТ)? Оказывается, что любое множество  B (RТ) допускает представление
B (RТ) допускает представление  , где
, где  B (R
B (R ). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t
). Отсюда следует, что множества, зависящие от поведения функций в несчетном числе точек t  Т необязаны быть измеримыми относительно B (RТ). Например: i)
Т необязаны быть измеримыми относительно B (RТ). Например: i)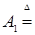
 },
}, 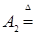
 ,
,
ii)
 - непрерывные в точке
- непрерывные в точке  .
.
В связи с неизмеримостью некоторых множеств из RТ по отношению к B (RТ) естественно рассматривать более узкие функциональные пространства.
2.5. Измеримое пространство (С[0,T], B (С[0,T])).
Сердечно-сосудистая система - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Пусть Т=[0,1], С[0,1] - пространство непрерывных функций xt, t [0,1], со значениями в R1. Очевидно, С[0,1] –метрическое пространство, относительно метрики ρ(х,у)=
[0,1], со значениями в R1. Очевидно, С[0,1] –метрическое пространство, относительно метрики ρ(х,у)= 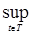
 , то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами:
, то есть ρ(х,у) – расстояние между двумя непрерывными функциями, обладающие свойствами:
1) ρ (х,у)=0 x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у)
x=y; 2) ρ (х,у)= ρ (у,x); 3) ρ (х,у) ρ (x,z)+ ρ(z,y).
ρ (x,z)+ ρ(z,y).
Через B (С[0,T]) обозначим наименьшую  алгебру, порожденную цилиндрическими множествами, которые строятся аналогично пункту 2.4.
алгебру, порожденную цилиндрическими множествами, которые строятся аналогично пункту 2.4.
2.6. Измеримое пространство (D,B(D)).
D – пространство функций xt , t  [0,1], со значениями в R1 , непрерывные справа, имеющие пределы слева в любой точке t
[0,1], со значениями в R1 , непрерывные справа, имеющие пределы слева в любой точке t [0,1]. В нем также можно ввести метрику:
[0,1]. В нем также можно ввести метрику:
ρs(x,y) inf {
inf { ,
,
где  - множество строго возрастающих непрерывных на отрезке [0,1] функций
- множество строго возрастающих непрерывных на отрезке [0,1] функций  , причем
, причем  и
и  }.
}.  -алгебра B(D) строится аналогично пункту 2.4.
-алгебра B(D) строится аналогично пункту 2.4.


















