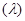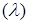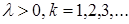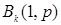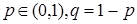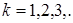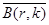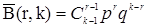Задание вероятностных мер на измеримых пространствах
§ 3. Задание вероятностных мер на измеримых пространствах.
3.1. Измеримое пространство (R1,B(R1)).
Пусть F: R1 [0,1] - измеримая функция, обладающая свойствами:
[0,1] - измеримая функция, обладающая свойствами:
1) неубывающая;
2) F(- )=0 F(
)=0 F( )=1, где F(-
)=1, где F(- )=
)= и F(
и F( )=
)= ;
;
3) непрерывна справа и имеет предел слева в каждой точке  R1.
R1.
Определение. Всякая функция F(x), удовлетворяющая свойствам 1)- 3) называется функцией распределения на R1 .
Теорема 3. Пусть  - функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых
- функция распределения на R1, тогда на (R1, B(R1)) существует и притом единственная вероятностная мера Р такая, что для любых  , причем
, причем  , Р
, Р
Пример: пусть функция распределения  имеет вид:
имеет вид:
Рекомендуемые материалы
 =
=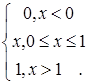
Соответствующую ей меру называют мерой Лебега отрезка  и обозначают Λ, причем Λ
и обозначают Λ, причем Λ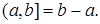
Приведем классификацию мер на (R1, B (R1)).
3.1.1. Дискретные меры.
Пусть  - функция распределения кусочно-постоянна и меняет свои значения в точках
- функция распределения кусочно-постоянна и меняет свои значения в точках  х1,х2, …, причем
х1,х2, …, причем  где
где  Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р
Ясно, что соответствующая этой функции распределения вероятностная мера Р сосредоточена в точках х1,х2, …, причем Р
 .
.
Набор чисел  где
где  - называется дискретным распределением.
- называется дискретным распределением.
Примеры дискретных распределений содержатся в приведенной ниже таблице.
| Распределение |
| Параметры |
| 1. Дискретное равномерное |
|
|
| 2. Бернулли |
|
|
| 3. Биноминальное |
|
|
| 4. Пуассоновское Пк | Пk |
|
| 5. Геометрическое = |
|
|
| 6. Отрицательное биноминальное |
|
|
3.1.2. Абсолютно непрерывные меры.
Пусть существует неотрицательная функция 
 такая, что функция распределения
такая, что функция распределения  допускает представление:
допускает представление: 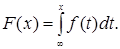
Функцию 
 (
( ) называют плотностью функции распределения
) называют плотностью функции распределения  .
.
Пример: Функцию  ,
,  называют гауссовской плотностью. Легко убедиться в том, что
называют гауссовской плотностью. Легко убедиться в том, что 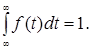
3.1.3. Сингулярные распределения.
Определение. Точка  называется точкой роста функции распределения
называется точкой роста функции распределения , если
, если  для любого
для любого  .
.
Определение. Сингулярными мерами называются меры, функции распределения которых непрерывны, причем точки роста, которые образуют множество нулевой меры Лебега.
Пример. Возьмем отрезок  и построим на нем сингулярную функцию распределения
и построим на нем сингулярную функцию распределения  с помощью приема, принадлежащего Кантору Г. Пусть Fo – функция распределения, соответствующая мере Лебега на отрезке [0,1].Разделим
с помощью приема, принадлежащего Кантору Г. Пусть Fo – функция распределения, соответствующая мере Лебега на отрезке [0,1].Разделим  на 3 равные части и определим - функцию распределения
на 3 равные части и определим - функцию распределения следующим образом:
следующим образом:
 = 0, при x < 0;
= 0, при x < 0;  =
=  x, при x
x, при x  [0,
[0, );
);  =
=  , при x
, при x  [
[ ,
, );
);  =
=  x –
x –  , при x
, при x  [
[ ,1);
,1);  = 1, при x > 1. Затем, каждый из интервалов
= 1, при x > 1. Затем, каждый из интервалов  и
и  опять поделим на 3 равные части и определим функцию распределения
опять поделим на 3 равные части и определим функцию распределения  следующим образом:
следующим образом:
 = 0, при x < 0;
= 0, при x < 0;  =
=  x, при x
x, при x  [0,
[0, );
);  =
=  при x
при x [
[ ,
, ];
]; =
=  x -
x -  , при x
, при x [
[ ,
, ];
]; =
=  при x
при x [
[ ,
, );
); =
=  x – 1, при x
x – 1, при x [
[ ,
, );
); =
=  при x
при x [
[ ,
, );
); =
=  x -
x -  , при x
, при x [
[ ,1].
,1].
Продолжая этот процесс далее мы построим последовательность функции распределения  , которая, очевидно, сходится при
, которая, очевидно, сходится при  к некоторой неубывающей непрерывной функции распределения
к некоторой неубывающей непрерывной функции распределения  . Очевидно, что точки роста функции распределения
. Очевидно, что точки роста функции распределения имеет нулевую меру Лебега, так как общая длина интервалов, на которых
имеет нулевую меру Лебега, так как общая длина интервалов, на которых  принимает постоянные значения равна 1. Действительно, общая длина интервалов постоянства функции
принимает постоянные значения равна 1. Действительно, общая длина интервалов постоянства функции  равна
равна 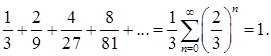
Пусть  - множество точек роста функции распределения
- множество точек роста функции распределения , тогда из последнего рассуждения следует, что
, тогда из последнего рассуждения следует, что  (в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега
(в этих случаях говорят, что мера, соответствующая этой функции распределения сингулярна по отношению к мере Лебега  ).
).
Теорема 4.(Лебега) Любая функции распределения на прямой R1 представима в виде:
на прямой R1 представима в виде:
 ,
,
где  и
и  , а
, а  - дискретная,
- дискретная,  - абсолютно непрерывная,
- абсолютно непрерывная,  - сингулярная функции распределения.
- сингулярная функции распределения.
3.2. Измеримое пространство (Rn ,B(Rn)).
Пусть  - измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор
- измеримая функция, непрерывная справа (по совокупности измененных), имеющая левый предел. Введем оператор 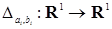
 , действующей по правилу
, действующей по правилу
 .
.
Определение. Всякая непрерывная справа функция  удовлетворяющая условиям:
удовлетворяющая условиям:
1)  для любых
для любых  , i =
, i =  ;
;
2)  ;
;
3)  , если хотя бы одна из координат n-мерного вектора
, если хотя бы одна из координат n-мерного вектора  принимает значение
принимает значение  ,
,
называется  -мерной функцией распределения.
-мерной функцией распределения.
Очевидно следующее утверждение.
Теорема 5. Пусть  -
-  -мерная функция распределения. Тогда на (Rn,B(Rn)) существует единственная вероятностная мера Р такая, что
-мерная функция распределения. Тогда на (Rn,B(Rn)) существует единственная вероятностная мера Р такая, что  , где
, где  ,
,  .
.
Примеры. 1) Пусть
 =
=
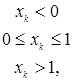
 мерная функция распределения вероятностей, которой соответствует мера Лебега на
мерная функция распределения вероятностей, которой соответствует мера Лебега на  .
.
2)  ,где
,где
 .
.
3.3. Измеримое пространство (R ,B(R
,B(R ))
))
Обозначим через  R
R :(
:( )
) , где
, где  Rn – цилиндрическое множество в
Rn – цилиндрическое множество в  с основанием
с основанием  B(Rn). Пусть последовательность вероятностных мер
B(Rn). Пусть последовательность вероятностных мер  определенных, соответственно, на (R1 , B(R1)), (R2 , B(R2)), обладает следующим свойством:
определенных, соответственно, на (R1 , B(R1)), (R2 , B(R2)), обладает следующим свойством:
 (1)
(1)
где  ,
,  .
.
Условие (1) называют условием (свойством) согласованности.
Теорема 5. (Колмогорова о продолжении вероятностной меры на (R , B(R
, B(R )). Пусть
)). Пусть  - последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R
- последовательность вероятностных мер, соответственно, на (R1, B(R1)), (R2, B(R2)), обладающая свойством согласованности. Тогда существует единственная мера Р на (R , B(R
, B(R )) такая, что для каждого
)) такая, что для каждого  P
P P
P для
для  .
.
3.4. Измеримое пространство (RТ , B(RТ))
Обратите внимание на лекцию "Движение ледников".
Пусть Т=[0,T] – произвольное множество индексов
– произвольное множество индексов  Rt - числовая прямая, соответствующая индексу
Rt - числовая прямая, соответствующая индексу  . Рассмотрим произвольный конечный неупорядоченный набор
. Рассмотрим произвольный конечный неупорядоченный набор  различных индексов
различных индексов  , и пусть Pt - вероятностная мера на (R
, и пусть Pt - вероятностная мера на (R ,B(R
,B(R )), где R
)), где R = R
= R R
R .
.
Определение. Будем говорить, что семейство вероятностных мер  (
( - пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов
- пробегает множество всех конечных неупорядоченных наборов), является согласованным, если а) для любых двух наборов  и
и  причем
причем  , выполняется равенство
, выполняется равенство
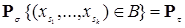
 ,
,
где  , б) выполнено (1).
, б) выполнено (1).
Теорема 6. (Колмогорова о продолжении вероятностной меры на
(RТ ,B(RТ))). Пусть  - согласованное семейство вероятностных мер на (R
- согласованное семейство вероятностных мер на (R ,B(R
,B(R )). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что
)). Тогда существует единственная вероятностная мера Р на (RТ ,B(RТ)) такая, что  для всех неупорядоченных наборов
для всех неупорядоченных наборов  различных индексов
различных индексов  и
и  B(R
B(R ).
).



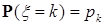
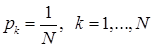
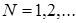
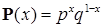

 - вероятность успеха,
- вероятность успеха, 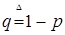
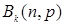
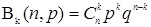

 ,
,