[5] Сверхпроводники (987503), страница 4

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 4)

Д

иамагнитное описание сверхпроводника позволяет ис­пользовать обычные формулы для магнитного поля в образ­цах различной формы с учетом фактора размагничивания N:

(5.2.22)

Для однородного эллипсоида вектора В, Н и J постоянны и параллельны внешнему полю, и соотношение (5.2.22) записывается в скалярной форме Н_i=Н_e-NJ, где

N={1/e²-1)*(1/(2e)*ln[(1+e)/(1-a)]-1}, где e=(1-b²/a²)^1/2,

a и b большая и малая полуоси эллипсоида. Для бесконечного цилиндра с осью, параллельной полю, N =0; для бесконеч­ного цилиндра с осью, перпендикулярной полю, N=1/2; для сферы N=1/3.

Р
ис. 5.2.10. а—кривые намагничивания образца, имеющего форму стержня; б — магнитное поле внутри образца; 1— в продольном пиле (N~0); 2 — в поперечном поле (N~1/2); 3 — образец в форме шара (N=1/3)

На рис.5.2.10 приведены зависимости намагниченности J и B_i от напряженности внешнего поля H_e для СП, имеющего форму цилиндра с осью, параллельной H_e (N = 0). При уве­личении Н_е В_i=0, пока H_e не достигнет некоторого критиче­ского значения H_с, после чего СП переходит в нормальное состояние, т.е. сверхпроводимость разрушается магнитным полем (кривая 1). Кривые 2 и 3 соответствуют зависимости В_i от Н_е для цилиндра в поперечном поле (N=1/2) и для сферы (N = 1/3). Итак, эффект выталкивания магнитного по­ля в мейсснеровской фазе можно представить следующим образом: экранирующие токи, полностью компенсирующие внешнее магнитное поле внутри образца, сообщают образ­цу (цилиндрической формы) магнитный момент М или на­магниченность J = M/V, где V—объем образца. Намагничен­ность СП соответствует намагниченности идеального диамагне-тика с восприимчивостью =-1. Эта намагниченность пропор­циональна Н (в случае длинного цилиндра, ось которого па­раллельна полю Н).

Начиная с некоторого критического значения поля Н сверхпроводимость разрушается. Это связано с тем, что в достаточно сильном магнитном поле оба противоположно на­правленных спина электронов в куперовской паре будут стре­миться к одинаковой ориентации. Магнитное поле как бы разворачивает спин одного из электронов куперовской пары, и тем самым разрушает ее, что приводит к исчезновению сверхпроводимости при Н>Н_с. Поле Н_с называют парамаг­нитным критическим полем. Такой механизм разрушения куперовских пар называют «парамагнитным». Но есть и дру­гой механизм. Поскольку импульсы электронов в куперов­ской паре противоположны, то в магнитном поле на элект­ронные пары действуют противоположно направленные силы Лоренца, что приводит к движению электронов в противопо­ложные стороны и разрушению куперовских пар. Этот меха­низм разрушения называют орбитальным, Для «массивного» СП, т.е. СП с явно выраженным экранированием, это кри­тическое поле В_c идентично термодинамическому крити­ческому полю В_сt. Это сверхпроводники I рода. Рассмотрим термодинамику процесса разрушения СП магнитным полем. Термодинамический потенциал G (энергия Гиббса или сво­бодная энтальпия) для СП в магнитном поле имеет вид:

(5.2.23)

где Н — энтальпия; U — внутренняя энергия; S — энтропия; Р — давление; V —объем; М_m— магнитный момент сверхпро­водника (магнитный момент М_т всегда либо параллелен, ли­бо антипараллелен В).Поскольку приращение внутренней энергии

dU = TdS +A=TdS—PdV+BdM, то

dG = — SdT+VdP—MdB (dV<0) (5.2.24)

Р
ассматриваем СП при постоянном давлении, переменный параметр—температура. Пусть внешнее поле отсутствует. При температурах ниже T_c СП фаза является термодинами­чески устойчивой, т.е. для Т<Т_c функция Гиббса G_s, дол­жна быть меньше функции Гиббса нормального металла G_n. При Т = Т_c должно выполняться равенство G_s,= G_n. При на­ложении внешнего магнитного поля с ростом В функция G_s возрастает и при В>В_c. G_s, становится больше G_n т.е. СП фаза оказывается нестабильной. Функция Гиббса нормальной фазы практически не зависит от магнитного поля, так как индуцированные магнитные моменты атомов в нормальном металле малы.

Рис. 5.2.11. Фазовая диаграмма СП. Область устойчивости СП состоянии заштрихована

С

учетом соотношений

G_n(В)-G_n(0)=0 (5.2.25)

G_n(В_c)-G_s(B_c)=0

для длинного цилиндрического СП образца в продольном по­ле

M=JV_s=*B/₀*V_s= -B/₀*V_s получим

где V_s — объем образца; J — намагниченность. Определив экспериментально зависимость В_c(Т), можно количественно определить G_n-G_s (рис. 5.2.11). Удельную теп­лоемкость сверхпроводников можно выразить, используя формулы для разности термодинамических потенциалов G_n-G_s и связь теплоемкости при постоянном давлении с тер­модинамическим потенциалом

C_p=T(∂S/∂T)_P,B=-T(∂²G/∂T²)_P,B (5.2.27)

Получим для разности теплоемкостей в нормальном и сверхпроводящем состояниях

C_n-C_s=-VT/₀[(∂B_c/∂T)²+B_c ∂²B_c/∂T²] (5.2.28)

при V=const. При Т = Т_c С_s>С_n, так как при T_c критическое поле В_c=0. При Т_c теплоемкость испытывает скачок, равный

(C_c-C_s)_T=Tc= VT_c/₀(∂B_c/∂T)²_T=Tc (5.2.29)

Поскольку ∂²B_c/∂T²<0 и с понижением температуры ∂B/∂T уменьшается, то при некоторой температуре 0<Т<Т_с С_n=С_s,. При еще более низких температурах С_s<С_n. Для обычного проводника теплоемкость складывается из элект­ронной составляющей и решеточной теплоемкости. При пере­ходе в СП состояние вклад решетки в удельную теплоемкость практически не изменяется, т. е. скачок теплоемкости опре­деляется только электронной составляющей (это справедли­во, по крайней мере, для классических низкотемпературных СП). Теория БКШ для низких температур (T→0) даст сле­дующую зависимость:

С_s = 9,17 γ T ехр(-1,5 T_c/T) (5.2.30)

где γ =-(V/₀)В_c(∂²B_c/∂T²), (γ — константа Зоммерфельда для электронной системы).

Экспоненциальная температурная зависимость теплоем­кости от температуры, наблюдаемая экспериментально, яв­ляется еще одним прямым доказательством существования энергетической щели.

Р

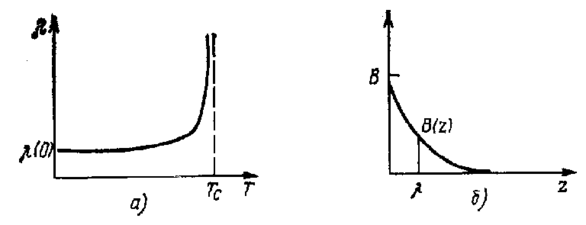
ассмотрим, каким образом осуществляется переход из СП I рода в нормальное состояние. Глубина проникновения магнитного поля резко возрастает при приближении к тем­пературе перехода T_c (температурная зависимость глубины проникновения λ изображена на рис. 5.2.12а, формула 5.2.8). Приповерхностный слой, в который проникает магнитное по­ле (рис. 5.2.12 6), оказывает тем большее влияние на свойства образца, чем меньше размеры образца. Поэтому для малых образцов можно ожидать меньшие значения |χ| по сравне­нию с массивными образцами (большее отклонение от иде­ального диамагнетизма).

Рис.5.2.2 Поведение магнитного поля в сверхпроводнике I рода

Для пленочных образцов с толщи­ной d<< λ магнитное поле практически равномерно пронизы­вает всю пленку. Однако величина критического поля при уменьшении толщины пленки возрастает. Это связано с тем, что вследствие уменьшения диамагнетизма пленки необходи­мо прикладывать все более сильные магнитные поля для то­го, чтобы выровнять значения свободных энтальпий G_n и G_s, (см. формулу 5.2.25). Для понимания поведения СП I рода в магнитном поле необходимо рассмотреть плотность экра­нирующих токов, которая связана с распределением магнит­ного поля уравнением Максвелла rotB=μ_oj_s. Плотность эк­ранирующих токов уменьшается по мере удаления от поверх­ности в глубь СП. Для поля, направленного по оси z,

(5.2.31)

где е_y — единичный вектор вдоль оси y.

Т

огда

(5.2.32)

где j₀ — плотность тока на поверхности; j₀=В₀/λμ₀.

Для тонких пленок

(

5.2.33)

С
оответствующее распределение плотности тока показано на рис.5.2.13. С уменьшением толщины пленки плотность эк­ранирующего тока на поверхности для заданного поля B₀ падает.

Рис. 5.2.13. Распределение плотности экранирующих токов j_s(x) по сече­нию тонкой сверхпроводящей пленки в магнитном поле, параллельном ее поверхности

Таким образом, в СП, у которых по крайней мере одно измерение сравнимо с глубиной проникновения, возрастает величина В_с. Можно было бы ожидать, что при достижении критического поля СП разобьется на очень тонкие чередующиеся участки нормальной и СП фаз толщиной меньше глу­бины проникновения, способных выдерживать сильные маг­нитные поля, оставаясь в устойчивом состоянии. Однако опыт показывает, что при достижении критического, поля СП со­стояние становится неустойчивым. Следовательно, расслоение на тонкие области энергетически невыгодно. Действительно, образование поверхности раздела между нормальной и СП областями связано с дополнительной энергией. Поверхност­ная энергия определяет магнитную структуру промежуточно­го состояния, когда СП I рода не является ни полностью СП, ни полностью нормальным. Рассмотрим такое состояние на примере СП шара в однородном внешнем поле. Выталкива­ние магнитного поля приводит к повышению напряженности поля у поверхности шара в области его экватора. Повыше­ние напряженности определяется коэффициентом размагни­чивания. Эффективное магнитное поле для шара вблизи эк­ватора В_эфф= (3/2)B_е (N = l/3). Если В_эфф=В_с, то СП вблизи экватора должна разрушаться. Однако весь шар не может перейти в нормальное состояние, так как в этом случае поле проникло бы внутрь шара и стало бы равно внешнему полю, т.е. оказалось бы меньше критического. Сверхпроводник пе­реходит в промежуточное состояние, т.е. расслаивается на нормальные и сверхпроводящие области, причем границы должны ориентироваться параллельно магнитному полю. Поскольку образование межфазных границ требует затраты энергии, то слои не могут быть сколь угодно тонкими. Heo6ходимая энергия для образования границ между фазами за­бирается у магнитного поля.

Не так обстоит дело в случае сверхпроводников II рода. Возможны условия, при которых образование границы разде­ла не только не требует дополнительной энергии, но и свя­зано с выигрышем энергии.

Характеристики

Список файлов учебной работы