[5] Сверхпроводники (987503), страница 5

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 5)

Сверхпроводники, для которых выполняются эти условия, называются СП II рода. Можно показать, что выигрыш энер­гии при образовании границы раздела получаем, если λ=ζ, где λ — глубина проникновения поля, ζ — длина когерентно­сти. При этом

ζ,B_ct²< λB², т.е. B_ct²/B² <λ/ζ,

где B_ct, — термодинамическое поле, соответствующее условию 5.2.26.

Поэтому следует ожидать, что в сверхпроводниках, у ко­торых. λ>ζ, магнитное поле может проникать уже при полях В, меньших B_ct. Оказывается, что в этом случае поверхностная энергия границы раздела «нормальная фаза — СП» от­рицательна, и энергетически выгодно не скачкообразное про­никновение поля сразу в весь объем образца, а образование смешанного состояния. При этом, как и на границах раздела, возникают неоднородности в пространственном распределении поля В и плотности куперовских пар n_s. Условие λ>ζ можно получить, если мала l* (длина свободного пробега). При уменьшении l* глубина проникновения λ слабо возрастает, а длина когерентности падает, как l*, т.е. это СП с доста­точным количеством примесей.

Р
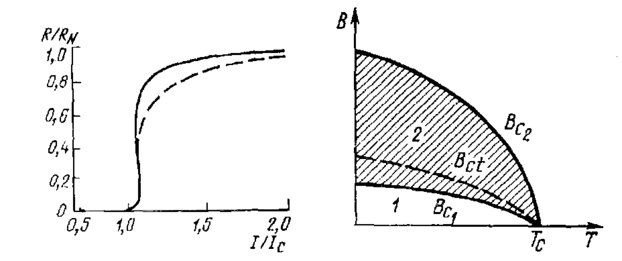
азличие между СП I и II рода особенно заметно прояв­ляется в форме кривой намагниченности (рис. 5.2.14).

Рис. 5.2.14. Кривая намагничивания СП II рода

Картина разрушения сверхпроводимости магнитным полем в сверхпроводниках II рода подробно рассмотрена Абрико­совым. В смешанном состоянии СП как бы пронизан нитями (рис. 5.2.15). Нить представляет собой тонкую область нор­мальной фазы, ориентированной вдоль вектора В. Причем каждой нити соответствует ровно один квант магнитного потока.

Р
ис.5.2.15 Абрикосовские вихри в СП II рода в магнитном поле

Формирование областей в форме нитей — абрикосовских вихрей начинается сразу, как только магнитное поле превысит значениеB_с1 число абрикосовских вихрей увеличи­вается с ростом поля до В = В_с2. В смешанном состоянии при Bc₁<B<B_С2 магнитное поле частично проникает в сверхпро­водник, при этом уменьшается от 1 до 10^-5 при В> B_С2. Такое смешанное состояние называют также фазой Шубникова. В смешанном состоянии в пространстве между вихря­ми сверхпроводимость сохраняется и сопротивление образц равно нулю. Конечное сопротивление появляется при ВВ_С. Рассмотрим подробнее характер перехода сверхпроводника из СП фа­зы в нормальную для сверхпроводни­ков I и II рода. Каким же образом осуществляется этот переход? Как отмечалось в предыдущем разделе, раз­рушение куперовских пар происходит при значениях плотности тока, превы­шающих некоторое критическое зна­чение. При малых плотностях тока сверхпроводник находится в мейсснеровской фазе, т.е. маг­нитное поле не проникает в глубь СП.

Рис. 5.2.16 Распределение плотности тока (а) и магнитного поля (б) в СП с транспортным током (В_рез=2В_е+₀I/2R

В_эфф=2 В_е т.к. N=1/2) I— ток, R—ра­диус проволоки

Рис.5.2.17. Зависимость критического тока проволоки круглого сечения от внешнего магнитного поля В_е, перпендикулярного оси проволоки

Но это означает, что внутри сверхпроводника не может протекать ток, так как он создавал бы там магнитное поле. На рис. 5.2.16 а показано распределение плотности тока, протекающего через сверхпро­водник (так называемого транспортного, в отличие от кру­говых экранирующих токов), по сечению цилиндрического проводника. На рис. 5.2.16 б изображено магнитное поле, со­здаваемое этим током. В «пассивных» (сплошных) сверхпро­водниках с полностью сформированным экранирующим слоем критическая плотность тока будет соответствовать критическому значению индукции В_с, и критический ток будет иметь такую же температурную зависимость, как и критическое магнитное поле. Плотность j_c связана с глубиной проникно­вения магнитного поля следующим приближенным соотноше­нием (считаем, что плотность тока постоянна на глубине проникновения поля, а затем уменьшается скачком до нуля):

j_с = I_c/(2R )5*10⁷ А/см²

(R = 0,5 см; = 5,110^-6 см; j_с = 7,5 А).

Критические плотности тока велики, и если бы не эффект экранирования, который приводит к выталкиванию тока в топкий приповерхностный слой, то через СП можно было бы пропускать очень большие токи.

Для вычисления критического тока СП, помещенного во внешнее магнитное поле, необходимо сложить (векторно) внешнее магнитное поле с полем транспортного тока на по­верхности.

Рис.5.2.18. Зависимость сопротивления. СП от величины транспортного тока

Рис.5.2.19. Фазовая диаграмма СП II рода:1—мейсснеровскаи фаза;

2 — шубниковская фаза

На рис. 5.2.17 приведена зависимость критического тока от внешнего магнитного поля В_е, при постоянной температуре, т. е. постоянном В_с.

Каким образом происходит переход сверхпроводника в нор­мальное состояние при достижении критической силы тока?

Предположим, что по всему объему переход происходит одновременно. Но тогда ток перераспределится по всему сечению СП и его плотность окажется меньше критической, т.е. должно снова возникнуть сверхпроводящее состоя­ние. Таким образом, образец не сразу весь переходит в нор­мальное состояние, а вначале переходит в промежуточное состояние, т. е. в нем появляются участки с нормальной про­водимостью. При токе J_c появляется скачком сопротивление, • которое насыщается при дальнейшем увеличении тока (рис. 5.2.18).

Аналогичный переход в промежуточное состояние проис­ходит и во внешнем магнитном поле (см. предыдущий па­раграф).

Рассмотрим теперь сверхпроводники II рода. В слабых магнитных полях и при малых транспортных токах СП II ро­да также находятся в мейсснеровской фазе, т.е. выталки­вают магнитное поле и ток в тонкий приповерхностный слой. Если магнитное поле превышает B_С1 (рис. 5.2.19), то СП II ро­да переходит в шубниковскую фазу, в СП проникают нити магнитного потока. В этой фазе СП II рода даже при очень слабых транспортных токах обладает конечным сопротивле­нием. Происходит проникновение магнитного потока и тока в глубь СП, причем транспортный ток течет и сквозь нити потока, т.е. через области, в которых существует магнитное поле. Между током и потоком возникает сила взаимодейст­вия, под действием которой нити потока должны перемещать­ся перпендикулярно направлению тока и магнитного поля, т. е. перпендикулярно своей собственной оси.

Движение вихревых нитей по СП приводит к появлению потерь, т.е. электрическая энергия превращается в тепло. На образце при этом появляется разность потенциалов, обуслов­ленная конечным сопротивлением образца.

Превращение электрической энергии в тепловую при дви­жении вихревых нитей происходит за счет двух процессов. Первый связан с появлением локальных электрических полей при изменении магнитного поля при прохождении нитей. Эти поля ускоряют неспаренные электроны, которые отдают свою энергию решетке. Второй процесс связан с неоднородностью и изменением плотности куперовских пар n_s в вихре. Плотность n_s, изменяется от нуля в центре вихря до определенного конечного значения на некотором удалении от него. Для уста­новления равновесного значения n_s, после отклонения от это­го равновесия необходимо конечное время релаксации. Если вихри движутся медленно, то энергия, затрачиваемая на раз­рыв куперовских пар на переднем фронте движения вихря, снова освобождается позади него при образовании пар. При быстром движении вихря равновесная плотность куперовских пар не успевает устанавливаться и вследствие временных изменений n_s, происходит рассеяние энергии (так как на пе­реднем фронте вихря разрыв куперовских пар требует мень­ше тепла, чем его выделяется при повторном спаривании электронов вследствие того, что магнитное поле на переднем фронте превышает равновесное значение).

П
оскольку в идеальных сверхпроводниках II рода сколь угодно малые транспортные токи ведут к смещению вихрей, то критический ток идеального сверхпроводника в состоянии шубннковской фазы равен нулю.

Рис. 5.2.20. Зависимость намагни­ченности от индукции внешнего магнитного поля для СП II рода и III рода

Конечные критические токи в шубниковской фазе можно получить только в том случае, если вихревые нити будут ка­ким-либо образом связаны с теми участками вещества, че­рез которые они проходят. Это закрепление (пиннинг) вих­ревых нитей можно осуществить. Сверхпроводники II рода, содержащие центры закрепления вихрей (центры пиннинга), называют сверхпроводниками III рода. Они уже могут найти техническое применение.

В сверхпроводниках III рода вихревые нити шубников­ской фазы прочно связаны с определенными энергетическими предпочтительными участками вещества. Следствием этого является то, что во внешнем поле не может установиться намагниченность, соответствующая термодинамическому рав­новесию.

Для таких веществ кривая намагниченности имеет иной вид (рис. 5.2.20).

Эти СП имеют большое значение намагниченности. Это означает, что образец с дефектами может обладать почти идеальным диамагнитным экранированием в полях, превосхо­дящих B_С1. Кроме того, отсутствует обратимость. При снятии внешнего поля магнитный поток остается как бы «заморо­женным» в образце. Не изменяется только верхнее критиче­ское поле В_С2,, которое определяется длиной свободного про­бега l*, достаточно малой в этих сверхпроводниках (допол­нительные нарушения уже не влияют заметно на l*). Увели­чение В_С1 можно объяснить следующим образом: проникнове­ние вихревых нитей в приповерхностный слой образца увели­чивает эффективную толщину экранирующего слоя и тем са­мым экранирующий ток.

При поле В_С2 плотность куперовских пар равна нулю и сверхпроводимости нет. Магнитное поле равномерно прони­зывает весь образец. Если теперь понижать внешнее поле, то образец снова перейдет в шубниковскую фазу. Магнитный поток разобьется на кванты магнитного потока Ф₀, а вихре­вые нити .будут закреплены на дефектах решетки. При по­нижении внешнего поля они с трудом будут покидать мате­риал и даже при В_е= 0 останется некоторый замороженный магнитный поток, направленный вдоль внешнего поля (т.е. парамагнитный поток).

Наиболее эффективными центрами пиннинга являются включения нормальных фаз в СП. Чтобы «сорвать» вихри с центров их закрепления, необходимо сообщить некоторую по­роговую энергию. Поэтому в таких СП возможно протекание тока без сопротивления, т.е. СП тока. Если же транспортный ток превышает критическое значение, при котором сила Ам­пера, действующая на нити, будет превышать силу пиннинга, начинается движение вихревых нитей, т.е. появится сопро­тивление.

Таким образом, в СП III рода необходимо повысить силу пиннинга, чтобы достичь максимальных значений критиче­ских токов.

При движении вихревых нитей значительные потери энер­гии обусловлены появлением локальных электрических полей, воздействующих на неспаренные электроны, т.е. сопротивле­ние в таком состоянии будет зависеть от нормального сопро­тивления материала R_N.

5.2.6. Модели высокотемпературной сверхпроводимости

Как видно из п.5.2.3, основное условие для возникновения сверхпроводимости — наличие притяжения между электрона­ми вблизи поверхности Ферми, приводящего к образованию пар с равными нулю полным спином и импульсом (бозе-частицы). Такое взаимодействие возникает как результат того, что два электрона обмениваются элементарными возбужде­ниями систем, ответственной за взаимодействие. Эти эле­ментарные возбуждения должны распространяться с очень слабым затуханием, чтобы существовало необходимое дальнодействующее взаимодействие.

В классических сверхпроводниках в качестве системы, от­ветственной за возбуждение, выступает кристаллическая ре­шетка, а элементарным возбуждением является фонон (фононный механизм сверхпроводимости). Но роль такого эле­ментарного возбуждения могут играть и другие возбуждения в кристаллах, такие как магноны (кванты спиновых волн в спиновой системе атомов решетки), плазмоны (коллективные возбуждения электронов в металлах и полупроводниках с высокой концентрацией носителей), в качестве таких возбуж­дений могут выступать и экситоны. В соответствии с типом элементарных возбуждений были предложены механизмы сверхпроводимости — спиновый (Маттиас, Копаев, Савченко, Стефанович), экситонный (Литтл, Гинзбург), плазменный, последний маловероятен (плазменная частота слишком ве­лика).

Согласно теории БКШ критическая температура начала перехода в сверхпроводящее состояние определяется выра­жением

Характеристики

Список файлов учебной работы