Теория подобия и анализ размерностей (2012) (849561), страница 14

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 14)

С целью определения и возможности дальнейшей оценки концентрационных границ области устойчивого горения вихревых горелок, в полученную систему определяющих критериев введем величину коэффициента избытка воздуха

. (7.13)

Допустим, что одной из основных целей работы является исследование низкоперепадного вихревого горелочного устройства, поэтому в искомую систему критериальных зависимостей и основанную на ней методику расчета включим безразмерный комплекс, характеризующий степень расширения потока в камере сгорания вихревой горелки:

. (7.14)

Дополнительные критерии, необходимые для моделирования горелочных устройств противоточного типа, составим на основе безразмерных комплексов, характеризующих геометрическое подобие проточной части вихревых горелок. На основе исследований и обобщения расчетных и экспериментальных данных можно сделать заключения, что целесообразно среди различных комбинаций выбрать два характерных параметра и .

Первый представляет собой относительную площадь соплового ввода закручивающего устройства:

. (7.15)

Вторым характерным геометрическим параметром является относительный радиус отверстия сопла диафрагмы, из которого происходит истечение продуктов сгорания:

. (7.16)

Используя характерные масштабы величин, входящих в состав записанных безразмерных комплексов (рис. 7.1), запишем критерии, определяющие рабочий процесс вихревой противоточной горелки:

Рис. 7.1 Расчетная схема к выбору масштабов физических величин в противоточной вихревой горелке

(7.17)

Таким образом, записанная система критериев термогазодинамического, химического и геометрического подобия достаточна для приближенного моделирования вихревых горелочных устройств противоточного типа, в том числе и низкоперепадных, а их интегральные характеристики, определение и оценка которых важна на стадии проектирования новых конструкций горелок, являются однозначными функциями записанных безразмерных критериев. Вид функциональной зависимости можно получить в результате обработки эмпирических данных. Искомые характеристики будем записывать в виде зависимостей от определяющих критериев, и безразмерных переменных, составленных из размерных физических величин, значение одной из которых известно, а другой определяется эмпирически. Такими параметрами, например, являются: степень повышения температуры (безразмерная среднемассовая температура факела продуктов сгорания) , относительная длина зоны горения , коэффициент расхода горелки , безразмерная тепловая мощность .

Обобщая приведенные рассуждения, составим критериальную модель расчета параметров рабочего процесса низкоперепадных вихревых горелочных устройств противоточного типа. В общем виде функциональная связь между полученными критериями имеет вид

. (7.18)

Зависимость интегральных характеристик вихревых горелок от влияющих на них факторов будем определять в виде

; (7.19)

– срывные характеристики в области бедных и богатых топливовоздушных смесей

; (7.20)

– степень повышения температуры

; (7.21)

– гидравлические и расходные характеристики

; (7.22)

;

– эмиссионные характеристики

; (7.23)

– оценка механизма горения

. (7.24)

В итоге искомая система критериальных уравнений примет вид

(7.25)

Вид аппроксимирующих функций критериальной модели параметров рабочего процесса противоточных вихревых горелок определяется обработкой данных, полученных эмпирически с использованием теории планирования эксперимента. Часто, когда вид аппроксимирующих уравнений функций отклика заранее неизвестен, их представляют в виде полиномов третьей степени. В общем случае система уравнений (7.25), связывающих критерии подобия, имеет вид:

,

где – функции отклика; – факторы.

К факторам предъявляются следующие требования: управляемость факторов при проведении экспериментов; непосредственное влияние факторов на характеристики устройства; однозначность и некореллируемость факторов; возможность представить факторы в безразмерном виде для обезразмеривания коэффициентов, входящих в уравнение регрессии; независимость факторов, т. е. возможность одновременно изменять значения всех факторов.

Рассмотрим пример получения коэффициентов эмпирического уравнения для определения характеристик срыва пламени методом наименьших квадратов. Функции коэффициента избытка воздуха и , решения которых соответствуют границам устойчивой работы (срывным характеристикам), будем аппроксимировать уравнениями:

(7.26)

(7.27)

Коэффициенты и , входящие в уравнения, определяются методом наименьших квадратов, при условии минимума функций невязки . Это условие записывается следующим образом

. (7.28)

Функция невязки показывает разность между экспериментальными и вычисленными по уравнению регрессии значениями функции отклика в -й экспериментальной точке.

При поиске аппроксимирующих уравнений для всех функций отклика составляется переопределенная система уравнений, кроме того, не исключена возможность появления противоречивой системы. Это приводит к тому, что система может иметь бесконечно много решений или не иметь решений. Переопределенность возникает, когда число уравнений больше числа неизвестных, противоречивость – когда некоторые из уравнений несовместимы друг с другом. Только если все экспериментальные точки лежат на одной линии (или n-мерной поверхности, в зависимости от числа факторов), то система становится определенной и имеет единственное решение. Метод наименьших квадратов с условием (7.28) обладает свойством преобразовывать в определенную любую произвольную систему уравнений.

Для определения двадцати неизвестных коэффициентов или требуется система из двадцати уравнений. Она получается следующим образом. Условие (7.28) записывается в виде

(7.29)

и

(7.30)

.

Минимум этих функций, если он существует, достигается при одновременном равенстве нулю частных производных по всем неизвестным коэффициентам, т. е.

(7.31)

и .

Значения функций отклика и находятся по результатам полного трехфакторного эксперимента, матрица которого имеет вид

(7.32)

.

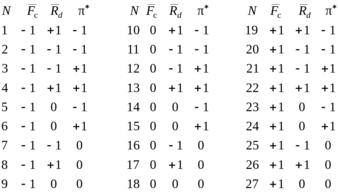Матрица (7.32) строится следующим образом. Факторами являются , и , – номер опыта. Знак минус означает, что в данном опыте тот или иной фактор имеет минимальное значение, ноль – среднее, плюс – максимальное в выбранной области определения. Поскольку число факторов равно трем и каждый базируется на трех уровнях, то количество опытов, необходимое для реализации всех возможных сочетаний уровней факторов, определяется следующим образом: , где – количество факторов. Качество построения матрицы планирования эксперимента во многом определяет качество эмпирических уравнений. Оценки коэффициентов должны быть наилучшими, и точность предсказания функции отклика не должна зависеть от направления в факторном пространстве, поскольку заранее не известно, где следует искать ее оптимальные значения. Поэтому при построении матрицы (7.32) обязательным является выполнение следующих условий.

1. Симметричность матрицы относительно центра эксперимента. Математическая формулировка этого условия выглядит следующим образом: алгебраическая сумма элементов столбца каждого фактора равна нулю:

, (7.33)

где – число опытов; – номер фактора, .

2. Условие нормировки: сумма квадратов элементов каждого столбца равна числу опытов

. (7.34)

3. Условие ортогональности матрицы планирования: сумма почленных произведений любых двух столбцов матрицы равна нулю

, , . (7.35)

Решения регрессионного уравнения образуют поверхность в четырехмерном пространстве, точки которой соответствуют значениям коэффициента избытка воздуха и , при которых происходит нарушение устойчивой работы вихревого горелочного устройства (срыв пламени). Решения этих уравнений находятся при любых значениях факторов , принадлежащих области их определения. Подобная процедура получения коэффициентов может быть выполнена для любого вида критериальных уравнений: полиномиального, степенного, экспоненциального и т. д. Для примера критериальные уравнения границы бедного срыва пламени имеют вид:

– полиномиальная зависимость

Характеристики

Список файлов книги