r1 (1123690), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

Так как поведение помехи N считается известным и неизменным (_N()), то описание суммарного сигнала возможно в предположении, что исходный сигнал принимает некоторое фиксированное значение из пространства S. В этом случае может быть найдена условная плот­ность распределения суммарного сигнала (X) = (X₁, X₂, X₃, …, X_n/S).

Задача решающего устройства состоит в том, чтобы по анализу суммарного сигнала оптимальным образом решить какой именно сигнал присутствует на входе или какие значения имеют параметры исходно­го сигнала. Оптимальность решения состоит в том, чтобы сделать как можно меньше ошибок в принятии решения или как можно точнее определить параметры входного сигнала.

Все возможные решения, которые может сделать решающее уст­ройство, называются пространством решений Г. Каждое возможное ре­шение из пространства решений будем обозначать . Пространство решений должно быть известно заранее.

Полное описание процесса решения может быть сделано заданием плотности вероятности того, что при условии появления фиксированного сигнала Х на входе решающего устройства будет получено решение . То есть каждому значению случайной величины Х соответствует плотность распределения .

Эта условная плотность вероятности обозначается (/Х) и на­зывается решающей функцией. Решающая функция может быть детерминирована (не случайна) или рандомизирована.

При детерминированной решающей функции каждому значению слу­чайной величины X соответствует одно единственное решение . Т.е между решением  и сигналом X существует регулярная зависимость

 = (Х)

При рандомизированной решающей функции каждому значению слу­чайной величины X может соответствовать несколько решений в соот­ветствии с некоторым распределением вероятностей этих решений. В дальнейшем мы будем пользоваться только детерминированными решающими функциями. Пример детерминированной решающей функции

X 

₁

Решающее устройство

(/X)

₀

Функция ошибок.

Поскольку реальный сигнал S и помеха N являются случайными величинами, то принимаемый сигнал Х = S + N также является случай­ной величиной. Так как X - случайная величина, то принимаемые по его значениям решения  относительно сигнала S могут быть как правильными, так и ошибочными.

Ведем понятие платы за принятое решение.

За каждое решение (правильное или не правильное) вносится оп­ределенная плата. В качестве меры платы выбирают платежную функцию. Мера платы зависит от сигнала S (S > 0 или S = 0 для нашего примера, смотри выше) и от принятого решения . Принято, что за правильное решение вносится нулевая плата. Поэтому платежную функцию часто называют функцией потерь за ошибочные решения и обозначают как F(S, ). Ввиду случайного характера S и , функция F(S, ) так же носит случайный характер. Поэтому для оценки ка­чества решения принимается не сама функция, а ее математическое ожидание, называемое средним риском.

Так как между решением  и сигналом X существует регулярная зависимость  = (X), т. е. каждому значению случайной величины X соответствует одно единственное решение , то последнее выражение можно переписать в виде:

Для дискретной функции потерь выражение для математического ожи­дания имеет вид:

или

при этом функция потерь приобретает вид матрицы:

P(S) - априорная вероятность появления полезного сигнала S

Р(/S)- вероятность принятия решения  при условии, что в принятом сигнале X присутствует полезный сигнал S

Учебный вопрос 3.

Применение теории статистических решений к задачам обнаруже­ния радиолокационных сигналов.

1. постановка задачи.

Пусть производится некоторый статистический эксперимент (при­ем и анализ радиолокационных сигналов). Объектом эксперимента яв­ляется случайная величина X. Случайная величина X представ­ляет собой смесь сигнала S и помехи N.

X = S + N

Относительно помехи известно, что помеха присутствует всегда N > 0

Относительно сигнала известно, что S может принимать два зна­чения

1. S = S₀, где S₀ = 0

S = S₁, где S₁ > 0

Относительно СВ X известно, что она принадлежит к одному из двух распределений

₀(Х), или ₁(Х).

₀(Х) - соответствует распределению сигнала X вида Х = S₀ + N, т. е. распределению помехи.

₁(Х) - соответствует распределению сигнала X вида X = S₁ + N, т. е. распределению сигнала и помехи.

По которому из двух законов она распределена мы не знаем и можем только строить гипотезы. Существуют две гипотезы:

1. гипотеза Н₀ - СВ X распределена по закону ₀(Х);

2. г

   
   
   
   
   

   ₀(Х)

   
   

   ₁(Х)

   
   ипотеза Н₁ - СВ X распределена по закону ₁(Х).

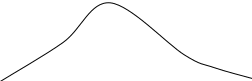
Плотности распределения случайной величины X

Цель эксперимента состоит в проверке, что СВ X распределена по закону ₀(Х).

Все возможные результаты эксперимента со случайной величиной X = {x₁, x₂, x₃, …, x_n} можно изобразить на оси x (рис )

На основании результатов эксперимента необходимо принять ре­шение () о том, правильна или ложна гипотеза Н₀.

Для того, чтобы принимать решение необходимо предварительно установить некоторый критерий или правило решения.

Установить правило решения - это значит каждому х_i из области и поставить в

соответствие либо гипотезу Н₀, либо гипотезу Н₁, т.е. разбить область X на две части: ₀ и ₁, для одной из которых бу­дем считать верной гипотезу Н₀, а для другой верной гипотезу Н₁.

Область ₀ - область принятия гипотезы Н₀ - (решение ₀);

x

x x₂ …… x _i ……. x _n-1 x _n

область принятия гипотезы H₀ область принятия гипотезы H₁

Область ₁ - область принятия гипотезы Н₁ - (решение ₁);

Каким же образом устанавливать решающее правило?

1. отношение правдоподобия

Введем очень важное в теории принятия решений понятие отноше­ния правдоподобия.

Поскольку мы говорим о гипотезах, то представим наши плотности распределения в виде условных плотностей: Пусть

₀(X) = (X/H₀) - плотность вероятности результатов эксперимента при условии, что верна гипотеза Н₀.

₁(X) = (X/H₁) - плотность вероятности результатов эксперимента при условии, что верна гипотеза Н₁.

Предположим, что известна плотность вероятности n-мерной вы­борки исследуемой СВ при условии что, гипотеза Н₀ верна. Эту ус­ловную плотность вероятности можно представить в виде (x₁, x₂, x₃, …, x_n/H₀). Аналогично будем считать заданной условную плотность вероятности n-мерной выборки соответствующей гипотезе Н₁: (x₁, x₂, x₃, …, x_n/H₁).

Составим отношение

,

Это выражение является непрерывной функцией выборки (x₁, x₂, x₃, …, x_n) и называется отношением правдоподобия. Для нахождения числового значения отношения правдоподобия должен быть задан явный вид функций плотностей вероятностей. Задача обнаружения сигнала в ра­диолокации сводится к построению и анализу отношения правдоподо­бия.

Пусть функции плотностей вероятностей заданы в явном виде (x₁, x₂, x₃, …, x_n/H₀), (x₁, x₂, x₃, …, x_n/H₁). Пусть известны результа­ты эксперимента (x₁, x₂, x₃, …, x_n). Решение о наличии или отсутствии сигнала проводится по следующей схеме:

Если значение функции плотности (x₁, x₂, x₃, …, x_n/H₁) не менее чем в l₀ раз превосходит значение функции плотности (x₁, x₂, x₃, …, x_n/H₀),

(x₁, x₂, x₃, …, x_n/H₁) > l₀(x₁, x₂, x₃, …, x_n/H₀)

или в виде отношения правдоподобия

то принимаем решение о справедливости гипотезы Н₁ (решение ₁), в противном случае принимается решение о справедливости гипотезы Н₀ (решение ₀).

Решающее правило записывается следующим образом:

Примечание !!! Мы пока не поднимаем вопроса - из каких сооб­ражений выбираем значение l₀

Поскольку решение должно быть однозначным, возможны ошибки ре­шения. Ошибки могут быть двух родов.

1. Ошибка первого рода состоит в том, что гипотеза Н₀ отвер­гается, когда она верна на самом деле (т.е. принимается решение Н = Н₁, когда на самом деле Н = Н₀ - ЛОЖНОЕ ОБНАРУЖЕНИЕ). Ошибке перво­го рода ставится в соответствие ее вероятность - Р_ло.

P_ло = Р(Х ₁/Н₀)

1. Ошибка второго рода состоит в том, что гипотеза Н₀ не от­вергается, когда она на самом деле является ложной (т.е. принима­ется решение Н = Н₀, когда на самом деле Н = Н₁ - ПРОПУСК ЦЕЛИ). Ошибке второго рода ставится в соответствие ее вероятность - Р_пр.

P_пр = Р(Х ₀/Н₁)

Тогда условные вероятности ошибок первого и второго рода оп­ределяется выражениями:

ПРИМЕР

Пусть наблюдаемые значение случайной величины X расположены в диапазоне всех действительных чисел.

Пусть Н₀ - гипотеза о том, что случайная величина X подчинена нормальному закону с нулевым математическим ожиданием (m_х = 0) и единичной дисперсией (_х = 1).

Пусть Н₁ - гипотеза о том, что случайная величина X подчинена нормальному закону с математическим ожиданием m_х = 1 и дисперсией _х = 1.

Характеристики

Список файлов учебной работы