Процессы с независимыми приращениями

§7 Процессы с независимыми приращениями.

7.1. Пусть E - линейное пространство, а  -s-алгебра борелевских множеств на нем. Через, где, обозначим "параллельный" сдвиг множества B на вектор x, точнее: .

Пусть  семейство вероятностных мер на  удовлетворяющих условиям:

i)    - -измеримая функция по x для ;

ii)    если   , то справедливо равенство

                                                              (38)

Очевидно следующее равенство

                                                     (39)

Рекомендуемые материалы

Действительно. Если , то равенство (39) очевидно. Стало быть, (39) справедливо для простых функций, поэтому, в силу теоремы о монотонной сходимости, равенство (39) остается справедливым для любой измеримой ограниченной функции.

Из (38) следует равенство

                                                    (40)

Из (39) следует, что если положить , то - будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для  Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то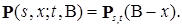 

7.2. Пусть q- вероятностная мера на и , где - вероятностная мера на , определенная формулой

 (41)

причем  где - переходная вероятность.

Определение. МПШ  со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для N, t_k Î R⁺,  t₁<t₂<…<t_n , случайные вектора  являются независимыми в совокупности, причем вектор - называется начальным значением процесса с распределением  q, называемым начальным распределением.

Таким образом, чтобы задать процесс с независимыми приращениями достаточно знать:

     а) начальное распределение вероятностей q случайного вектора,

     б) распределение вероятностей случайных векторов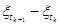

.

Очевидно, что если заданы q и , то соотношение (41) определено совместное распределение векторов .

Покажем теперь, что введенное таким образом совместное распределение определяет процесс с независимыми приращениями. Действительно, пусть ,где , и  ,тогда имеем:

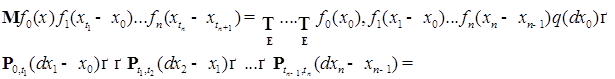
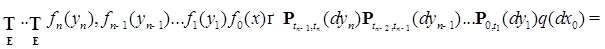
                                                (42)

Отсюда следует независимость векторов. Стало быть, для процесса с независимыми приращениями справедливо равенство где любая    для .

7.3. Процессы с независимыми приращениями (СПСП) удобно изучать с помощью характеристических функций. Пусть и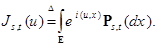

Тогда из (42) следует, что

.                        (43)

Очевидно, (43) эквивалентно условию, что процесс   является процессом с независимыми приращениями. Отсюда следует, что если и  удовлетворяют (43), то справедливо равенство

                                                           (44)

где . Очевидно, что (44) эквивалентно тому, что   - СПСП.

7.4. Определение. СПСП называется однородным (ОСПСП), если для любых  - случайный вектор имеет распределение, не зависящее от t, т.е..

Определение. ОСПСП называется стохастически непрерывным, если он непрерывен по вероятности.

Приведем теперь некоторые свойства ОСПСП. Пусть , тогда справедливы следующие утверждения:

1)  

Это равенство вытекает из (43). Отсюда, в частности, следует, что .

2)  Пусть  - ОСПСП. Если  ,то для , такого что . Доказательство этого утверждения приведите самостоятельно.

3)  . Действительно, пусть для любого существует  такое, что  для любых. Пусть. Из определения ОСПСП имеем

.

Так как для любого  u, такого что,   , то существует такое  (зависящее от N), что для любых  t < t_N  . Стало быть, существует функция  , т.е.  . Отсюда в силу свойства 1) получаем что  , для  ,  и . Поэтому существует функция такая, что . Значит 

,                                                                                     (44)

 где   можно определить следующим образом  

=,

причем сходимость равномерная по. Отсюда вытекает следующее свойство.

4) Для любых  существует функция , называемая кумулянтой, такая что  для любого.

7.5. Теорема 10 (Леви-Хинчина). Пусть ОСПСП со значениями в стахостически непрерывный. Тогда существуют:

i)  конечная мера П на  ii) a - n – мерный вектор;  iii) b - размера  положительно определенная матрица,

такие что для любого  такого, что  кумулянта  имеет вид:                       (46)

Замечание.  В  доказательстве теоремы 10  вместо формулы (46) удобнее воспользоваться следующей

(47)

где  ,    

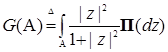
Доказательство. Пусть – распределение вероятностей процесса , а  соответствующая ему характеристическая функция. Положим для  B()  . Предположим, что семейство мер - слабо компактно. Пусть  - последовательность такая, что: a)  при ; б)   слабо сходится к некоторой мере  на B(). Тогда имеем

      (48)

где    

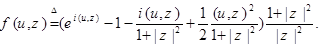
Так как , то - непрерывна и ограничена. Поэтому, в силу слабой сходимости  к  при , имеем

                                 .

Значит, при  и  существуют пределы       где - линейная функция, т.е. , а - положительно определенная квадратическая форма, т.е. , соответственно. Поэтому в (48) можно произвести предельный переход при , получим

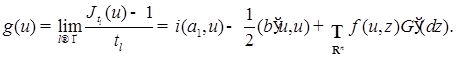
Пусть , где {0}- одноточечное множество, “состоящее” из точки “нуль”. Так как , то . Кроме того, интеграл существует и представляет собой положительно определенную квадратическую форму по u, т.е.  . Из приведенных построений следует, что . Поэтому существует положительно определенная матрица , такая что ,

 что и доказывает (47).

Установим слабую компактность семейства мер . В силу теоремы 36 главы 1 нужно установить, что: а) ; б) где .

Пусть , . В силу условий теоремы и (46), получаем, что для любого  существует такое  , что

, при                                (49)

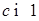
и при

, при .                              (50)

Так как    для  , то из (49) следует, что

                                   (51)

Нам понадобятся значения интегралов:

   

где  Г(k) - Гамма-функция,   - функция Бесселя, порядка m  действительного аргумента.  Проинтегрируем неравенства (49), (50) по , а затем получившийся результат разделим на  ,   (), имеем:

                (52)

        (53)

Рассмотрим (52), пусть  и , имеем

                                 .

Рассмотрим (53). Так как - ограничена, то можно выбрать (при любом   c>0)   таким, что 

                                                      (54)

Тогда имеем   .

Основы эмбриологии 2 - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Из вышеприведенных рассуждений следует, что , для любого t .

Заметим, что . Выберем теперь  таким, что левая часть (52) не превосходила , а cтаким, чтобы выполнялось (54). Тогда получаем, что  для любого t. Доказательство закончено.

7.6. Рассмотрим частные случаи формулы (47), когда n =1.

1)  Пусть  и для любого . В этом случае . Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке . Следовательно, , т.е. точка   движется с постоянной скоростью а.

2) Пусть  для любого. В этом случае приращения   имеют нормальное распределение со средним  и дисперсией равной . Если , то процесс  является гауссовским. Отметим, что если и , то такой процесс называется винеровским.

3) Пусть  и , а мера П сосредоточена в точке {1} и имеет в ней массу, равную единице. Тогда характеристическая функция будет иметь вид . Отсюда следует, что . Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3.