Диффузионные процессы

§8 Диффузионные процессы.

8.1. Определение. МПШ  называется диффузионным, если выполняются условия:

i) для  любого  и vравномерно по   , где - сфера радиуса ε  с центром в точке x, а ;

ii) существуют вектор-функция  и оператор

 такие, что для любых и  равномерно по

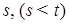
                                 (56),

                     (57),

при этом  n–мерная вектор-функция называется вектором сноса, а b(s,x)  матрица-функция размера  называется матрицей диффузии.

Рекомендуемые материалы

Будем обозначать через  i-ую компоненту вектора сноса, а через    - элемент матрицы диффузии.

8.2. Условия i), ii) неудобны для проверки, поэтому в данном пункте мы приведем достаточные условия того, что процесс  диффузионный.

Теорема 11. Для того чтобы  n-мерный МПШ  был диффузионным достаточно, чтобы соответствующая ему переходная вероятность  удовлетворяла условиям:

i) для некоторого , любого x равномерно по t

 ,

ii) существуют функции  и  такие, что для всех t, x 

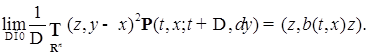
Доказательство. Проведем его для случая n=1. Действительно, в этом случае

,

,

.

Отсюда следует утверждение теоремы.

8.3. Теорема 12. Пусть  n-мерный диффузионный МПШ, а коэффициенты сноса и диффузии, соответственно, ,   -непрерывные по совокупности переменных функции. Пусть   непрерывная ограниченная функция такая, что  имеет непрерывные по совокупности переменных производные ,  для любых  . Тогда существует производная  и  удовлетворяет уравнению:

                   (58)

Доказательство. Пусть . Очевидно, что  ограниченная функция, поэтому в силу условия i)

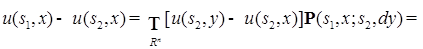
                                 (59)

В силу формулы Тейлора, имеем

(60)

где ,

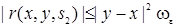
     при , причем .

Подставим (60) в (59), имеем:

         (61)

где  , когда и .

Разделим левую и правую части (61) на  , а затем, переходя к пределу  и , учитывая при этом непрерывность слагаемых правой части (61) по ,  получаем уравнение (58).

Покажем, теперь, . Действительно, из равенства   

в силу непрерывности функции получаем требуемое равенство. Доказательство закончено.

8.4. Предположим, что у переходной вероятности  существует плотность, т.е. существует функция   такая, что для   . Очевидно, что в этом случае соотношение Чепмена-Колмогорова для будет иметь вид

                                               (62),

где . Покажем теперь, что, если плотность  дифференцируема по t и дважды дифференцируема по y, то она удовлетворяет уравнению Фоккера-Планка-Колмогорова.

Теорема 13. Пусть условия (54)-(56) выполняются равномерно по x и существуют непрерывные производные

, где .

Тогда функция удовлетворяет уравнению Фоккера – Планка -

       (63)

Доказательство. Пусть  дважды дифференцируемая функция, равная нулю вне некоторого компакта. Аналогично доказательству теоремы 12 легко показать, что равномерно по x

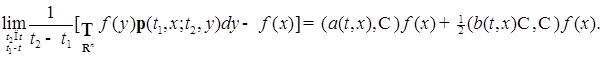
В силу условий теоремы и последнего равенства, имеем:

Вам также может быть полезна лекция "10.4 Жилище".

Рассмотрим теперь правую часть последнего равенства и заметим, что  равна нулю вне некоторого компакта, тогда в силу формулы интегрирования по частям, имеем

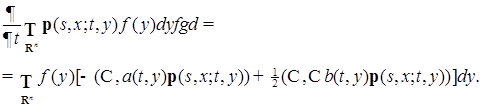
Из последнего равенства, имеем

                                    (64)

Утверждение теоремы следует из (64), в силу произвольности функции f(y).