Процессы с независимыми приращениями
§7 Процессы с независимыми приращениями.
7.1. Пусть E - линейное пространство, а 
-s-алгебра борелевских множеств на нем. Через
, где
, обозначим "параллельный" сдвиг множества B на вектор x, точнее: 
.
Пусть 
семейство вероятностных мер на 
удовлетворяющих условиям:
i) 
- -измеримая функция по x для 
;
ii) если 
, то справедливо равенство
(38)
Очевидно следующее равенство
(39)
Рекомендуемые материалы
Действительно. Если 
, то равенство (39) очевидно. Стало быть, (39) справедливо для простых функций, поэтому, в силу теоремы о монотонной сходимости, равенство (39) остается справедливым для любой измеримой ограниченной функции.
Из (38) следует равенство
(40)
Из (39) следует, что если положить 
, то 
- будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для 
Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то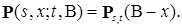 
7.2. Пусть q- вероятностная мера на 
и 
, где 
- вероятностная мера на 
, определенная формулой
(41)
причем 
где 
- переходная вероятность.
Определение. МПШ 
со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для 
N
, tk Î R+, 
t1<t2<…<tn , случайные вектора 
являются независимыми в совокупности, причем вектор 
- называется начальным значением процесса 
с распределением q, называемым начальным распределением.
Таким образом, чтобы задать процесс с независимыми приращениями достаточно знать:
а) начальное распределение вероятностей q случайного вектора,
б) распределение вероятностей случайных векторов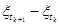 
.
Очевидно, что если заданы q и 
, то соотношение (41) определено совместное распределение векторов 
.
Покажем теперь, что введенное таким образом совместное распределение определяет процесс с независимыми приращениями. Действительно, пусть 
,где 
, и 
,тогда имеем:
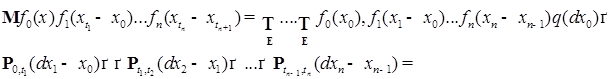
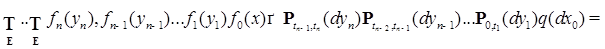
(42)
Отсюда следует независимость векторов. Стало быть, для процесса с независимыми приращениями справедливо равенство где любая 
для 
.
7.3. Процессы с независимыми приращениями (СПСП) удобно изучать с помощью характеристических функций. Пусть 
и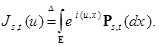 
Тогда из (42) следует, что
. (43)
Очевидно, (43) эквивалентно условию, что процесс 
является процессом с независимыми приращениями. Отсюда следует, что если 
и 
удовлетворяют (43), то справедливо равенство
(44)
где 
. Очевидно, что (44) эквивалентно тому, что - СПСП.
7.4. Определение. СПСП называется однородным (ОСПСП), если для любых 
- случайный вектор имеет распределение, не зависящее от t, т.е.
.
Определение. ОСПСП называется стохастически непрерывным, если он непрерывен по вероятности.
Приведем теперь некоторые свойства ОСПСП. Пусть 
, тогда справедливы следующие утверждения:
1) 
Это равенство вытекает из (43). Отсюда, в частности, следует, что 
.
2) Пусть - ОСПСП. Если 
,то для 
, такого что 
. Доказательство этого утверждения приведите самостоятельно.
3) 
. Действительно, пусть для любого 
существует 
такое, что 
для любых
. Пусть
. Из определения ОСПСП имеем
.
Так как для любого u, такого что
, 
, то существует такое 
(зависящее от N), что для любых t < tN 
. Стало быть, существует функция 
, т.е. 
. Отсюда в силу свойства 1) получаем что 
, для 
, и 
. Поэтому существует функция 
такая, что 
. Значит
, (44)
где 
можно определить следующим образом
=
,
причем сходимость равномерная по. Отсюда вытекает следующее свойство.
4) Для любых существует функция 
, называемая кумулянтой, такая что для любого
.
7.5. Теорема 10 (Леви-Хинчина). Пусть ОСПСП со значениями в 
стахостически непрерывный. Тогда существуют:
i) конечная мера П на 
ii) a - n – мерный вектор; iii) b - размера 
положительно определенная матрица,
такие что для любого 
такого, что кумулянта имеет вид: 
(46)
Замечание. В доказательстве теоремы 10 вместо формулы (46) удобнее воспользоваться следующей
(47)
где 
, 
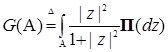
Доказательство. Пусть 
– распределение вероятностей процесса , а 
соответствующая ему характеристическая функция. Положим для 
B() 
. Предположим, что семейство мер 
- слабо компактно. Пусть 
- последовательность такая, что: a) 
при 
; б) 
слабо сходится к некоторой мере 
на B(). Тогда имеем
(48)
где 
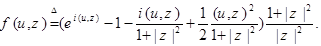
Так как 
, то 
- непрерывна и ограничена. Поэтому, в силу слабой сходимости 
к при , имеем
.
Значит, при 
и существуют пределы 
где 
- линейная функция, т.е. 
, а 
- положительно определенная квадратическая форма, т.е. 
, соответственно. Поэтому в (48) можно произвести предельный переход при 
, получим
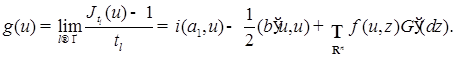
Пусть 
, где {0}- одноточечное множество, “состоящее” из точки “нуль”. Так как 
, то 
. Кроме того, интеграл
существует и представляет собой положительно определенную квадратическую форму по u, т.е. 
. Из приведенных построений следует, что 
. Поэтому существует положительно определенная матрица 
, такая что 
,
что и доказывает (47).
Установим слабую компактность семейства мер 
. В силу теоремы 36 главы 1 нужно установить, что: а) 
; б)
где 
.
Пусть 
, 
. В силу условий теоремы и (46), получаем, что для любого 
существует такое 
, что
, при 
(49)
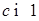
и при 
, при 
. (50)
Так как 
для 
, то из (49) следует, что
(51)
Нам понадобятся значения интегралов:
где Г(k) - Гамма-функция, 
- функция Бесселя, порядка m действительного аргумента. Проинтегрируем неравенства (49), (50) по 
, а затем получившийся результат разделим на 
, (
), имеем:
(52)
(53)
Рассмотрим (52), пусть 
и 
, имеем
.
Рассмотрим (53). Так как 
- ограничена, то можно выбрать (при любом c>0) 
таким, что
(54)
Тогда имеем 
.
Основы эмбриологии 2 - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Из вышеприведенных рассуждений следует, что 
, для любого t .
Заметим, что 
. Выберем теперь 
таким, что левая часть (52) не превосходила 
, а 
cтаким, чтобы выполнялось (54). Тогда получаем, что 
для любого t. Доказательство закончено.
7.6. Рассмотрим частные случаи формулы (47), когда n =1.
1) Пусть 
и 
для любого 
. В этом случае 
. Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке 
. Следовательно, 
, т.е. точка 
движется с постоянной скоростью а.
2) Пусть для любого. В этом случае приращения 
имеют нормальное распределение со средним 
и дисперсией равной 
. Если 
, то процесс 
является гауссовским. Отметим, что если 
и 
, то такой процесс называется винеровским.
3) Пусть 
и , а мера П сосредоточена в точке {1} и имеет в ней массу, равную единице. Тогда характеристическая функция будет иметь вид 
. Отсюда следует, что 
. Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3.
